На деякому етапі обробки заданої системи даних часто бажано буває спростити відповідні цій системі даних системи, що породжують.

Існує два основні методи одночасного спрощення систем даних і відповідних систем, що породжують:

1) спрощення за рахунок виключення деяких змінних з відповідної подібної системи;

2) спрощення за рахунок визначення класів еквівалентності станів деяких змінних.

 Хай безліч змінних тієї, що породжує системи V складається з п змінних і будь-якої підмножини V, за винятком порожньої множини, представляє змістовне спрощення першого роду. Отже, є нетривіальних спрощення першого роду. Вони частково впорядковані по відношенню «підмножина». Якщо для зручності включити початкову множину V і порожня множина, то безліч спрощень з частковим впорядкуванням утворює грати. Назвемо ці грати гратами змінних або V-гратами і позначимо . Зрозуміло, що V -решетка може бути описана або як

або як

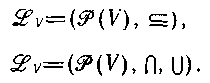 (4.88)

Позначимо через fB функцію поведінки заданої системи з поведінкою із змінними, що становлять множину V. При спрощенні цієї системи за допомогою скорочення множини V до підмножини нова (спрощена) функція поведінки fB визначається проекцією

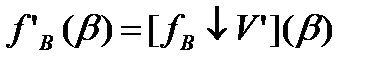(4.89)

визначеної рівнянням (4.57).

Скорочення другого роду зводяться до зменшення числа станів, що виділяються для окремих змінних. Одним із способів їх опису є визначення функції

 (4.90)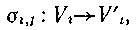

де - задана безліч станів (змінною ); - спрощена (скорочене) безліч станів тієї ж змінної; - новий стан, привласнений початковому стану, а - це ідентифікатори, за допомогою яких розрізняються різні функції вигляду (4.90), застосовані до безлічі станів однієї і тієї ж змінної. Якщо, то стани х і у ізпрі спрощенні виявляються невиразними. Функція (4.90) повинна бути голоморфна щодо всіх математичних властивостей початкової безлічі Vi, які вважаються істотними з погляду даного завдання. Будемо функцію (4.90), що є гомоморфізмом в описаному вище сенсі, називати спрощуючою функцією.

Будь-яка спрощуюча функція індукує розбиття на множині. Будь-яке розбиття складається з груп станів V,, які неотлічими при даному спрощенні. Таке розбиття (яке зберігає істотні властивості ) називатимемо вирішуючою формою.

Що вирішують форми, визначені на якійсь безлічі станів, можуть бути впорядковані за допомогою звичайного відношення уточнення, визначеного на розбитті даної множини. Добре відомо, що таке відношення уточнення є відношенням часткового порядку і утворює грати. Для двох заданого розбиття, скажемо X і У, визначених на одній і тій же множині, говоритимемо, що X є уточненим розбиттям Y тоді і тільки тоді, коли для будь-якої групи х з X існує група у з У, така, що . Якщо X, що уточнює розбиття У, то У називається укрупненим розбиттям X. Грати вирішуючих форм, визначених на безлічі станів, називатимемо вирішуючими гратами і позначати . Будь-які вирішуючі грати безлічі станів можуть бути визначені або у вигляді

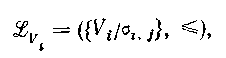 (4.91)

або у вигляді

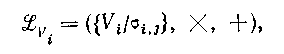 (4.92)

де і позначають відповідно твір і суму розбиття.

Якщо дана безліч станів не володіє математичними властивостями, які повинні бути збережені, то як вирішуюча форма прийнятно будь-яке розбиття.

В цьому випадку вирішуючі грати містять все розбиття, яке може бути визначені на цій безлічі станів. Якщо безліч станів складається з m станів, то число вирішуючих форм в гратах, визначається формулою

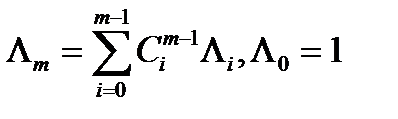 (4.93)

Нижче показано величезне число вирішуючих форм навіть для невеликого числа станів:

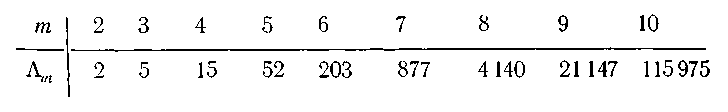
Оскільки найменша уточнена вирішуюча форма (всі стани в одному блоці) сенсу не має, а найбільше уточнення дає спрощення, те число осмислених спрощень рівне.

Якщо безліч станів повністю впорядкована і потрібно зберегти цю впорядкованість при спрощеннях, то число вирішуючих форм істотно менше за число, що задається формулою. Хай - це стани і . Тоді для будь-якого і або об'єднуються в одну групу чи ні. Тільки ці рішення визначають конкретне розбиття. Таким чином, для т станів приймається m-1 бінарне рішення. Отже, для повністю впорядкованої безлічі станів

 (4.94)

Очевидно, що ці грати для m станів ізоморфна булевим гратам для впорядкування підмножин будь-якої множини з m-1 елементу. У наступній таблиці приводяться значення, обчислені за формулою (3.94); в цьому випадку число вирішуючих форм істотно менше, ніж у разі неврегульованої безлічі станів: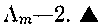

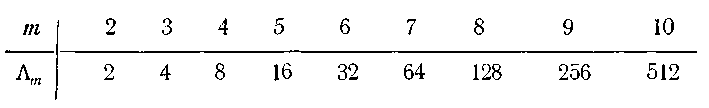
Число змістовних спрощень знову рівне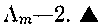

Приклад 4.7. Розглянемо змінну, станами якої є кольори світлофора: червоний, жовтий, зелений. Оскільки вони не впорядковані, все розбиття безлічі станів прийнятне як вирішуючі форми. Діаграма Хассе для цих грат приведена на мал. 4.13. Букви до, же, з означають відповідно червоний, жовтий і зелений кольори. Групам в окремих вирішуючих формах показані рисками над відповідними буквами. Стрілка на діаграмі указують напрям уточнення розбиття. Для спрощення початкової системи потрібно рухатися в напрямі, зворотному стрілкам.

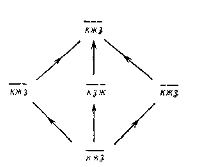
Мал. 4.13. Грати вирішуючих форм.

Якщо вибрано дещо змінних, то будь-яка вирішуюча форма для однієї змінної може бути об'єднана з будь-якою вирішуючою формою іншої змінної. Всі ці комбінації можна включити в одні грати, що представляють вибраний набір змінних. Називатимемо її об'єднаними вирішуючими гратами. Математично вона є твором окремих вирішуючих грат.

 Хай 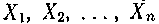- безліч елементів окремих вирішуючих грат вибраних змінних, а X - безліч елементів відповідних вирішуючих грат. Зрозуміло, що загальне число елементів об'єднаних вирішуючих грат рівне твору числа елементів окремих вирішуючих грат, тобто

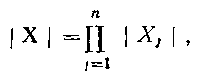 (4.95)

проте тільки деякі з них є змістовними спрощеннями. Зокрема, будь-яка комбінація, в яку входить найменша уточнена вирішуюча форма (розбиття на одну групу) однієї з вирішуючих грат, є безглуздою. Комбінація всіх найбільш уточнених вирішуючих форм також не представляє спрощення. Отже, загальне число елементів об'єднаних грат, що представляють змістовні спрощення, визначається по формулі

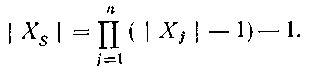 (4.96)

У окремому випадку, коли всі окремі грати однакові і кожна складається з вирішуючих форм, ми одержуємо

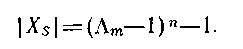 (4.97)

Більш того, якщо всі вирішуючі грати побудовані на повністю впорядкованій множині з т станами, то

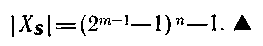 (4.98)

Вимоги, що спрощуючі породжують системи:

1) щоб системи були якомога простіші;

2) щоб ступінь нечіткості систем, що породжує, був якомога менше.

Називатимемо вимогу 1 вимогою простоти, а вимога 2 вимогою чіткості.

Щоб конкретизувати вимогу простоти для систем з поведінкою слід задати певну міру складності. Хай, наприклад, складність системи з поведінкою оцінюється числом реальних станів системи, тобто числом станів, що мають ненульову вірогідність або можливості. Це дуже проста міра, але, можливо, найбільш змістовна.