Математический аппарат построения математических

Моделей

Как отмечено выше, в зависимости от степени детализации рассматриваемого объекта теоретическое исследование его физической сущности, явлений и процессов, в нем возникающих, осуществляют методом математического моделирования на микро-, макро- и метауровне.

Теоретическое исследование на микроуровне направлено на изучение явлений и процессов, возникающих и протекающих в точках сплошной среды в результате взаимодействия с ней объектов окружающей среды. Например, при механической обработке резанием существенно изменяются физико-механические свойства материала поверхностного слоя обрабатываемых деталей: твердость, пластичность, сопротивление усталости и др. Изменение этих свойств обусловлены преобразованием механической энергии сил резания в тепловую энергию с развитием тепловых явлений в некотором объеме материала поверхностного слоя.

Математическое моделирование на микроуровне выполняют с использованием математического аппарата таких технических наук, как теория упругости, теория пластичности, теплофизика механической обработки и др. Математический аппарат этих наук составляют дифференциальные уравнения с частными производными различного порядка. Это уравнения Ламе, описывающие напряжённо-деформированное состояние деталей, уравнения теплопроводности, отражающие процесс распространения теплоты в объекте, уравнения электродинамики и др. В них независимыми переменными являются время и координаты точек сплошной среды, в которых определяются параметры исследуемого процесса (температура, напряжения, деформация и т. п.).

В частности, в теплофизике механической обработки при разработке математической модели процесса теплообмена между компонентами технологической системы используется уравнение теплопроводности вида

,

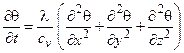в котором: λ - коэффициент теплопроводности материала среды; c_v – объемная теплоемкость среды.

Это уравнение отражает изменение во времени t температуры θ(x, y , z , t) в рассматриваемой точке с координатами (x, y , z) сплошной теплопроводящей среды.

Теоретическое исследование на макроуровне направлено на изучение явлений и процессов, возникающих и протекающих в элементах сложного объекта при их взаимодействии между собой и взаимодействии самого объекта с объектами окружающей среды. При этом изучаемый объект рассматривается как некоторая система, к которой применимы методы анализа и синтеза. Изучение системы осуществляется методом структурного моделирования с построением модели структуры этой системы.

Модель структуры системы представляет собой модель состава элементов системы, дополненная информацией о связях между ними, которые принято называть отношениями между элементами. Эти отношения могут отражать взаимное расположение элементов, взаимовлияние физических процессов, протекающих в элементах системы (силовых, тепловых и т. п.), взаимосвязи свойств т. д.

В соответствии с целями исследования в ходе анализа системы строится (или выбирается) математическая модель для каждого элемента, входящего в систему. Она представляет собой уравнение (алгебраическое или дифференциальное), которое описывает функцию (назначение) рассматриваемого элемента. Например, при исследовании технических систем (механических, электрических, гидравлических и др.) на макроуровне выделяют три типа их простейших элементов:

· элемент типа R – элемент диссипации (уменьшения) энергии. На этом элементе, как правило, происходит преобразование энергии в тепловую.

· элемент типа С. На этом элементе происходит накопление потенциальной энергии (механической, электрической и др.)

· элемент типа L, на котором происходит накопление кинетической энергии.

Математические модели простейших элементов механической поступательной системы приведены в таблице 1.

Таблица 1. Элементы механической поступательной системы и их математические модели

Тип элемента	Название элемента	Условное графическое обозначение	Характеристика элемента	Математическая модель
Механическая поступательная система
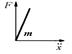
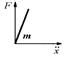
R	Элемент вязкого трения
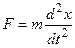
C	Элемент массы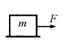
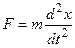
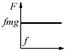
	Элемент сухого трения
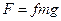
L	Упругий элемент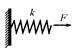

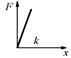
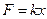
Созданные в ходе анализа математические модели отдельных элементов объекта макроуровня позволяют построить полную ММ этого объекта как единого целого. Математические модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений. Эти уравнения отражают состав элементов системы, законы их функционирования, характер их объединения и взаимосвязи, которые устанавливаются между элементами в результате синтеза последних в систему, как единое целое.

На метауровне рассматриваются сложные объекты – системы, которые представляют собой сложную совокупность взаимодействующих между собой элементов, например, в машиностроении это металлорежущие станки, приспособления, рабочие участки механического цеха, цех в целом и т. п. Моделирование таких объектов осуществляют с использованием методов системного анализа. Это методы теории случайных процессов, теории марковских процессов, эвристического программирования, теории информации.

Математические модели на метауровне представляют собой системы обыкновенных дифференциальных уравнений, системы логических уравнений, системы дифференциальных уравнений Колмогорова и др.

В качестве примера моделирования на метауровне рассмотрим техническое устройство S, состоящее из двух узлов, и которое может находиться в одном из четырех состояний (рисунок 3):

S₀ – оба узла исправны;

S₁ – первый узел ремонтируется, второй исправен;

S₂ –второй узел ремонтируется, первый исправен;

S₃ –оба узла ремонтируются.

Переход устройства из i -го состояния в j -е происходит вследствие воздействия на него потока λ случайных событий (например, изменение температуры, появление вибрации основания и т. п.), вызывающие возникновение неисправностей того или иного узла. Обозначив интенсивности потоков событий, переводящих систему из i -го состояния в j -е состояние через λ_ij, получим граф состояний, приведенный на рисунке 3.

Полагая, что в рассматриваемый момент времени t вероятность того, что устройство может находиться в состоянии S₀ или S₁, или S₂, или S₃ соответственно равна p₀(t), p₁(t), p₂(t), p₃(t). Тогда, на основе понятий марковского случайного процесса математическая модель изменения состояний устройства во времени запишется в виде системы уравнений Колмогорова

с четырьмя неизвестными функциями вероятностей от времени p₀(t), p₁(t), p₂(t), p₃(t).

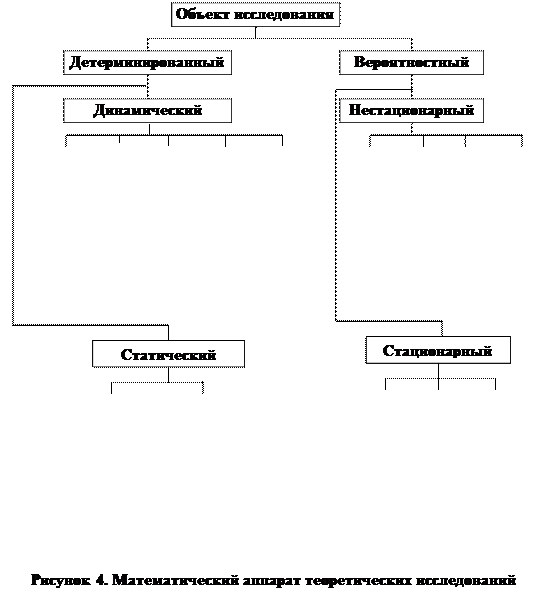
В целом выбор математического аппарата для построения модели определяется видом объекта исследования - детерминированный или вероятностный, динамический или статический, нестационарный или стационарный и поставленными целями его исследования (рисунок 4).