Лекция 2
2018/2019 уч. г.
Тема 5. Теоретические исследования
Лк – 0,5 час. ПЗ – 2 час. СРС 3 час.
1. Цель и задачи теоретических исследований.
2. Основы системного подхода в теоретических исследованиях.
2.1. Принципы системного подхода.
2.2. Понятие системы. Анализ и синтез систем.
3. Математический аппарат теоретических исследований.
3.1. Математический аппарат построения математических моделей.
3.2. Методы решения математических моделей.
Тема 6. Моделирование объектов в научных исследованиях
Лк – 0,5 час. ПЗ – 2 час. СРС 3 час.
1. Основные понятия и определения метода моделирования объекта исследования.
1. Элементы теории размерностей.
2. Основные понятия теории подобия.
3. Математическое моделирование объекта исследования.
3.1. Предназначение моделей.
3.2. Этапы построения и реализации математической модели объекта исследования.
Тема 7. Постановка научной проблемы.
Этапы научно-исследовательской работы
Лк – 1,0 час. ПЗ – 0 час. СРС 3 час.
1. Направления научного исследования. Структурные элементы научного направления.
2. Постановка научно-технической проблемы.
3. Оценка экономической эффективности темы научных исследований.
4. Этапы научно-исследовательской работы.
5. Объект и предмет исследования, параметры и факторы объекта.
6. Разработка рабочей гипотезы.
Литература (основная)
1. Горелов Н. А. Методология научных исследований: учебник для бакалавриата и магистратуры / Н.А. Горелов, Д. В. Круглов. М.: Издательство Юрайт, 2014. -290 с.
2. Основы научных исследований: Учебник для вузов / под ред. В. Г. Кучерова / ВолгГТУ. Волгоград, 2004.
3. Основы научных исследований: Учеб. для техн. вузов / В.И. Крутов, И.М. Грушко, В.В. Попов и др.; Под ред. В. И. Крутова, В.В. Попова. – М.: Высш. шк., 1989. – 400 с.
Основы системного подхода в теоретических исследованиях
Принципы системного подхода
Проведение теоретических исследований осуществляется с использованием общенаучных методов анализа и синтеза, индукции и дедукции, аналогии, моделирования и др., которые объединяются под названием «общая теория систем» или «системология» [3]. Широкое применение в теоретических исследованиях получил системный подход, который включает в себя ряд принципов общей теории систем, в частности, принцип системности, принцип иерархичности, принцип формализации и системный анализ.
Принцип системности гласит, что при изучении объекта его следует рассматривать как целостное образование, т. е. как систему.
Согласно принципу иерархичности каждый объект должен рассматриваться на трех уровнях: изучение самого объекта, изучение объекта в качестве элемента более общей системы (объект - подсистема), изучение объекта в соотношении с составляющими его элементами (объект - надсистема).
В соответствии с принципом формализации системный подход нацелен на получение количественных характеристик систем, разработку методов описания, анализа и синтеза систем.
Системный анализ включает в себя следующие основные методы исследования систем: эвристическое программирование, методы аналогии, аналитические методы и моделирование.
Эвристическое программирование основывается на результатах анализа деятельности человека, решающего сложную задачу со значительной степенью неопределенности. Основу эвристического программирования составляет группа методов экспертных оценок - метод Дельфи, Цвикки, мозговой атаки и др. [1].
Методы аналогии используются при исследовании сложных систем по каким-то отдельным характеристикам, сводя их к известным хорошо изученным процессам (течение идеального газа, диффузионные процессы и т. п.), а также путем переноса знаний о каком-либо объекте, в т. ч. биологическом, на исследуемый, сходный с ним по существенным свойствам и качеству.
Аналитические методы системного анализа весьма разнообразны. Это теория принятия решений, теория графов, метод «черного ящика» и др.
Моделирование является одним из основных методов и применяется на эмпирическом и теоретическом уровнях исследования объектов и явлений, их состояний и поведения. Моделирование позволяет вскрыть качественные и количественные свойства изучаемых явлений как одинаковой с их моделью физической природы, так и разнородной физической сущности. В системном анализе наибольшее применение получило имитационное моделирование, в котором осуществляется процесс создания математической модели изучаемого объекта и выполнения с помощью ЭВМ вычислительного эксперимента на этой модели с целью выявления свойств системы, путей ее создания, совершенствования и использования.
Моделей
Как отмечено выше, в зависимости от степени детализации рассматриваемого объекта теоретическое исследование его физической сущности, явлений и процессов, в нем возникающих, осуществляют методом математического моделирования на микро-, макро- и метауровне.
Теоретическое исследование на микроуровне направлено на изучение явлений и процессов, возникающих и протекающих в точках сплошной среды в результате взаимодействия с ней объектов окружающей среды. Например, при механической обработке резанием существенно изменяются физико-механические свойства материала поверхностного слоя обрабатываемых деталей: твердость, пластичность, сопротивление усталости и др. Изменение этих свойств обусловлены преобразованием механической энергии сил резания в тепловую энергию с развитием тепловых явлений в некотором объеме материала поверхностного слоя.
Математическое моделирование на микроуровне выполняют с использованием математического аппарата таких технических наук, как теория упругости, теория пластичности, теплофизика механической обработки и др. Математический аппарат этих наук составляют дифференциальные уравнения с частными производными различного порядка. Это уравнения Ламе, описывающие напряжённо-деформированное состояние деталей, уравнения теплопроводности, отражающие процесс распространения теплоты в объекте, уравнения электродинамики и др. В них независимыми переменными являются время и координаты точек сплошной среды, в которых определяются параметры исследуемого процесса (температура, напряжения, деформация и т. п.).
В частности, в теплофизике механической обработки при разработке математической модели процесса теплообмена между компонентами технологической системы используется уравнение теплопроводности вида
,
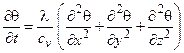в котором: λ - коэффициент теплопроводности материала среды; cv – объемная теплоемкость среды.
Это уравнение отражает изменение во времени t температуры θ(x, y , z , t) в рассматриваемой точке с координатами (x, y , z) сплошной теплопроводящей среды.
Теоретическое исследование на макроуровне направлено на изучение явлений и процессов, возникающих и протекающих в элементах сложного объекта при их взаимодействии между собой и взаимодействии самого объекта с объектами окружающей среды. При этом изучаемый объект рассматривается как некоторая система, к которой применимы методы анализа и синтеза. Изучение системы осуществляется методом структурного моделирования с построением модели структуры этой системы.
Модель структуры системы представляет собой модель состава элементов системы, дополненная информацией о связях между ними, которые принято называть отношениями между элементами. Эти отношения могут отражать взаимное расположение элементов, взаимовлияние физических процессов, протекающих в элементах системы (силовых, тепловых и т. п.), взаимосвязи свойств т. д.
В соответствии с целями исследования в ходе анализа системы строится (или выбирается) математическая модель для каждого элемента, входящего в систему. Она представляет собой уравнение (алгебраическое или дифференциальное), которое описывает функцию (назначение) рассматриваемого элемента. Например, при исследовании технических систем (механических, электрических, гидравлических и др.) на макроуровне выделяют три типа их простейших элементов:
· элемент типа R – элемент диссипации (уменьшения) энергии. На этом элементе, как правило, происходит преобразование энергии в тепловую.
· элемент типа С. На этом элементе происходит накопление потенциальной энергии (механической, электрической и др.)
· элемент типа L, на котором происходит накопление кинетической энергии.
Математические модели простейших элементов механической поступательной системы приведены в таблице 1.
Таблица 1. Элементы механической поступательной системы и их математические модели
| Тип элемента | Название элемента | Условное графическое обозначение | Характеристика элемента | Математическая модель |
| Механическая поступательная система | ||||
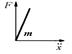
| R | Элемент вязкого трения | 
| 
| 
|
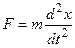
| C | Элемент массы |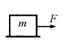 
| 
|
|
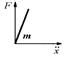
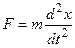
| Элемент сухого трения | 
| 
|  
| |
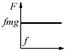
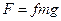
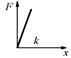
| L | Упругий элемент |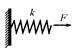 
| 
| 
|
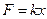
Созданные в ходе анализа математические модели отдельных элементов объекта макроуровня позволяют построить полную ММ этого объекта как единого целого. Математические модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений. Эти уравнения отражают состав элементов системы, законы их функционирования, характер их объединения и взаимосвязи, которые устанавливаются между элементами в результате синтеза последних в систему, как единое целое.
На метауровне рассматриваются сложные объекты – системы, которые представляют собой сложную совокупность взаимодействующих между собой элементов, например, в машиностроении это металлорежущие станки, приспособления, рабочие участки механического цеха, цех в целом и т. п. Моделирование таких объектов осуществляют с использованием методов системного анализа. Это методы теории случайных процессов, теории марковских процессов, эвристического программирования, теории информации.
Математические модели на метауровне представляют собой системы обыкновенных дифференциальных уравнений, системы логических уравнений, системы дифференциальных уравнений Колмогорова и др.
В качестве примера моделирования на метауровне рассмотрим техническое устройство S, состоящее из двух узлов, и которое может находиться в одном из четырех состояний (рисунок 3):
S0 – оба узла исправны;
S1 – первый узел ремонтируется, второй исправен;
S2 –второй узел ремонтируется, первый исправен;
S3 –оба узла ремонтируются.
Переход устройства из i -го состояния в j -е происходит вследствие воздействия на него потока λ случайных событий (например, изменение температуры, появление вибрации основания и т. п.), вызывающие возникновение неисправностей того или иного узла. Обозначив интенсивности потоков событий, переводящих систему из i -го состояния в j -е состояние через λij, получим граф состояний, приведенный на рисунке 3.
Полагая, что в рассматриваемый момент времени t вероятность того, что устройство может находиться в состоянии S0 или S1, или S2, или S3 соответственно равна p0(t), p1(t), p2(t), p3(t). Тогда, на основе понятий марковского случайного процесса математическая модель изменения состояний устройства во времени запишется в виде системы уравнений Колмогорова
с четырьмя неизвестными функциями вероятностей от времени p0(t), p1(t), p2(t), p3(t).
В целом выбор математического аппарата для построения модели определяется видом объекта исследования - детерминированный или вероятностный, динамический или статический, нестационарный или стационарный и поставленными целями его исследования (рисунок 4).
               |
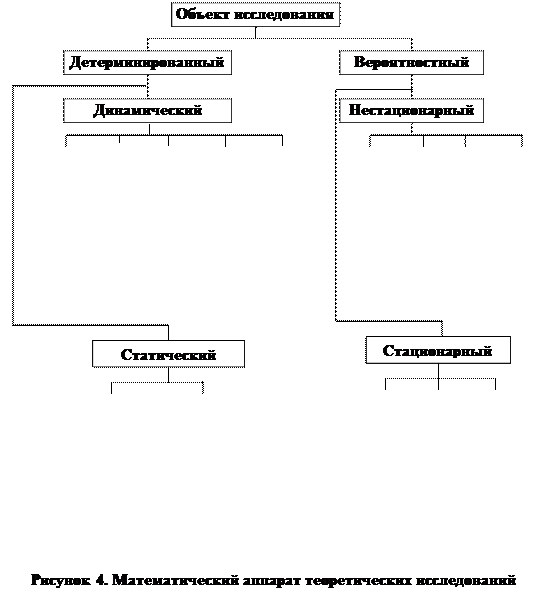Объекта исследования
Моделирование определяют как метод практического или теоретического опосредованного оперирования объектом. При этом исследуется не сам объект, а его модель, находящаяся в некотором объективном соответствии с самим познаваемым объектом и способная на отдельных этапах познания представлять в определенных отношениях изучаемый объект, а также давать по результатам ее исследования информацию об объекте [2,4].
В самом общем случае, независимо от предметной области деятельности человека под моделью понимают такой материальный или в иной форме представляемый объект, который в процессе познания (изучения) заменяет объект-оригинал, сохраняя некоторые важные с точки зрения поставленных целей применения типичные его черты.
Согласно определению, модель может представлять собой устройство, воспроизводящее строение или действие реального устройства, аналог в виде чертежа, графика, схемы, описания в вербальной, табличной, математической или иной форме представления.
Исходя из предназначения модели, как носителя свойств объекта-оригинала, она сама должна обладать следующими свойствами:
· полнотой, т. е. полнотой учета свойств, поведения объекта-оригинала;
· адекватностью, т. е. способностью отображать учитываемые свойства или поведение оригинала с погрешностью не выше заданной величины;
· простотой. Естественно, что из двух адекватных моделей, позволяющих достичь поставленную цель, предпочтение должно быть отдано более простой. При этом адекватность и простота модели далеко не всегда являются противоречивыми свойствами;
· потенциальностью, т. е. предсказательностью с точки зрения возможности получения новых знаний об исследуемом объекте. Другими словами, модель должна содержать в себе знания, которые человек не знает при создании модели, но может их приобрести в процессе использования модели (например, периодическая таблица Д. И. Менделеева химических элементов);
· и др. (экономичностью, наглядностью и т. п.).
 |
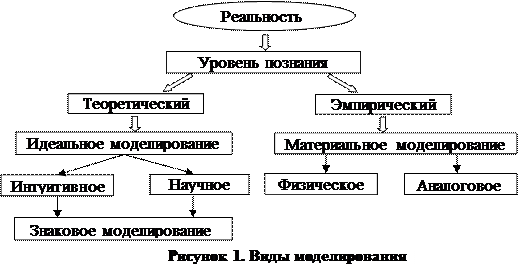Процесс построения и использования модели называется моделированием. В соответствии с тем, на котором уровне (эмпирическом или теоретическом) осуществляется моделирование, условно выделяют материальное и идеальное моделирование (рисунок 1).
Материальное моделирование – это моделирование, при котором исследование объекта выполняется с использованием его материального аналога, воспроизводящего основные физические, геометрические, динамические и функциональные характеристики данного объекта. Выделяют две разновидности материального моделирования: физическое (натурное) моделирование и аналоговое.
Физическое моделирование – это изучение реального объекта на его геометрически подобной материальной модели (увеличенной или уменьшенной), в которой реализуется такой же по физической природе процесс, что и в объекте-оригинале с последующим перенесением полученных на модели результатов на реальный объект на основе положений теории подобия.
Аналоговое моделирование – это изучение реального объекта на материальной модели, в которой реализуется иной по физической природе процесс по отношению к процессу в объекте-оригинале, но имеющий такое же математическое описание, как и процесс в реальном объекте.
Идеальное моделирование отличается от материального тем, что оно основано не на материальной аналогии объекта и модели, а на аналогии идеальной, мыслимой, т. е. в сознании исследователя создается определенный образ объекта, его идеальная модель, не содержащая ненужных с точки зрения целей исследования признаков, свойств. Идеальное моделирование разделяют на два вида: интуитивное и научное моделирование.
Интуитивное моделирование – это моделирование, основанное на непосредственном без логического обоснования какими-то доказательствами, чувственном представлении той или иной модели объекта. Исходной базой интуитивного моделирования являются знания и умения, накопленные многовековым опытом и передающиеся от поколения к поколению.
Научное моделирование – это логически обоснованное моделирование, использующее минимальное число предположений, принятых в качестве гипотез на основании результатов наблюдений за объектом моделирования. Главное отличие научного моделирования от интуитивного заключается не только в умении выполнять необходимые операции и действия по собственно моделированию, но и в знании «внутренних» механизмов, которые необходимо использовать при заданных целях моделирования.
Знаковое моделирование. Знаковым называют моделирование, использующее в качестве моделей знаковые изображения какого-либо вида: схемы, графики, чертежи и т. п., включающие также совокупность законов и правил, по которым можно оперировать с выбранными знаковыми образованиями и элементами. Одним из видов знакового моделирования является математическое моделирование.
Математическое моделирование – это идеальное научное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов. Построенная при моделировании математическая модель представляет собой систему математических объектов – чисел, переменных, векторов, множеств, функций, уравнений и т. п. и отношений между ними, отражающих важнейшие свойства исследуемого объекта.
Однако при моделировании, как на эмпирическом, так и на теоретическом уровне всегда должны использоваться определенные соотношения, определяющие условия перехода от модели к исследуемому объекту (оригиналу). Такие соотношения устанавливаются на основе теории подобия и принципа размерности [4, 6, 7].
Основные понятия теории подобия
Выше было отмечено, что при моделировании изучаемых явлений обязательным является использование определенных соотношений, определяющих условия перехода от модели к исследуемому объекту (оригиналу). Такие соотношения устанавливаются на основе теории подобия и принципа размерности. Особая ценность теории подобия заключается в том, что она позволяет получить при моделировании объектов обоснованно обобщенные выводы и установить строгие границы их применения.
Подобие явлений характеризуется соответствием (в частном случае пропорциональностью) величин, участвующих в описании изучаемых явлений, происходящих в оригиналах и моделях. По степени соответствия параметров модели и оригинала выделяют следующие виды подобия.
Абсолютное подобие. Представляет собой абстрактное понятие, реализуемое только умозрительно, поскольку это понятие требует полное тождество состояний или явлений в пространстве и времени.
Полное подобие. Это подобие таких процессов, протекающих во времени и пространстве, которые достаточно полно для поставленных целей данного исследования определяют изучаемое явление.
Неполное подобие. Этот вид подобия используется при изучении процессов только во времени или только в пространстве. Так, электромеханические процессы в синхронном генераторе могут быть подобны во времени, без соблюдения геометрического подобия полей внутри машины (т. е. подобия в пространстве).
Приближенное подобие. Реализуется при некоторых упрощающих допущениях, приводящих к искажениям, заранее оцениваемым количественно.
Примеры моделирования при полном, неполном и приближенном моделировании приведены в работе [4].
Гениальное предвидение науки о подобии явлений было высказано Ньютоном во II – й его книге «Principia[1]» в 1686 г., который изложил принципы механического, кинематического и динамического подобий. Но только в 1848 г. член французской академии наук Жозеф Бертран впервые установил основное свойство подобных явлений, сформулировав первую теорему подобия, теорему о существовании инвариантов (критериев) подобия. Эта первая теорема подобия была сформулирована для механических явлений. Согласно этой теореме в природе существуют только те подобные явления, у которых критерии одинаковы.
Вторая теорема подобия устанавливает возможность преобразования физических уравнений, отражающих взаимосвязи между характеристиками объектов, в форму критериальных уравнений. Эта теорема была выведена русским ученым А. Федерманом в 1911 г. и несколькими годами позже, в 1914 г., американским ученым Букингэмом (Buckingham J.).
Первая и вторая теоремы устанавливают свойства подобных явлений, но не указывают, по каким признакам можно установить, что явления подобны. Ответ на этот вопрос дается третьей теоремой подобия, доказательство которой было выполнено М. В. Кирпичевым в 1930 г.
Все три теоремы являются базой современной теории подобия, отражающей общие закономерности подобия явлений и процессов.
Из геометрии известно. что подобные фигуры обладают свойством равенства соответствующих углов и равенства отношения сходственных сторон одному и тому же постоянному числу. именуемому масштабным коэффициентом (или просто масштабом) подобия n
,
где 
, 
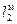и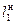 
, 
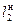- сходственные линейные размеры двух подобных фигур (условно модели – «м» и натуры – «н»).
Понятие подобия может быть распространено на любые физические явления при выполнении условия, что все величины, характеризующие рассматриваемое явление, например, плотность ρ, температура t, скорость v и др., должны быть подобными, т. е. для них должны иметь место следующие соотношения:
; 
; 
,
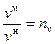где величины nρ , nt, nv – являются константами подобия.
Константы подобия для сложных физических явлений, характеризуемыми многими величинами, не могут быть выбраны произвольно, поскольку между этими величинами существуют определенные связи. Например, для сходственных частиц подобных тел скорость их движения составляет:
для первого тела (натуры)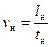 
и для второго (модели) 
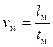, где скорость v равна отношению пути l, пройденного частицей тела за промежуток времени t, к этому промежутку времени.
Разделив почленно два написанных равенства одно на другое, получим
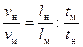. (1)
На основании определения подобия имеем следующие соотношения:
; 
; 
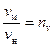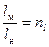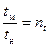. (2)
Подставляя в уравнение (1) вместо отношения величин их константы подобия, находим
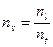или 
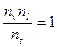. (3)
Наряду с этим из (1) после группирования величин с индексом «м» и «н» получим
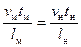. (4)
Члены последнего уравнения являются безразмерными объединениями величин, характеризующих различные стороны рассматриваемого явления. Для подобных явлений эти объединения сохраняют одно и то же числовое значение, т. е. для рассматриваемого случая можем записать
.
Такие безразмерные объединения (комплексы) величин называются критериями подобия и обозначаются через πi. Помимо выше приведенного, это могут быть
; 
; 
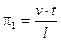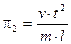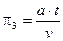и т. д.
Такие критерии получают из анализа уравнений, описывающих рассматриваемые процессы или явления (обычных алгебраических таких как, например, для скорости, мощности и т. п., а также более сложных, в т. ч. дифференциальных). Более того, критерии подобия можно составить и при отсутствии аналитической зависимости между исследуемыми величинами. В этом случае используется теория размерностей [2, 4].
Правила перехода при моделировании от модели к оригиналу при их подобии базируются на трех теоремах подобия.
Содержание первой теоремы теории подобии определяет достаточное условие подобия двух объектов (модели и оригинала), которое должно быть соблюдено при установлении связей между величинами, характеризующими различные свойства, поведение и др. стороны этих объектов.
Теорема 1. Подобные между собой объекты имеют одинаковые критерии подобия.
Согласно этой теореме, чтобы модель и оригинал были подобны, необходимо выбрать S определяющих параметров, включая в них при необходимости характеристики начальных и граничных условий. Из этих параметров можно составить (S - r) независимых критериев подобия, где r – число принятых в рассматриваемом случае основных единиц измерения. При этом для всех составленных критериев подобия πi должно соблюдаться условие:
, где i = 1, 2, 3, …, (S - r).
См., например, уравнение (4).
Теорема 2 (π-теорема). Эта теорема гласит: «чтобы данные, полученные из опыта, можно было бы непосредственно распространить на подобные явления, их необходимо представить в виде зависимостей между критериями подобия», т. е. зависимостей вида
.
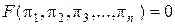Зависимости такого вида называются критериальными уравнениями.
Использование таких уравнений позволяет не только распространить результаты исследования модели на оригинал, но и значительно уменьшить количество величин, непосредственно участвующих в экспериментальном или теоретическом исследовании. Поскольку критерии подобия являются безразмерными, упрощается нахождение зависимостей между величинами, характеризующими изучаемый объект.
Теорема 3. Эта теорема определяет признаки подобия объектов. Она утверждает: «Подобны те явления, условия однозначности которых подобны, а составленные из условий однозначности критерии подобия численно равны». Вспомним, что под условиями однозначности понимают дополнительные условия, которые в совокупности с дифференциальным уравнением однозначно определяет единичное явление. К условиям однозначности в самом общем случае относятся: геометрические параметры изучаемого объекта (форма, размеры), механические и физические свойства, начальные условия, условия на граничных поверхностях объекта и др.
В частности, при исследовании процесса резания при обработке точением к условиям однозначности относятся следующие данные [5]:
1) геометрические характеристики резца (α, γ, φ, φ1, r,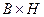 
,…), размеры среза и детали;
2) теплофизические и механические свойства обрабатываемого и инструментального материала (λ, cρ, σв, E,…);
3) граничные условия, к которым относятся принимаемые законы распределения напряжений, интенсивностей тепловых потоков и другие факторы, действующие на граничных поверхностях рассматриваемых объектов;
4) начальные условия, которые в зависимости от исследуемого процесса (теплового, механического – силового и т. п.) могут отражать распределение температуры, напряжений, перемещений и т. д. в начальный момент времени.
Пример. Поставлена задача моделирования перемещения x в моменты времени t груза массой m, который колеблется на пружине в вязкой среде, силы сопротивления которых равны: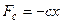 
; 
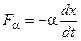, где c – жесткость пружины, Н/м; α – коэффициент вязкого трения, Н/(м/с), x - величина перемещения груза в момент времени t, (м).
Груз в момент времени t = t0, вследствие приложения ударной нагрузки, начал движение с начальной скоростью v0.
Известно, что математическая модель движения груза для заданных в задаче условий имеет вид дифференциального уравнения
с начальными условиями:
; 
.
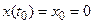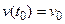Является очевидным, что перемещение x груза является функцией величин m, c, α, t, v
.
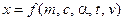Полагаем, что изучение колебательного движения груза в реальном объекте будет осуществляться на модели одинаковой с оригиналом физической природой. Следовательно, движение тела в объекте – оригинале и в его модели будут описываться соответственно уравнениями:
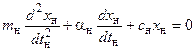; (5)
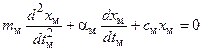, (6)
в которых индексами «н» и «м» обозначены величины, с помощью которых описано колебательное движение груза в оригинале и его материальной модели соответственно.
Для установления критериев подобия, прежде всего, введем константы подобия:
для перемещения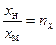 
;
для времени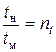 
;
для массы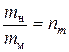 
для жесткости пружины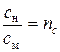 
;
для коэффициента вязкого трения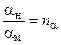 
;
для скорости 
.
Поскольку параметр x является функцией ряда величин, отражающих различные стороны исследуемого объекта (свойства отдельных элементов, время и др.), то выбор значений констант подобия не может быть произволен. Он определяется связями и отношениями, которые существуют между параметром x и этими величинами.
Размерности всех членов уравнений (5) и (6) одинаковы, знак дифференциала не влияет на размерность. Поэтому, опустив знаки дифференцирования, можем поделить все члены уравнений (5) и (6) на их первый член соответственно. В результате получим по два безразмерных комплекса величин для оригинала и модели:
; 
; 
; 
.
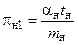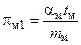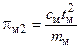Согласно первой теореме подобия, для подобных объектов полученные комплексы (критерии подобия) должны быть одинаковыми (idem), т. е.
; 
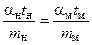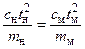. (7)
Условия (7) принято записывать в виде
; 
.
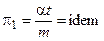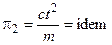Для определения условий выбора значений констант подобия подставим в равенства (7) вместо величин x, m, c, α, t их выражения через константы подобия, т. е. mн = nmmм, cн = nccм, αн = nααм, tн = nttм. Получим
; 
.
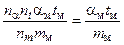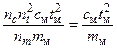Отсюда получаем условия выбора констант подобия
; 
.
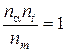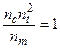Кроме того, согласно третьей теореме подобия, должно соблюдаться подобие условий однозначности. В нашем случае должно соблюдаться подобие начальных условий, т. е.
; 
.
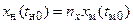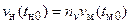Так как 
и 
, то, поделив почленно эти равенства одно на другое, получим еще один критерий подобия
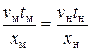, т. е. 
.
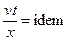Из последнего равенства находим еще одно условие выбора констант подобия
.
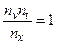Предназначение моделей
Наиболее распространенно применение моделей для изучения конкретных явлений и объектов - какова их структура, какие связи существуют между их элементами, какими свойствами обладают элементы и объект в целом, как они взаимодействуют с окружающей средой, законы развития и т. п.
Это обусловлено рядом причин, в частности тем, что некоторые объекты и явления вообще не могут быть изучены непосредственно или экспериментальное их исследование требует весьма больших финансовых затрат или рискованно для человека и/или среды его обитания.
Второе направление использования моделей составляют модели для приобретения знаний и умений по управлению объектом или процессом, определения наилучших способов управления при заданных целях и критериях. Такое направление использования моделей вполне объяснимо, прежде всего, с экономической точки зрения. Например, получить навыки в управлении современным самолетом безопаснее, быстрее и дешевле на тренажере (т. е. модели), чем подвергать себя и дорогую машину риску. Кроме того, любая модель, конечно, не обладает всеми свойствами реального объекта и в этом отношении модель «беднее» объекта-оригинала. В то же время хорошая модель «богаче» реального объекта по предоставляемым исследователю возможностям изучения сложного объекта. Модель позволяет экспериментировать с ней: вводить новые связи между элементами объекта или изменять существующие, изменять свойства элементов и т. п., чтобы понять физическую или иную сущность объекта, его возможности и т. д.
Третье направление использования моделей – это решение задач прогнозирования состояний объекта, прямых и косвенных последствий при реализации тех или иных способов и форм воздействий на объект и его отдельные элементы.
Например, при разработке технологических процессов изготовления деталей, составляющих узлы трения машин и механизмов, желательно уметь прогнозировать изменение надежности функционирования таких узлов в зависимости от методов обработки рабочих поверхностей пар трения.
Объекта исследования
Необходимость создания математической модели может быть связана с проектированием новых изделий, технологических процессов, созданием систем автоматического управления, планирования и контроля, проведением научных исследований. Процесс разработки математической модели трудоемок и связан с привлечением специалистов как в области, в которой возникла задача моделирования, так и в области прикладной математики, численных методов и программирования для ЭВМ.
Решение о создании математической модели принимает специалист той предметной области, в которой возникла проблема исследования объекта – явления, процесса, механизма и т. п. Его принято называть заказчиком. Исполнителем обычно выступает рабочая группа, включающая специалистов разного профиля – математиков, технологов, конструкторов и др.
Вопросы, которые обычно ставят заказчики, например, в области конструкторско-технологической подготовки машиностроительных производств - это вопросы повышения производительности обработки заготовок, увеличения стойкости режущего инструмента, вопросы, связанные с качеством обработки деталей и др. Подготовку списка вопросов, на которые должна ответить новая математическая модель, осуществляет один из специалистов рабочей группы. Его принято называть постановщиком задачи.
Непосредственной постановке задачи моделирования предшествует этап обследования, который включает следующие работы:
· обследование самого объекта моделирования с целью выявления основных факторов, механизмов, влияющих на его состояние, поведение, определение параметров, позволяющих описывать моделируемый объект;
· сбор и проверка имеющихся экспериментальных данных об объектах-аналогах, проведение при необходимости дополнительных экспериментов;
· 
аналитический обзор литературных источников, анализ и сравнение между собой построенных ранее моделей данного объекта или подобных ему объектов;
· анализ и обобщение всего накопленного материала, разработка общего плана создания математической модели.
На основе результатов обследования объекта моделирования постановщик задачи совместно с заказчиком формулирует содержательную постановку задачи моделирования, которая в дальнейшем, в процессе разработки модели, может уточняться и конкретизироваться.
Процесс построения и реализации математической модели объекта исследования включает в себя последовательность этапов, приведенных на рисунке 2. Рассмотрим краткое содержание работ, выполняемых на этих этапах.
Постановка задачи математического моделирования объекта исследования на содержательном уровне. Как и в любой задаче, в ее постановке приводится объект исследования, его техническая функция, дается краткое описание объекта; формулируются цели задачи, описываются условия, при которых эти цели должны быть достигнуты, и указывают ограничения, которым должны удовлетворять результаты решения задачи.
Построение концептуальной модели объекта моделирования. Переход от содержательной (технической) постановки задачи к математической, т.е. переход от описания объекта в терминах предметной области к его описанию на языке математических формул и уравнений, во многих задачах связан со значительными трудностями, обусловленными сложностью самого объекта моделирования. В этих случаях, применяя методы системного анализа, разрабатывается концептуальная модель объекта моделирования. Она представляет собой совокупность гипотез и допущений, отражающих существенные с точки зрения цели моделирования свойства объекта, его поведение, взаимодействие с объектами окружающей среды.
На основании принятых гипотез и допущений устанавливается множество входных и выходных параметров, с помощью которых в дальнейшем будет строиться математическая модель объекта. Кроме того, определяются законы и закономерности, характеризующие физическую сущность протекающих в объекте явлений и процессов. При необходимости строится структурная модель объекта, отражающая состав элементов технического объекта, взаимосвязи этих элементов между собой и связи технического объекта, как системы, с окружающей средой.
Полученная концептуальная модель объекта позволяет конкретизировать содержательную постановку задачи моделирования и составляет основу для построения математической модели объекта моделирования.
Разработка математической модели объекта и проверка ее корректности. Учитывая, что математическая модель (ММ) должна отражать важнейшие свойства исследуемого объекта, стремятся создать или выбрать такую ММ, основу построения которой составляет физическая, экономическая, биологическая и т. п. сущность объекта, и является характерной для многих, относящихся к данной предметной области, объектов. Процесс разработки или выбор ММ определяется целями исследования и степенью детализации объекта моделирования, выполненной на этапе построения его концептуальной модели.
При изучении физических явлений и процессов, возникающих и протекающих в объекте, моделирование осуществляется на микроуровне, где объект представлен в виде сплошной среды, взаимодействующей с объектами окружающей среды. При этом разработка ММ осуществляется с использованием математического аппарата теории упругости и пластичности, теплофизики, гидравлики и др. Математическая модель объекта микроуровня представляет собой систему дифференциальных уравнений, с частными производными дополненную уравнениями и неравенствами, описывающими начальные и граничные условия.
Исследование процесса взаимодействия изучаемого объекта, как некоторой системы, с объектами внешней среды проводится моделированием на макроуровне. Заметим, что при разработке концептуальной модели объекта моделирования методом анализа структурного моделирования были установлены состав элементов объекта, их технические функции и математические модели этих элементов. Это позволяет методом синтеза построить полную ММ этого объекта, как единого целого. Она может представлять собой алгебраическое или дифференциальное уравнение, или систему этих уравнений, которые отражают состав элементов системы, законы их функционирования, способы объединения, характер их взаимодействия между собой и взаимодействие самого объекта с окружающей средой.
В случаях, когда математические модели разрабатываются для объектов, в которых используемые параметры являются, по своей физической природе, случайными величинами, то в зависимости от целей моделирования используются методы теории случайных процессов, теории марковских процессов, эвристического программирования, вероятностно-статистические методы. При этом в зависимости от вида объекта (простой или сложный) его математическая модель может представлять собой алгебраическое или дифференциальное уравнение, либо математическую модель на метауровне в виде системы обыкновенных дифференциальных уравнений, системы логических уравнений, системы дифференциальных уравнений Колмогорова и др.
Проверка корректности математической модели включает следующие операции:
1) контроль размерностей величин, используемых в модели и соблюдения правил теории размерности (приравниваться и складываться могут только величины одинаковой размерности);
2) контроль порядков величин (при сложении малозначимые величины могут быть исключены);
3) контроль физического смысла, т. е. проверке того, что соотношения между параметрами модели отражают физическую или иную сущность объекта моделирования;
4) контроль характера зависимостей – проверке того, что выходные параметры модели изменяются от входных параметров по соотношениям, вытекающим из математической модели, также как следует из физической сущности изучаемого объекта;
5) контроль экстремальных ситуаций, т. е. выяснению соответствия отражения соотношениями математической модели состояния реального объекта, если входные параметры модели или их комбинации приближаются к предельно допустимым для них значениям, обычно к нулю, единице или бесконечности.
6) контроль начальных и граничных условий, включающий проверку того, что эти условия сформулированы в математической модели и при ее решении выходные параметры удовлетворяют этим условиям;
7) контроль математической замкнутости, состоящий в проверке возможности получения однозначного решения математической модели.
Выбор метода решения математической модели. Выбор метода решения математической модели во многом определяется ее видом. Вместе с тем, при наличии возможности получения решения модели и аналитическим методом, и численным методом предпочитают использовать численный метод. Это объясняется тем, что, как правило, требуется получение результатов решения в числовой форме, что во многих случаях достигается с меньшими трудозатратами численными методами.
Разработка программы решения математической модели на ЭВМ. Успешное выполнение работ по разработке алгоритма и программы его реализации на ЭВМ зависит от уровня владения технологиями программирования, алгоритмическими языками, имеющегося программного обеспечения и т. д.
Проверка адекватности математической модели. Заключается в оценке степени соответствия результатов, полученным по разработанной математической модели, данным эксперимента или тестовой задачи.
Практическое использование математической модели объекта исследования. Полностью определяется целями построения моделей. Они могут использоваться для изучения свойств и особенностей поведения моделируемого объекта, как моделируемые блоки в различных САПР и АСУ (автоматизированных системах управления), при построении оптимизационных моделей и моделей-имитаторов сложных систем и комплексов.
Контрольные вопросы по теме 6
1. Поясните на конкретном примере сущность моделирования изучаемого объекта (устройства, процесса, явления).
2. Чем отличается физическое и аналоговое моделирование, как разновидности материального моделирования?
3. Какому требованию должны удовлетворять основные единицы измерения величин?
4. Что собой представляют константы подобия оригинала и модели? Как устанавливаются их значения?
5. Приведите теоремы подобия, определяющие правила переноса результатов исследования модели на оригинал.
6. С какой целью осуществляют обследование объекта моделирования?
7. Опираясь на знания изученных ранее дисциплин, приведите из них пример постановки технической задачи моделирования объекта на содержательном уровне. Постройте концептуальную модель этого объекта моделирования. Приведите его математическую модель. Произведите проверку корректности математической модели.
8. Выполните проверку размерностей величин полученной математической модели движения тела массой m, брошенного вертикально вверх от Земли массой M
,
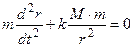в которой r – расстояние между центром Земли и центром тяжести брошенного тела; k – гравитационная постоянная, k = (6,67±0,01)·1011 Н·м2·кг-2.
9. В чем позволяет убедиться проверка адекватности ММ?
Темы научных исследований
Приведенные требования к выбираемой теме исследований позволяют всесторонне оценить и установить пригодность ее для данной научно-исследовательской организации. Однако во многих случаях при планировании тем возникает потребность в выборе наиболее перспективных, экономически обоснованных тем. В этих случаях используют количественные критерии оценки экономической эффективности темы исследований.
Предварительная оценка экономической эффективности выбранной темы научного исследования может быть выполнена с использованием критерия экономической эффективности kэ = Эп / Зи , где Эп – предполагаемый экономический эффект от внедрения; Зи – затраты на научные исследования.
Однако критерий kэ не учитывает объем внедряемой продукции, период внедрения, поэтому более объективным является критерий, вычисляемый по формуле
,
в которой: Сг – стоимость продукции за год после освоения результатов научного исследования и внедрения в производство; Т – продолжительность производственного внедрения в годах; Зо – общие затраты на выполнение научного исследования, опытное и промышленное освоение продукции и годовые затраты на ее изготовление по новой технологии.
Разработка рабочей гипотезы
Гипотеза - это научно обоснованное предположение о непосредственно наблюдаемом факте или о причине, которая вызывает данное следствие. В отличие от теории, которая представляет достоверные научные знания, гипотеза отражает предположительные научные знания в форме предположений или догадок, к которым прибегают при построении теории или при постановке эксперимента для проверки той или иной теории.
Гипотезы, как и идеи, носят вероятностный характер. На их основе осуществляются поиски новых научных результатов – в этом суть и назначение гипотезы как формы развития науки. Поэтому каждая гипотеза подвергается проверке, в процессе которой убеждаются, что она не противоречит никаким другим уже доказанным гипотезам и что следствия, вытекающие из нее, совпадают с наблюдаемыми явлениями.
Если гипотеза согласуется с наблюдаемыми фактами, то ее называют законом или теорией.
В качестве примеров можно привести высказанные в свое время гипотезы о возможности превращения тепловой и электромагнитной энергии в механическую, построенные на базе закона сохранения и превращения энергии. Эти гипотезы стали достоверными знаниями после изобретения паровых машин и электрических двигателей.
Разработка рабочей гипотезы – это центральная задача, которую решают на подготовительном этапе теоретических и экспериментальных исследований. Сущность этой задачи заключается в выдвижении научного предположения о сущности, развитии (протекании) и других признаках, свойствах изучаемого явления и объяснении выдвинутого предположения. Естественно, что и само предположение и его объяснение на момент разработки рабочей гипотезы имеют вероятностный характер и требуют своего подтверждения последующими исследованиями (теоретическими или экспериментальными или теми и другими).
Гипотеза играет весьма существенную роль в научных исследованиях, она:
· помогает осмыслить накопленный конкретный эмпирический материал исследований;
· позволяет определить факторы процесса, явления, т. е. причины, основные условия, движущие силы, которые обуславливают состояние, поведение, развитие рассматриваемого объекта;
· может дать более или менее полное предположительное объяснение результатов выполненных ранее исследований изучаемого объекта.
При разработке гипотезы придерживаются следующих требований и рекомендаций.
1. Гипотеза формулируется по отношению к определенной предметной области. Базой для гипотезы являются факты, которые могут получить объяснение на основе выдвигаемой гипотезы.
2. Гипотеза может быть сформулирована только на основании заранее выявленных факторов, предопределяющих состояние, развитие объекта, иначе говоря, она связана с независимыми переменными (факторами), влияющими на изменение зависимых переменных (параметров объекта).
3. Гипотеза формулируется так, чтобы можно было рассуждать об объекте, не обращаясь к эмпирическому материалу. Наличие новых теоретических обобщений и положений является необходимым условием плодотворной работы. Гипотеза должна способствовать логическому построению выводов в области исследований, давать возможность использования математического аппарата;
4. Гипотеза плодотворна в том случае, если она предоставляет исследователю такие же возможности, какие он получает от использования законов и теорий, уже известных науке.
5. В разрабатываемой гипотезе следует выделять наиболее важные и решающие, а также возможные причинные связи и взаимодействия, вероятное направление и ход развития явления в целом.
6. Ход развития явления, связи и взаимодействия причин его обуславливающих, желательно отображать графиками предполагаемых их функциональных зависимостей, пусть даже в безмасштабном приближенном виде.
7. При наличии возможности развитие рассматриваемого явления или процесса, взаимодействие их факторов следует представить в математической форме – формулами, уравнениями, системой уравнений и т. п. Такая предварительная аналитическая разработка способствует детализации методики последующих как теоретических, так и экспериментальных исследований.
Наряду с этими требованиями и рекомендациями следует иметь в виду, что никакое, даже достаточно полно математически разработанное гипотетическое предположение о поведении объекта исследования, никакая модель объекта не в состоянии полно отобразить реальный объект с его огромным количеством действующих второстепенных факторов. Поэтому все гипотетические предположения в большей или меньшей степени нуждаются в уточнениях, доработках, а иногда и в радикальной замене новыми гипотезами.
Вопросы самостоятельной работы по теме 7
1. Перечислите этапы научно-исследовательской работы, выполняемые в процессе решения поставленной научной проблемы (или научного вопроса). Приведите конкретные наименования этапов Вашей научно-исследовательской работы, выполняемой в рамках подготовки выпускной магистерской работы.
2. Что стремятся выявить (установить, выделить, сформулировать) на этапе литературного обзора информации по теме исследования? Какими результатами известных исследований Вы обладали на момент постановки заданной темы? Какие предварительные результаты Вы уже имеете на данный момент выполнения этого этапа исследования?
3. Какую информацию содержит технико-экономическое обоснование темы научено-исследовательской работы? Какие возможности предоставляет технико-экономическое обоснование темы исполнителю данной темы?
[1] Newtoni J. Principia matematica phylosophiae naturalis. Lib. II, Sect. VII. Propos. 32, 33, 1686.
Лекция 2
2018/2019 уч. г.
Тема 5. Теоретические исследования
Лк – 0,5 час. ПЗ – 2 час. СРС 3 час.
1. Цель и задачи теоретических исследований.
2. Основы системного подхода в теоретических исследованиях.
2.1. Принципы системного подхода.
2.2. Понятие системы. Анализ и синтез систем.
3. Математический аппарат теоретических исследований.
3.1. Математический аппарат построения математических моделей.
3.2. Методы решения математических моделей.
Дата: 2019-02-19, просмотров: 230.
