При проведении экспериментальных или теоретических исследований результаты исследования представляются числовыми значениями, полученными путем измерений тех или иных величин, характеризующих рассматриваемый объект. Измерение любой величины Q представляет собой сравнение ее с другой величиной q, имеющей ту же физическую природу. В результате определяется, во сколько раз Q > q или Q < q. Является очевидным, что величина q должна иметь определенное значение, позволяющее единообразно оценивать любые величины Qi одинаковые с q физической сущностью. Эти определенные значения q называются единицами измерения, например, метр, секунда и т. д. Набор не противоречащих друг другу единиц измерения образует систему единиц. В настоящее время используется международная система СИ, в которой основными единицами выбраны: масса (кг), длина (м), время (с), сила тока (А), температура (К), сила света (Кандела, Кд). Остальные величины, называемые вторичными, могут быть выражены через основные по формулам, которые показывают размерность вторичной величины. Например, скорость можно выразить определительным уравнением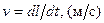 
, а размерность ее указывается при помощи взятого в квадратные скобки символа этой величины [V] = [L] [T]-1, где [L] и [T] – размерности длины и времени.
Аналогично можно найти размерности любой вторичной величины, связанной с основными единицами соответствующим определительным уравнением, в частности:
cилы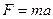 
(Н) 
;
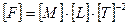работы 
(Дж)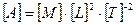 
;
мощности 
(Вт)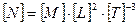 
;
электрического напряжения 
(В)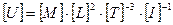 
;
электрического сопротивления 
.
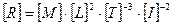Как видно из приведенных выражений, размерность любой физической величины представляет собой произведение возведенных в степень размерностей основных единиц. При решении задач механики используются только три основные единицы измерения (кг, м, с). Для таких задач размерность любой величины задачи можно записать в виде:
.
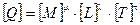что легко заметить из приведенных выше выражений.
В качестве основных (первичных) единиц измерения могут быть выбраны любые другие, но при этом должны быть выполнены следующие требования:
1. Произвольно выбранные размерности, например, [U1], [U2] и [U3] (рассматриваем для простоты только механические системы) должны являться независимыми функциями [M], [L] и [T], т. е. при любых α и β
.
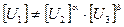2. Возможно обратное однозначное преобразование, т. е. [M], [L] и [T] можно единственным образом выразить через [U1], [U2] и [U3].
Определим условия для выполнения этих требований. Пусть размерности записаны в виде:
;
;
.
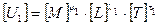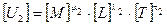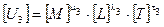После логарифмирования этих уравнений получим:
;
;)
.
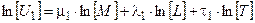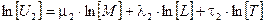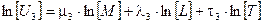Полученная система представляет собой систему линейных алгебраических уравнений относительно неизвестных [M], [L] и [T]. Из курса высшей математики известно, что такая система имеет единственное решение, если ее определитель, составленный из коэффициентов системы
,
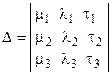будет отличен от нуля. Так как [M], [L] и [T] являются независимыми друг от друга, то 
и, следовательно, будет выполняться требование 2.
Рассмотрим два примера о возможности перехода от одних единиц измерения к другим.
Пример 1. Можно ли принять в качестве первичных единиц измерений силу, время и длину?
Обозначим U1 = F, U2 = T, U3 = L. Тогда их размерности будут:
; 
; 
.
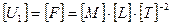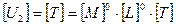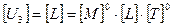Составим определитель из коэффициентов этой системы уравнений
.
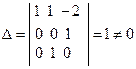Так как , то в качестве первичных единиц измерений можно принять силу, время и длину. Заметим, что в данном случае имеем так называемую техническую систему единиц.
Пример 2. Можно ли принять в качестве первичных единиц измерений силу, скорость и мощность?
Обозначим U1 = F, U2 = V, U3 = N. Тогда их размерности будут:
; 
; 
.
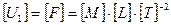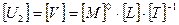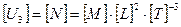Составим определитель полученной системы уравнений
.
Поскольку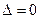 
, то требование 2 выбора первичных единиц измерений не выполняется. Следовательно, в качестве первичных единиц измерений принять силу, скорость и мощность нельзя? Заметим, к этому заключению можно прийти, рассматривая формулу мощности N = FV, в которой хорошо видна взаимозависимость единиц измерения, рассматриваемых в качестве первичных.
Выше отмечалось, что при решении задач механики используются три основные единицы измерения: масса (кг), длина (м), время (с). Вместе с тем, как показано в работе [4], число основных единиц можно изменить как в сторону увеличения их количества, так и уменьшая их число. Методические приемы таких изменений числа основных единиц можно найти [2, 4].
Основные понятия теории подобия
Выше было отмечено, что при моделировании изучаемых явлений обязательным является использование определенных соотношений, определяющих условия перехода от модели к исследуемому объекту (оригиналу). Такие соотношения устанавливаются на основе теории подобия и принципа размерности. Особая ценность теории подобия заключается в том, что она позволяет получить при моделировании объектов обоснованно обобщенные выводы и установить строгие границы их применения.
Подобие явлений характеризуется соответствием (в частном случае пропорциональностью) величин, участвующих в описании изучаемых явлений, происходящих в оригиналах и моделях. По степени соответствия параметров модели и оригинала выделяют следующие виды подобия.
Абсолютное подобие. Представляет собой абстрактное понятие, реализуемое только умозрительно, поскольку это понятие требует полное тождество состояний или явлений в пространстве и времени.
Полное подобие. Это подобие таких процессов, протекающих во времени и пространстве, которые достаточно полно для поставленных целей данного исследования определяют изучаемое явление.
Неполное подобие. Этот вид подобия используется при изучении процессов только во времени или только в пространстве. Так, электромеханические процессы в синхронном генераторе могут быть подобны во времени, без соблюдения геометрического подобия полей внутри машины (т. е. подобия в пространстве).
Приближенное подобие. Реализуется при некоторых упрощающих допущениях, приводящих к искажениям, заранее оцениваемым количественно.
Примеры моделирования при полном, неполном и приближенном моделировании приведены в работе [4].
Гениальное предвидение науки о подобии явлений было высказано Ньютоном во II – й его книге «Principia[1]» в 1686 г., который изложил принципы механического, кинематического и динамического подобий. Но только в 1848 г. член французской академии наук Жозеф Бертран впервые установил основное свойство подобных явлений, сформулировав первую теорему подобия, теорему о существовании инвариантов (критериев) подобия. Эта первая теорема подобия была сформулирована для механических явлений. Согласно этой теореме в природе существуют только те подобные явления, у которых критерии одинаковы.
Вторая теорема подобия устанавливает возможность преобразования физических уравнений, отражающих взаимосвязи между характеристиками объектов, в форму критериальных уравнений. Эта теорема была выведена русским ученым А. Федерманом в 1911 г. и несколькими годами позже, в 1914 г., американским ученым Букингэмом (Buckingham J.).
Первая и вторая теоремы устанавливают свойства подобных явлений, но не указывают, по каким признакам можно установить, что явления подобны. Ответ на этот вопрос дается третьей теоремой подобия, доказательство которой было выполнено М. В. Кирпичевым в 1930 г.
Все три теоремы являются базой современной теории подобия, отражающей общие закономерности подобия явлений и процессов.
Из геометрии известно. что подобные фигуры обладают свойством равенства соответствующих углов и равенства отношения сходственных сторон одному и тому же постоянному числу. именуемому масштабным коэффициентом (или просто масштабом) подобия n
,
где 
, 
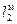и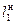 
, 
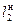- сходственные линейные размеры двух подобных фигур (условно модели – «м» и натуры – «н»).
Понятие подобия может быть распространено на любые физические явления при выполнении условия, что все величины, характеризующие рассматриваемое явление, например, плотность ρ, температура t, скорость v и др., должны быть подобными, т. е. для них должны иметь место следующие соотношения:
; 
; 
,
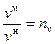где величины nρ , nt, nv – являются константами подобия.
Константы подобия для сложных физических явлений, характеризуемыми многими величинами, не могут быть выбраны произвольно, поскольку между этими величинами существуют определенные связи. Например, для сходственных частиц подобных тел скорость их движения составляет:
для первого тела (натуры)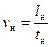 
и для второго (модели) 
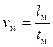, где скорость v равна отношению пути l, пройденного частицей тела за промежуток времени t, к этому промежутку времени.
Разделив почленно два написанных равенства одно на другое, получим
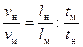. (1)
На основании определения подобия имеем следующие соотношения:
; 
; 
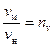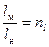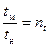. (2)
Подставляя в уравнение (1) вместо отношения величин их константы подобия, находим
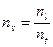или 
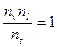. (3)
Наряду с этим из (1) после группирования величин с индексом «м» и «н» получим
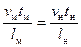. (4)
Члены последнего уравнения являются безразмерными объединениями величин, характеризующих различные стороны рассматриваемого явления. Для подобных явлений эти объединения сохраняют одно и то же числовое значение, т. е. для рассматриваемого случая можем записать
.
Такие безразмерные объединения (комплексы) величин называются критериями подобия и обозначаются через πi. Помимо выше приведенного, это могут быть
; 
; 
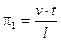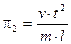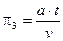и т. д.
Такие критерии получают из анализа уравнений, описывающих рассматриваемые процессы или явления (обычных алгебраических таких как, например, для скорости, мощности и т. п., а также более сложных, в т. ч. дифференциальных). Более того, критерии подобия можно составить и при отсутствии аналитической зависимости между исследуемыми величинами. В этом случае используется теория размерностей [2, 4].
Правила перехода при моделировании от модели к оригиналу при их подобии базируются на трех теоремах подобия.
Содержание первой теоремы теории подобии определяет достаточное условие подобия двух объектов (модели и оригинала), которое должно быть соблюдено при установлении связей между величинами, характеризующими различные свойства, поведение и др. стороны этих объектов.
Теорема 1. Подобные между собой объекты имеют одинаковые критерии подобия.
Согласно этой теореме, чтобы модель и оригинал были подобны, необходимо выбрать S определяющих параметров, включая в них при необходимости характеристики начальных и граничных условий. Из этих параметров можно составить (S - r) независимых критериев подобия, где r – число принятых в рассматриваемом случае основных единиц измерения. При этом для всех составленных критериев подобия πi должно соблюдаться условие:
, где i = 1, 2, 3, …, (S - r).
См., например, уравнение (4).
Теорема 2 (π-теорема). Эта теорема гласит: «чтобы данные, полученные из опыта, можно было бы непосредственно распространить на подобные явления, их необходимо представить в виде зависимостей между критериями подобия», т. е. зависимостей вида
.
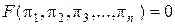Зависимости такого вида называются критериальными уравнениями.
Использование таких уравнений позволяет не только распространить результаты исследования модели на оригинал, но и значительно уменьшить количество величин, непосредственно участвующих в экспериментальном или теоретическом исследовании. Поскольку критерии подобия являются безразмерными, упрощается нахождение зависимостей между величинами, характеризующими изучаемый объект.
Теорема 3. Эта теорема определяет признаки подобия объектов. Она утверждает: «Подобны те явления, условия однозначности которых подобны, а составленные из условий однозначности критерии подобия численно равны». Вспомним, что под условиями однозначности понимают дополнительные условия, которые в совокупности с дифференциальным уравнением однозначно определяет единичное явление. К условиям однозначности в самом общем случае относятся: геометрические параметры изучаемого объекта (форма, размеры), механические и физические свойства, начальные условия, условия на граничных поверхностях объекта и др.
В частности, при исследовании процесса резания при обработке точением к условиям однозначности относятся следующие данные [5]:
1) геометрические характеристики резца (α, γ, φ, φ1, r,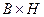 
,…), размеры среза и детали;
2) теплофизические и механические свойства обрабатываемого и инструментального материала (λ, cρ, σв, E,…);
3) граничные условия, к которым относятся принимаемые законы распределения напряжений, интенсивностей тепловых потоков и другие факторы, действующие на граничных поверхностях рассматриваемых объектов;
4) начальные условия, которые в зависимости от исследуемого процесса (теплового, механического – силового и т. п.) могут отражать распределение температуры, напряжений, перемещений и т. д. в начальный момент времени.
Пример. Поставлена задача моделирования перемещения x в моменты времени t груза массой m, который колеблется на пружине в вязкой среде, силы сопротивления которых равны: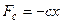 
; 
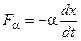, где c – жесткость пружины, Н/м; α – коэффициент вязкого трения, Н/(м/с), x - величина перемещения груза в момент времени t, (м).
Груз в момент времени t = t0, вследствие приложения ударной нагрузки, начал движение с начальной скоростью v0.
Известно, что математическая модель движения груза для заданных в задаче условий имеет вид дифференциального уравнения
с начальными условиями:
; 
.
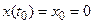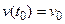Является очевидным, что перемещение x груза является функцией величин m, c, α, t, v
.
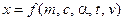Полагаем, что изучение колебательного движения груза в реальном объекте будет осуществляться на модели одинаковой с оригиналом физической природой. Следовательно, движение тела в объекте – оригинале и в его модели будут описываться соответственно уравнениями:
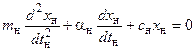; (5)
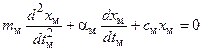, (6)
в которых индексами «н» и «м» обозначены величины, с помощью которых описано колебательное движение груза в оригинале и его материальной модели соответственно.
Для установления критериев подобия, прежде всего, введем константы подобия:
для перемещения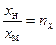 
;
для времени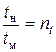 
;
для массы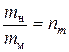 
для жесткости пружины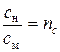 
;
для коэффициента вязкого трения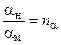 
;
для скорости 
.
Поскольку параметр x является функцией ряда величин, отражающих различные стороны исследуемого объекта (свойства отдельных элементов, время и др.), то выбор значений констант подобия не может быть произволен. Он определяется связями и отношениями, которые существуют между параметром x и этими величинами.
Размерности всех членов уравнений (5) и (6) одинаковы, знак дифференциала не влияет на размерность. Поэтому, опустив знаки дифференцирования, можем поделить все члены уравнений (5) и (6) на их первый член соответственно. В результате получим по два безразмерных комплекса величин для оригинала и модели:
; 
; 
; 
.
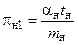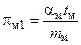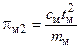Согласно первой теореме подобия, для подобных объектов полученные комплексы (критерии подобия) должны быть одинаковыми (idem), т. е.
; 
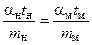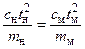. (7)
Условия (7) принято записывать в виде
; 
.
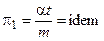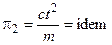Для определения условий выбора значений констант подобия подставим в равенства (7) вместо величин x, m, c, α, t их выражения через константы подобия, т. е. mн = nmmм, cн = nccм, αн = nααм, tн = nttм. Получим
; 
.
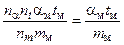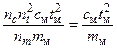Отсюда получаем условия выбора констант подобия
; 
.
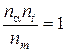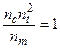Кроме того, согласно третьей теореме подобия, должно соблюдаться подобие условий однозначности. В нашем случае должно соблюдаться подобие начальных условий, т. е.
; 
.
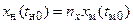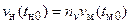Так как 
и 
, то, поделив почленно эти равенства одно на другое, получим еще один критерий подобия
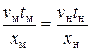, т. е. 
.
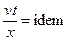Из последнего равенства находим еще одно условие выбора констант подобия
.
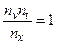Дата: 2019-02-19, просмотров: 278.
