Выше отмечалось, что линия взаимного пересечения поверхностей вращения представляет собой в общем случае сложную пространственную кривую линию, состоящую из нескольких частей. Примером тому является, в частности, линия взаимного пересечения прямого конуса вращения с цилиндром. При этом отмечалось также, что в особых случаях линии взаимного пересечения поверхностей вращения могут представлять собой и плоские кривые (рис. 178).
Это происходит в том случае, когда в каждую из пересекающихся поверхностей вращения можно вписать общую сферу. Тогда линия пересечения поверхностей представляет собой пару плоских кривых линий. При расположении плоскости симметрии фигур параллельно, например, фронтальной плоскости проекций, проекции плоских кривых пересечения представляют собой отрезки прямых, соединяющие точки пересечения главных меридианов поверхностей вращения.

Рис. 178
На чертеже (рис. 179, а) прямой усеченный конус вращения пересекается с цилиндром, ось вращения которого является профильно-проецирующей прямой. Построение профильной проекции заданных на чертеже фигур свидетельствует о том, что пересекающиеся поверхности вращения имеют две общие точки 5 и 6, в которых они касаются друг друга.
Пересекающиеся поверхности вращения, имеющие две общие точки касания, называются поверхностями двойного соприкосновения.
Установлено, что линия пересечения поверхностей двойного соприкосновения распадается на пару плоских кривых, плоскости которых проходят через прямую, соединяющую точки прикосновения.
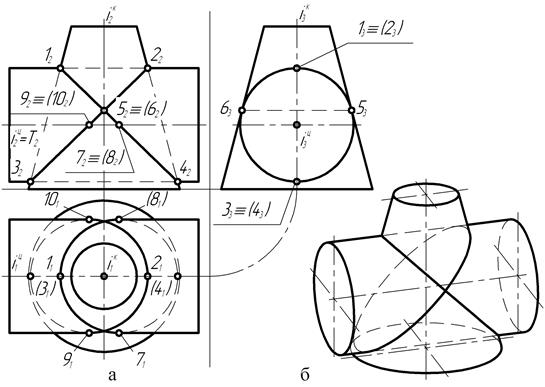
Рис. 179
Прямая 5-6 (53-63; 52-62) и является такой прямой, через которую проходят плоскости кривых взаимного пересечения поверхностей вращения. При заданном расположении фигур на чертеже фронтальные проекции плоских кривых пересечения представляют собой отрезки прямых: 12-42 и 22-32. Горизонтальные 11, 21, 31 и 41 проекции опорных точек кривых пересечения располагаются на следе главной меридиональной плоскости поверхностей вращения.
Не все проекции точек кривых пересечения будут видимыми на горизонтальной плоскости проекций. Положения фронтальных проекций точек видимости 72, 82, 92 и 102 – определяются в пересечении фронтального Т2 (тау два) следа горизонтальной секущей плоскости, проведённой через ось вращения цилиндра. Построение горизонтальных проекций опорных и произвольных точек плоских кривых пересечения производится с помощью параллелей усеченного конуса вращения. Соединив в определенной последовательности горизонтальные проекции точек, получают недостающие проекции плоских кривых пересечения.
На рис. 179, б представлено наглядное изображение взаимного пересечения поверхностей вращения двойного соприкосновения.
На рис. 180 показаны различные примеры расположения фронтальных проекций взаимного пересечения поверхностей двойного соприкосновения, используемых, например, при конструировании различного рода трубопроводов из листового материала.

Рис. 180
Сравнительная простота в построении проекций линии взаимного пересечения поверхностей вращения, имеющих двойное соприкосновение, предопределяет необходимость проведения предварительного анализа взаимного расположения проекций заданных на чертеже фигур с целью выявления наличия у них двойного соприкосновения.
Вопросы для самопроверки
1. Что представляет собой в общем случае линия взаимного пересечения поверхностей вращения?
2. В каком случае линия взаимного пересечения поверхностей вращения может представлять собой две плоские кривые линии?
3. Какие поверхности вращения называются поверхностями двойного соприкосновения?
4. Каким образом можно установить принадлежность пересекающихся поверхностей вращения к поверхностям двойного соприкосновения?
5. Что представляют собой линии пересечения поверхностей вращения двойного соприкосновения и через какую прямую они должны проходить?
6. Какие точки кривой пересечения поверхностей вращения называются опорными?
7. Какие точки кривой пересечения поверхностей вращения называются произвольными?
8. Назовите способы построения проекций произвольных точек кривой пересечения поверхностей вращения.
9. В каком случае применяется способ вспомогательных секущих плоскостей?
10. Изложите последовательность выполнения графических построений в случае применения способа вспомогательных секущих плоскостей.
11. Каким условием определяется выбор вида и расположения вспомогательной секущей плоскости?
12. Чем объясняется сокращение трудоёмкости графических построений проекций кривых пересечения двух поверхностей вращения, одна из которых является цилиндрической?
13. В каком случае применяется способ вспомогательных секущих сфер? Перечислите условия, ограничивающие применение этого способа.
14. Какие поверхности вращения называются соосными?
15. Какой вид имеет линия пересечения соосных поверхностей вращения? Чем определяется количество линий пересечения соосных поверхностей вращения?
16. В каком случае сфера является соосной с поверхностью вращения?
17. В чем состоит сущность способа вспомогательных секущих сфер?
18. Какие существуют разновидности способа секущих сфер?
19. Какие сферы называются концентрическими?
20. Какие сферы называются эксцентрическими?
21. На чем основано применение способа концентрических секущих сфер?
22. Какие существуют ограничения в применении способа концентрических секущих сфер?
23. Каким образом определяются значениями минимального и максимального радиусов концентрических секущих сфер?
24. На чем основано применение способа эксцентрических секущих сфер?
25. Какие существуют ограничения в применении способа эксцентрических секущих сфер?
26. На основании какого свойства поверхностей вращения определяются положения центров эксцентрических секущих сфер?
3.5. Последовательность выполнения построений графического решения задачи 8 [ 1 ]
Задача – построить линию пересечения конуса вращения с
цилиндром вращения.
Графическое решение задачи выполняют на листе чертежной бумаги (ватмане) формата А3 (297´420 мм), расположив длинную сторону формата горизонтально. Карандашом тонкими линиями вычерчивают рамки формата, чертежа и в правом нижнем углу длинной стороны формата рамку основной надписи. Левую половину поля чертежа (рис. 181, а) используют для построения исходного чертежа задачи. С этой целью на расстоянии 130 мм от верхней рамки поля чертежа проводят горизонтальную прямую линию и на ней на расстоянии 150 мм от левой рамки поля чертежа отмечают положение точки 0 – начала отсчета координат. Через точку 0 проводят вертикальную прямую линию, перпендикулярную горизонтальной прямой. Вводят обозначения осей проекций X, Y и Z. Из табл. 7 методических указаний [1] выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности конуса вращения и цилиндра вращения.
Определяют положение на чертеже проекций центра (точка К) окружности радиуса R основания конуса вращения. На фронтальной плоскости проекций отмечают положение проекции вершины конуса. С помощью циркуля и линейки тонкими линиями вычерчивают фронтальную и горизонтальную проекции прямого конуса вращения. Ось вращения конуса представляет собой горизонтально-проецирующую прямую. Фронтальную проекцию оси вращения конуса выполняют штрихпунктирной линией.
Затем строят проекции оси вращения цилиндра. Осью вращения цилиндра является фронтально-проецирующая прямая точки Е. Основаниями цилиндра являются окружности радиуса R1. Образующие цилиндра имеют длину, равную 3R1, и делятся пополам фронтальной меридиональной плоскостью конуса вращения. Окружности основания и образующие цилиндра выполняют сплошными тонкими линиями. Не следует наносить координатные размеры на исходный чертеж задачи.
Графическому решению задачи должен предшествовать анализ расположения заданных геометрических фигур относительно друг друга и плоскостей проекций.
По условию задачи оси поверхностей вращения – взаимно перпендикулярные скрещивающиеся проецирующие прямые. Ось вращения цилиндра является фронтально-проецирующей прямой. Поэтому цилиндрическая поверхность является проецирующей по отношению к фронтальной плоскости проекций.
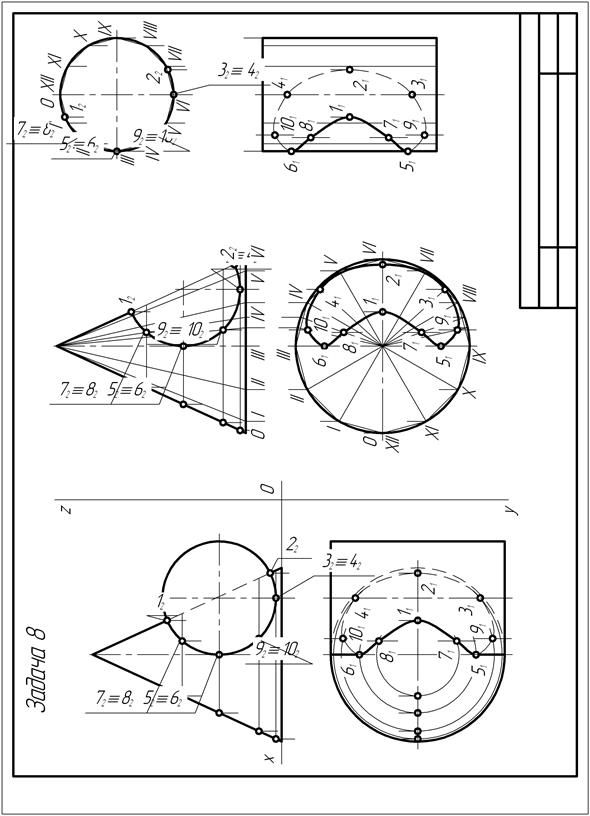
| Рис. 181 |
Расположение на чертеже фронтальной проекции цилиндра внутри контура проекции конуса вращения свидетельствует о том, что заданные поверхности пересекаются друг с другом. Линия их взаимного пересечения представляет собой сложную пространственную кривую, точки которой принадлежат обеим поверхностям. Причем точки кривой взаимного пересечения фигур располагаются только на их наружных поверхностях. И так как цилиндрическая поверхность является фронтально-проецирующей, становится вполне очевидным тот факт, что с фронтальной проекцией цилиндра – окружностью, расположенной внутри контура треугольника – проекции главного меридиана прямого конуса вращения, совпадает фронтальная проекция кривой взаимного пересечения заданных поверхностей.
Для построения горизонтальной проекции кривой пересечения конуса с цилиндром на её фронтальной проекции выделяют положения проекций опорных и нескольких произвольных точек.
На фронтальной плоскости проекций отмечают, прежде всего, положения точек 12 и 22 пересечения фронтальной проекции цилиндра с главным меридианом конуса. Эти точки относятся к числу опорных. Из них: точка 12 является фронтальной проекций самой высокой, а точка 22 – самой правой точек кривой пересечения фигур. Точки 32 и 42 являются проекциями самых низших точек кривой пересечения. Точки 52 и 62 являются проекциями точек видимости горизонтальной проекции кривой пересечения. Точки 72, 82, 92 и 102 являются проекциями произвольных точек кривой. Их положение на чертеже выбирается произвольно.
Дальнейшее графическое решение задачи сводится к построению горизонтальных проекций отмеченных точек кривой пересечения заданных геометрических фигур.
Так как цилиндрическая поверхность является фронтально-проецирующей, то построение горизонтальных проекций точек кривой пересечения возможно лишь на основании принадлежности их боковой поверхности конуса. Поэтому построение горизонтальных проекций отмеченных точек кривой выполняют с помощью параллелей прямого конуса вращения.
Для этого на фронтальной плоскости проекций внутри контура треугольника – главного меридиана прямого конуса вращения, через соответствующие фронтальные проекции точек кривой проводят прямые, перпендикулярные фронтальной проекции оси вращения конуса. Отмечают точки пересечения этих прямых с одной из сторон главного меридиана конуса.
Через эти точки проводят линии связи до пересечения с горизонтальным следом главной меридиональной плоскости конуса. Раствором циркуля, равным расстоянию от этих точек до горизонтальной проекции оси вращения конуса, проводят окружности – горизонтальные проекции параллелей соответствующих точек кривой пересечения. И, наконец, через фронтальную проекцию выбранной точки кривой пересечения проводят линию связи и отмечают точки пересечения её с горизонтальной проекцией точек кривой взаимного пересечения поверхностей.
Соединив с помощью лекала плавной кривой горизонтальные проекции точек, получат горизонтальную проекцию кривой пересечения прямого конуса с цилиндром вращения. При этом видимые проекции точек кривой пересечения соединяют сплошной толстой линией, а невидимые – штриховой линией. После построения горизонтальной проекции кривой взаимного пересечения поверхностей вращения производят окончательную обводку линий чертежа карандашом. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.
Все цифровые и буквенные обозначения следует выполнить чертежным шрифтом.
3.6. Последовательность выполнения построений графического решения задачи 9 [ 1 ]
Задача – построить развертки пересекающихся цилиндра вращения и конуса вращения; показать на развертках линии их пересечения.
Построение разверток пересекающихся поверхностей вращения производят в следующей последовательности:
- в заданный конус вписывают 12-гранную пирамиду, в цилиндр 12-гранную призму;
- строят развертки 12-гранной пирамиды и призмы;
- наносят на развертки точки кривой взаимного пересечения поверхностей и соединяют их с помощью лекала плавными линиями.
Для этого в правой части поля чертежа решения задачи 8 (рис. 181, б, в) вычерчивают проекции каждой из заданных поверхностей с кривой пересечения. В прямой конус вращения вписывают 12-гранную пирамиду, а в цилиндр вращения – 12-гранную призму. Отмечают на чертежах положение ребер оснований и боковых поверхностей многогранников. При этом некоторые из ранее рассмотренных точек кривой пересечения оказываются расположенными непосредственно на ребрах боковых поверхностей многогранников. Через другие точки кривой проводят прямые в соответствующих гранях многогранников.
Для построения развертки конуса вращения определяют натуральные величины ребер основания и боковой поверхности пирамиды, а также натуральные величины расстояний от точек кривой пересечения до вершины пирамиды – конуса вращения.
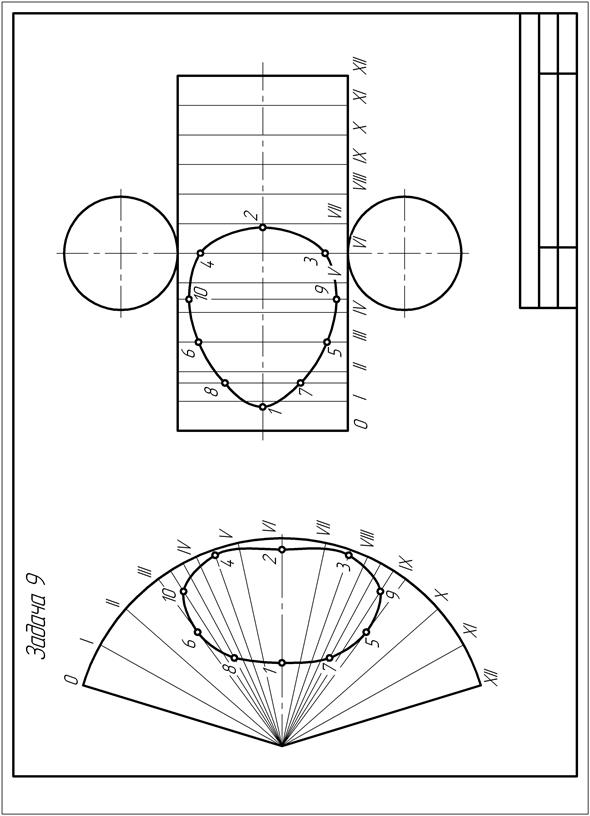
| Рис. 182 |
Основание вписанной 12-гранной пирамиды спроецировалось на горизонтальную плоскость проекций в натуральную величину. Для определения натуральной величины расстояния от точек кривой пересечения до вершины пирамиды используют способ вращения вокруг горизонтально-проецирующей прямой, совпадающей с осью вращения конуса. Ребра и прямые боковой поверхности пирамиды, на которых расположены точки кривой пересечения, поворачивают в положение, параллельное фронтальной плоскости проекций. Графически это преобразование выполняют следующим образом: на фронтальной плоскости проекций через фронтальные проекции точек кривой пересечения проводят прямые линии параллельно оси проекций Х до пересечения с главным меридианом конуса. Расстояние проекции точки на главном меридиане до вершины конуса соответствует натуральной величине расстояния точки кривой пересечения до вершины пирамиды.
В левой части поля чертежа (рис. 182, а) произвольно выбирают положение вершины конуса – пирамиды и раствором циркуля, равным натуральной величине образующей конуса, проводят дугу окружности. На ней откладывают 12 равных отрезков, соответствующих натуральной величине ребра основания пирамиды. Соединив их с центром дуги окружности – вершиной пирамиды, конуса, получают развёртку боковой поверхности 12-гранной пирамиды. На ребрах или прямых боковой поверхности пирамиды откладывают натуральные величины расстояний соответствующих точек кривой пересечения до вершины пирамиды, взятые на фронтальной плоскости проекций, на стороне главного меридиана конуса.
Соединив с помощью лекала в определенной последовательности точки плавной линией, получают на развертке боковой поверхности прямого конуса вращения линию его пересечения с цилиндром вращения.
Последовательность построения развёртки цилиндра вращения
(рис. 182, б) аналогична построениям графического решения задачи 4.
При этом натуральные величины ребер основания призмы, а также натуральные величины расстояний точек кривой пересечения от соответствующего ребра боковой поверхности призмы (рис. 182, в), измеряют на фронтальной плоскости проекций. Натуральные величины расстояний точек кривой пересечения от какого-либо основания призмы измеряют на горизонтальной плоскости проекций.
Соединив в определенной последовательности лекальной линией точки, получают на развертке боковой поверхности кривую пересечения цилиндра вращения с прямым конусом вращения.
После построения на развертках кривых пересечения производят окончательную обводку карандашом линий чертежа. Сплошные тонкие линии вспомогательных построений необходимо сохранить.
Все буквенные и цифровые обозначения следует выполнять чертежным шрифтом.
3.7. Последовательность выполнения построений графического решения задачи 10 [ 1 ]
Задача – построить линию пересечения фронтально-проецирующего цилиндра вращения с поверхностью открытого тора.
Графическое решение задачи выполняют на листе чертежной бумаги (ватмане) формата А3 (297×420 мм), расположив длинную сторону формата горизонтально. Карандашом тонкими линиями вычерчивают рамки формата, чертежа и в правом нижнем углу формата рамку оснований надписи.
Левую половину поля чертежа используют для построения исходного чертежа задачи. На расстояние 180 мм от верхней рамки поля чертежа проводят горизонтальную прямую линию и на ней на расстоянии 145 мм от левой рамки чертежа отмечают положение точки 0 – начало отсчета координат. Через точку 0 проводят вертикальную прямую линию, перпендикулярную горизонтальной прямой. Вводят обозначения осей проекций X, Y и Z. Из табл. 8 методических указаний [1] выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности тора и цилиндра вращения.
Ось вращения тора располагается на чертеже перпендикулярно фронтальной плоскости проекций. Ее фронтальная проекция совпадает с положением точки 0, а горизонтальная проекция – с положением оси проекций Y. Числовое значение радиуса производящей окружности R1 выбирается из табл. 8 в зависимости от номера варианта задачи. Точка К – центр производящей окружности. Поверхность тора ограничена двумя основаниями, одно из которых располагается в горизонтальной плоскости проекций, другое – в профильной.
Осью вращения цилиндра радиусом r является фронтально-проецирующая прямая, проходящая через точку Е. Образующие цилиндра имеют длину, равную 3r, и делятся пополам фронтальной меридиональной плоскостью тора. Исходный чертеж задачи (рис. 183) выполняют сплошными тонкими линиями. Оси вращения, симметрии – штрих-пунктирными линиями.
Графическому решению задачи предшествует анализ расположения заданных геометрических фигур относительно друг друга и плоскостей проекций.
Известно, что линия взаимного пересечения поверхностей вращения представляет собой сложную пространственную кривую, точки которой
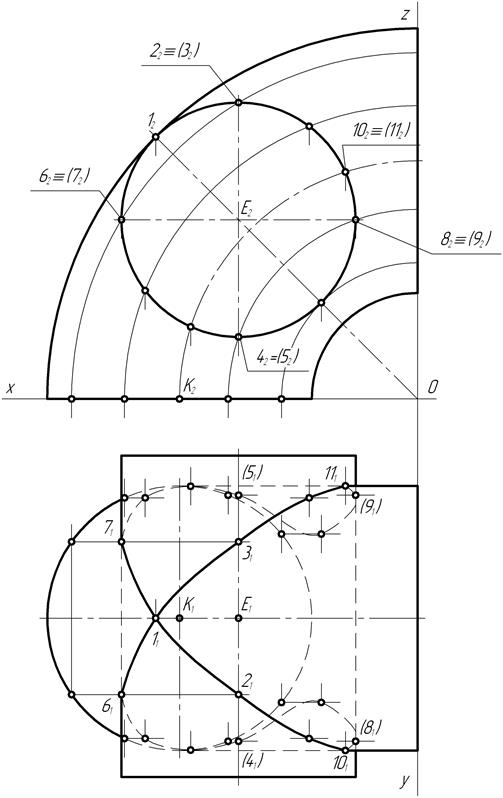
Рис. 183
принадлежат обеим фигурам и располагаются только на их наружных поверхностях. По условию задачи цилиндрическая поверхность является фронтально-проецирующей. Поэтому вырожденная фронтальная проекция цилиндра – окружность, является фронтальной проекцией искомой линии взаимного пересечения заданных поверхностей вращения.
Для построения горизонтальной проекции кривой пересечения цилиндра вращения с тором на её фронтальной проекции выделяют положения опорных точек и нескольких произвольных точек.
На фронтальной плоскости проекций отмечают прежде всего положение точки касания поверхностей, если это происходит в результате построения исходного чертежа задачи. Для этого через центры окружностей проводят прямую, которая и выявляет положение на чертеже точки I2. Проекция I2 точки касания располагается на главном меридиане тора, а её горизонтальная I1 проекция – на горизонтальном следе главной меридиональной плоскости. Необходимо отметить, что главная меридиональная плоскость делит поверхности и линию их взаимного пересечения на две симметричные части. В связи с этим часть проекций точек кривой пересечения на фронтальной плоскости проекций будут видимыми, другие – невидимыми. Эти точки являются конкурирующими. Невидимые проекции точек заключают в круглые скобки.
На чертеже выделяют положения точек 22, 32 и 42, 52. Эти точки относятся к числу экстремальных точек кривой пересечения. Точки 22 и 32 – самые высокие, а точки 42 и 52 – самые низкие. Точки 62, 72 и 102, 112 являются точками видимости. Они делят горизонтальную проекцию кривой пересечения на видимую и невидимую части. Остальные точки относятся к числу произвольных. Их фронтальные проекции на чертеже выделяются таким образом, чтобы они располагались на дугах окружностей, проведённых из точки 0.
Построение горизонтальных проекций точек кривой пересечения производится на основании принадлежности их наружной поверхности тора. Каждая из точек поверхности тора совершает вращательное движение вокруг оси его вращения. Траектория вращения представляет собой окружность – параллель. Так как ось вращения тора перпендикулярна фронтальной плоскости проекций, параллель – окружность проецируется на фронтальную плоскость проекций без искажения в натуральную величину, а на горизонтальную плоскость проекций – в прямую линию, параллельную оси проекций X. Каждая из точек поверхности тора вращается вокруг оси по окружности определённого радиуса. Поэтому проекции точки поверхности должны располагаться на соответствующих проекциях этой окружности – параллели. Это свойство и положено в основу графических построений горизонтальных проекций точек кривой пересечения по имеющимся на чертеже их фронтальным проекциям. При этом следует помнить о том, что главная меридиональная плоскость тора делит его поверхность на две симметричные части. В связи с этим горизонтальные проекции точек кривой пересечения располагаются на чертеже симметрично относительно горизонтального следа главной меридиональной плоскости тора.
Соединив плавной лекальной кривой горизонтальные проекции точек в порядке расположения их на фронтальной проекции кривой – окружности цилиндра, получают горизонтальную проекцию кривой взаимного пересечения тора с цилиндром вращения. При этом видимые горизонтальные проекции точек соединяют сплошной толстой линией, невидимые – штриховой линией.
После построения горизонтальной проекции кривой взаимного пересечения поверхностей вращения производят окончательную обводку карандашом линий чертежа. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.
Все цифровые и буквенные обозначения следует выполнять чертёжным шрифтом.
3.8. Последовательность выполнения построений графического решения задачи 11 [ 1 ]
Задача – построить линию пересечения фронтально-проецирующего цилиндра вращения с поверхностью наклонного конуса с круговым основанием.
Графическое решение задачи выполняют на листе чертежной бумаги (ватмане) формата АЗ (297´420 мм), расположив длинную сторону формата горизонтально. Карандашом тонкими линиями вычерчивают рамки формата, чертежа и в правом нижнем углу формата рамку основной надписи. Проводят координатные оси X, Y и Z таким образом, чтобы последующие построения проекций заданных геометрических фигур равномерно располагались бы на поле чертежа. Отмечают положение точки О – начало отсчета координат. Из табл. 9 методических указаний 1 выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности цилиндра вращения и наклонного конуса.
Определяют положения на чертеже проекций К2, К1 центра К окружности R основания и вершины S2 (S2, SI) конуса. На фронтальной и горизонтальной плоскостях проекций тонкими штрихпунктирными линиями соединяют одноименные проекции вершины и центра окружности основания конуса. Затем на фронтальной плоскости проекций соединяют проекцию S2 вершины конуса с крайними точками проекции окружности основания. Получают фронтальную проекцию конуса. На горизонтальной
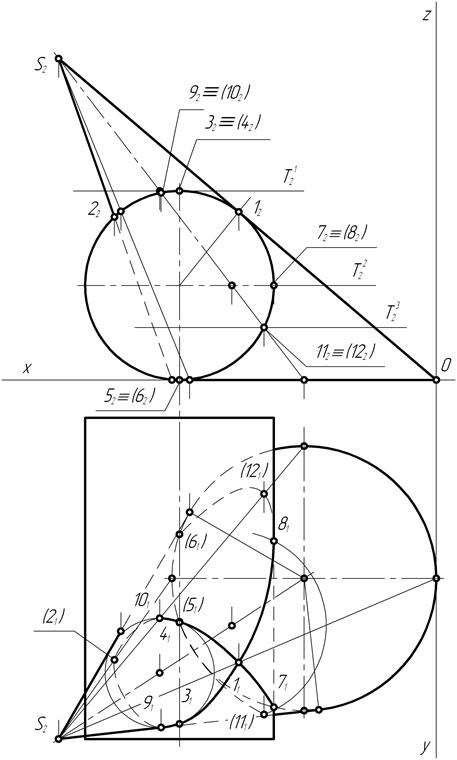
Рис. 184
плоскости проекций вначале вычерчивают тонкой сплошной линией окружность основания конуса, а затем через точку S1 проводят прямые, касательные к этой окружности. Получают горизонтальную проекцию наклонного конуса.
Построение проекций фронтально-проецирующего цилиндра не вызывает затруднений. На исходный чертеж задачи не следует наносить координатные размеры заданных геометрических фигур.
В связи с тем, что по условию задачи поверхность цилиндра вращения является проецирующей, на чертеже задачи (рис. 184) уже имеется одна (фронтальная) проекция линии взаимного пересечения поверхностей. Ее фронтальная проекция располагается на окружности – вырожденной проекции цилиндра, находящейся внутри контура фронтальной проекции наклонного конуса.
Известно, что линия взаимного пересечения поверхностей вращения представляет собой сложную пространственную кривую, точки которой принадлежат обеим фигурам. Построение горизонтальных проекций точек кривой взаимного пересечения заданных геометрических фигур возможно лишь на основании признака принадлежности их поверхности наклонного конуса с круговым основанием.
Это предопределяет использование в качестве вспомогательных секущих плоскостей горизонтальных плоскостей уровня. Именно такие секущие плоскости пересекают поверхность наклонного конуса по окружностям – геометрически простым линиям, параллельным основанию. Окружность сечения на горизонтальную плоскость проекций проецируется без искажения в натуральную величину.
Фронтальная проекция этой окружности сечения представляет собой прямую линию, параллельную оси проекций X и расположенную внутри контура фронтальной проекции наклонного конуса. Натуральная величина диаметра окружности сечения ограничивается точками пересечения горизонтальной секущей плоскости с фронтальной проекцией контура наклонного конуса. Центр окружности сечения располагается на фронтальной проекции оси вращения конуса. Соответственно горизонтальная проекция центра окружности сечения располагается на горизонтальной проекции оси вращения конуса. Проекция точки, через которую проведена вспомогательная горизонтальная секущая плоскость, располагается на соответствующих проекциях окружности сечения.
На фронтальной проекции кривой пересечения отмечают положения опорных и нескольких произвольных точек. Вначале отмечают положения точек взаимного пересечения контуров фронтальных проекций заданных геометрических фигур – точки 12, 22 и 72, 82. Затем отмечают положения экстремальных точек: 32, 42 – самых высоких; 72, 82 – самых правых. Точки 7 и 8 являются одновременно и точками видимости горизонтальной проекции кривой пересечения. Остальные точки, например, 92, 102 и 112, 122, относятся к числу произвольных точек кривой.
Построение горизонтальных проекций точек кривой пересечения производят в следующей последовательности:
- на фронтальной плоскости проекций через выбранную проекцию точки кривой пересечения проводят вспомогательную горизонтальную секущую плоскость, например, Т1 (тау), Т2 и т. д.;
- отмечают точку пересечения её с фронтальной проекцией оси вращения конуса. Эта точка является фронтальной проекцией центра окружности сечения;
- при помощи линии связи определяют положение горизонтальной проекции центра окружности сечения на горизонтальной проекции оси вращения конуса;
- строят горизонтальную проекцию окружности сечения и при помощи линии связи определяют положение горизонтальной проекции точки кривой, через фронтальную проекцию которой была проведена вспомогательная горизонтальная секущая плоскость.
Подобным образом получают на чертеже необходимое количество горизонтальных проекций точек кривой пересечения поверхностей.
Соединив плавной лекальной кривой горизонтальные проекции точек в порядке расположения их на фронтальной проекции кривой – окружности цилиндра, получают горизонтальную проекцию кривой пересечения фронтально-проецирующего цилиндра вращения с поверхностью наклонного конуса с круговым основанием. Видимые горизонтальные проекции точек соединяют сплошной толстой линией, невидимые – тонкой штриховой линией.
После построения горизонтальной проекции кривой взаимного пересечения поверхностей вращения производят окончательную обводку карандашом линии чертежа. Толстыми сплошными линиями обводят наружный контур проекций фигур. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.
Все цифровые и буквенные обозначения следует выполнять чертёжным шрифтом.
3.9. Последовательность выполнения построений графического решения задачи 12 [ 1 ]
Задача – построить линию пересечения закрытого тора с
поверхностью наклонного цилиндра вращения.
Построение исходного чертежа выполняют в правой половине поля чертежа задачи 10, расположив оси проекции так, чтобы свободное поле
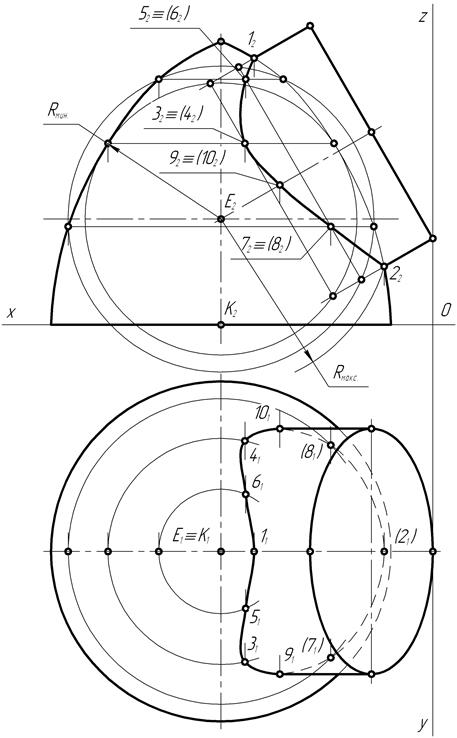
Рис. 185
чертежа было рационально использовано фронтальными и горизонтальными проекциями заданных поверхностей.
Из табл. 10 методических указаний 1 выбирают, согласно номеру варианта задачи, величины, которыми задаются поверхности вращения.
Вначале строят фронтальную К2 и горизонтальную К1 проекции точки К центра окружности R основания тора. Эта окружность представляет собой экваториальную параллель тора, располагающуюся непосредственно в горизонтальной плоскости проекций. Поэтому её фронтальная проекция представляет собой прямую линию, совпадающую с осью проекций X. Строят фронтальную и горизонтальную проекции этой параллели и проводят на чертеже фронтальную проекцию оси вращения тора. Затем строят на фронтальной плоскости проекций главный меридиан тора, представляющий собой замкнутую линию, состоящую из двух пересекающихся на оси вращения дуг окружностей радиуса 2R и отрезка прямой – проекции экваториальной параллели.
На фронтальной плоскости проекций определяют положение фронтальной Е2 проекции точки Е пересечения вертикальной оси тора с наклонной осью цилиндра вращения радиуса r = 2R/3. Ось цилиндра вращения пересекается с осью поверхности тора в точке Е под углом σо, различным для каждого из вариантов задачи. Основание цилиндра вращения касается профильной плоскости проекций. С учётом этих особенностей расположения пересекающихся поверхностей вращения строят их фронтальные и горизонтальные проекции (рис. 185). Построение проекций кривой пересечения производят по точкам, принадлежащим обеим поверхностям вращения.
Представленные на чертеже поверхности вращения имеют общую фронтальную плоскость симметрии, совпадающую с положением их главной меридиональной плоскости. Это обстоятельство позволяет определить на чертеже положения двух опорных точек кривой пересечения.
На фронтальной плоскости проекций в пересечении главных меридианов выявляются положения двух проекций 11 и 21 точек, принадлежащих каждой из поверхности вращения. Их горизонтальные 11 и 21 проекции располагаются на следе главной меридиональной плоскости. Одна из них является высшей, а другая – низшей экстремальными точками кривой пересечения.
Так как ни одна из заданных поверхностей не является проецирующей, положение других точек пересечения кривой определяют с помощью либо вспомогательных секущих плоскостей, либо вспомогательных секущих сфер. Способ вспомогательных секущих плоскостей использовать в данном случае не представляется возможным, так как нельзя обе поверхности пересечь одной плоскостью и получить в сечении геометрически простые линии – окружности или прямые. Так как заданные поверхности имеют общую фронтальную плоскость симметрии и оси вращения пересекаются, применяется способ вспомогательных секущих концентрических сфер.
Точка E2 пересечения фронтальных проекций осей вращения является центром секущих сфер. Максимальный радиус секущей сферы равен наибольшему расстоянию центра сфер до точек пересечения главных меридианов поверхностей вращения. Минимальный радиус секущей сферы равен наибольшему радиусу окружности, вписанной в одну из поверхностей вращения.
Из точки Е2 пересечения фронтальных проекций осей вращения поверхностей проводят последовательно ряд сфер радиусом, меньшим максимального, но большим минимального. Каждая из сфер пересекает обе поверхности вращения по окружностям. Их фронтальные проекции представляют собой отрезки прямых, соединяющие точки пересечения окружности секущей сферы с главными меридианами поверхностей. В пересечении этих отрезков прямых и находятся фронтальные проекции точек, например, 32…82, принадлежащих обеим поверхностям.
Подобным образом определяют на чертеже положения фронтальных проекций некоторого количества промежуточных (случайных) точек кривой пересечения.
Горизонтальные проекции точек кривой пересечения поверхностей строят при помощи параллелей закрытого тора.
Соединив плавной лекальной кривой одноимённые проекции точек с учётом их видимости на чертеже, получают фронтальную и горизонтальную проекции линии пересечения закрытого тора с поверхностью наклонного цилиндра вращения.
В пересечении фронтальных проекций кривой и оси вращения цилиндра определяют положения точек 92 и 102 видимости горизонтальной проекции кривой пересечения.
Видимые проекции точек кривой пересечения соединяют сплошной толстой линией, невидимые – штриховой линией.
Производят окончательную обводку карандашом линий чертежа. Тонкие сплошные линии вспомогательных построений, линии связи на чертеже задачи следует сохранить.
Все цифровые и буквенные обозначения следует выполнять чертежным шрифтом.
Литература
Основная
1. Гордон В.О. Курс начертательной геометрии: учеб. пособие для студентов вузов / В.О. Гордон, М.А. Семенцов-Огиевский; под ред. В.О. Гордона, Ю.Б. Иванова. 25-е изд., стереотип. – М.: Высшая школа, 2003. – 272 с.
2. Гордон В.О. Сборник задач по курсу начертательной геометрии: учеб. пособие / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. Ю.Б. Иванова. – 9-е изд., стереотип. – М.: Высшая школа, 2003. –
320 с.
3. Инженерная графика: в 3 кн. Кн. 1. Начертательная геометрия. Геометрическое проекционное черчение: учебник / П.Н. Учаев, В.И. Якунин, С.Г. Емельянов и др. – М.: Высшая школа, 2007. – 687 с.
4. Иванов Г.С. Начертательная геометрия: учебник для вузов / Г.С. Иванов. – М.: Машиностроение, 1995. – 224 с.
5. Нартова Л.Г. Начертательная геометрия: учеб. пособие для студентов техн. спец. вузов / Л.Г. Нартова, В.И. Якунин. – М.: Издат. центр «Академия», 2005. – 288 с.
Дополнительная
6. Локтев О.В. Краткий курс начертательной геометрии: учебник / О.В. Локтев. – М.: Высшая школа, 2006. – 136 с.
7. Локтев О.В. Задачник по начертательной геометрии: учеб. пособие / О.В. Локтев, П.А. Числов. – М.: Высшая школа, 2004. – 104 с.
8. Григорьев В.Г. Инженерная графика: учебник для вузов / В.Г. Григорьев, В.И. Горячев, Т.П. Кузнецова. – М.: Мир Автокниг, 2007. – 464 с.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ …………………………………………………………………..3
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ПРЯМОЙ И ПЛОСКОСТИ……………………………………………………………….4
1.1. Положение прямой в пространстве и её комплексные чертежи………………………………………………………...………...4
1.1.1. Общие сведения………………………………...…………………4
1.1.2. Построение проекций прямой общего положения……………..5
1.1.3. Построение проекций прямых уровня………………………......8
1.1.4. Построение проекций проецирующих прямых………………..12
Вопросы для самопроверки……………………………………………..16
1.2. Положение плоскости в пространстве и её комплексные чертежи…...……………………………………………………............17
1.2.1. Способы задания плоскости на чертеже…………………...….17
1.2.2. Проецирующие плоскости……………………...…..………..…19
1.2.3. Плоскости уровня………………………………………….……23
1.2.4. Плоскости общего положения………...………………………..26
Вопросы для самопроверки……………………………………….…….27
1.3. Взаимное положение прямой и плоскости……………….……28
1.3.1. Принадлежность прямой и точки плоскости……………….….28
1.3.2. Прямая наибольшего наклона плоскости…….………………..29
1.3.2.1. Определение натуральной величины угла наибольшего
наклона плоскости к плоскостям проекций…………………..30
1.3.3. Параллельность прямой плоскости…………….……………....31
1.3.4. Пересечение прямой с плоскостью…………………………….32
1.3.4.1. Пересечение прямой общего положения с
проецирующей плоскостью……………………………………32
1.3.4.2. Пересечение проецирующей прямой с плоскостью
общего положения………………………………...…………….33
1.3.4.3. Пересечение прямой общего положения с плоскостью
общего положения……………………………..………………..34
1.3.5. Определение видимости проекций прямой и плоскости…….35
1.3.6. Перпендикулярность прямой плоскости………………………36
Вопросы для самопроверки…………………………………………..…39
1.4. Последовательность выполнения построений графического
решения задачи 1/1/………...……………………….……….….40
1.4.1. Построение исходного чертежа задачи…………………….…..40
1.4.2. Построение проекций линии пересечения треугольников…...40
1.4.3. Определение видимости проекций треугольников………...….46
1.4.4. Определение натуральной величины треугольника ABC…….49
1.5. Многогранные поверхности………………………………….…56
1.5.1. Образование многогранных поверхностей и построение их комплексных чертежей…………………………………….……56
1.5.2. Определение видимости проекций ребер многогранника……59
1.5.3. Принадлежность точки и прямой многогранной
поверхности……………………………………………………...61
1.5.4. Пересечение многогранника с прямой и плоскостью.
Общие положения……………………………………………….62
1.5.4.1. Пересечение многогранника с проецирующей плоскостью….63
1.5.4.2. Пересечение многогранника с прямой. Общие положения......64
1.5.4.3. Пересечение многогранника с проецирующей прямой………65
1.5.4.4. Пересечение многогранника с прямой общего положения…..67
1.5.4.5. Пересечение многогранника с плоскостью общего положения….68
Вопросы для самопроверки………………………………………………75
1.6. Взаимное пересечение многогранных поверхностей.
Общие положения……………………………………………….76
1.6.1. Взаимное пересечение пирамидальных и призматических поверхностей………………………………………………………77
Вопросы для самопроверки………………………………………………84
1.7. Последовательность выполнения построения графического
решения задачи 3 /1/…………………………….………………85
1.7.1. Построение исходного чертежа задачи………………………..85
1.7.2. Построение проекций линии пересечения многогранников…90
1.8. Построение разверток многогранных поверхностей.
Общие положения………………………………………………96
1.8.1. Построение разверток пирамидальных поверхностей……….96
1.8.2. Построение развертки призматической поверхности
способом нормального сечения………………………………105
1.8.3. Построение развертки призматической поверхности
способом раскатки…………………………………………….110
1.9. Последовательность выполнения построений графического
решения задачи 4 /1/…………………………………………...114
2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
ВРАЩЕНИЯ С ПРЯМОЙ И ПЛОСКОСТЬЮ…………………………121
2.1. Способы образования и задания на чертеже поверхностей
вращения……………………………………………………….121
2.2. Принадлежность точки поверхности вращения……………..133
Вопросы для самопроверки…………..…………………………………142
2.3. Пересечение поверхностей вращения с плоскостью.
Общие положения……………….…………………………….144
2.4. Пересечение поверхностей вращения с плоскостями
частного положения……………………………………………151
Вопросы для самопроверки……..……………………………………..172
2.5. Пересечение поверхностей вращения с прямой.
Общие положения……………………………………………...174
2.5.1. Пересечение поверхностей вращения с проецирующей прямой………………………………………………………………176
2.5.2. Пересечение поверхностей вращения с прямой уровня……..178
Вопросы для самопроверки………………………..…………………..187
2.6. Последовательность выполнения построений графического
решения задачи 6 /1/………………………………..………….188
3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИКА ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ ВЗАИМНОГО ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ…………………..………………………………………….192
3.1. Взаимное пересечение поверхностей вращения.
Общие положения…………………………………………..…192
3.2. Построение проекций линии взаимного пересечения
поверхностей вращения способом вспомогательных
секущих плоскостей…………………………………………...193
3.3. Построение проекций линии взаимного пересечения
поверхностей вращения способом вспомогательных
секущих сфер. Общие положения…………………………....202
3.3.1. Построение проекций линии взаимного пересечения поверхностей вращения способом концентрических
секущих сфер…………………………………………………..203
3.3.2. Построение проекций линии взаимного пересечения поверхностей вращения способом эксцентрических
секущих сфер…………………………………………………..210
3.4. Особые (частные) случаи взаимного пересечения
поверхностей вращения.............................................................216
3.4.1. Пересечение поверхностей вращения с проецирующей поверхностью вращения………………………………….…………...216
3.4.2. Взаимное пересечение поверхностей вращения двойного соприкосновения…………………………………………………219
Вопросы для самопроверки…………………………………………....221
3.5. Последовательность выполнения построений графического
решения задачи 8 /1/………………………………………..….223
3.6. Последовательность выполнения построений графического
решения задачи 9 /1/………………………………………...…226
3.7. Последовательность выполнения построений графического
решения задачи 10 /1/……………………………………….…229
3.8. Последовательность выполнения построений графического
решения задачи 11 /1/……………………………………….…232
3.9. Последовательность выполнения построений графического
решения задачи 12 /1/…………………………………….……235
ЛИТЕРАТУРА…………………..…………………………………………...239
Учебное издание
ЗАЙЦЕВ Юрий Александрович
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.
РЕШЕНИЕ ЗАДАЧИ
Учебное пособие
Компьютерная верстка Н.В. Полянская, А.Г. Землянка
Редактор О.А. Панина
Подписано в печать Формат 60х84 1/16
Бум. офсет. Усл. печ. л. Уч.-изд. л.
Тираж - экз. Заказ С.
Саратовский государственный технический университет.
410054 г. Саратов, ул. Политехническая, 77.
Отпечатано в РИЦ СГТУ. 410054 г. Саратов, ул. Политехническая, 77.
Дата: 2019-02-25, просмотров: 797.