Общие положения

Аналогично тому, как при пересечении многогранника с плоскостью (рис. 125) в сечении получается плоская геометрическая фигура, так и линия пересечения поверхности вращения с плоскостью представляет собой в общем случае плоскую геометрическую фигуру, но теперь уже кривую линию. Ее можно рассматривать как геометрическое место точек пересечения таких линий поверхности вращения, как прямолинейные образующие, меридианы или параллели с секущей плоскостью.

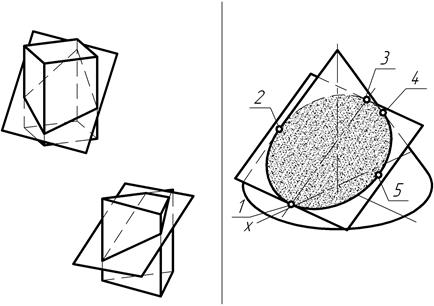
Рис. 125

Для построения на чертеже проекций кривой пересечения вначале находят положения отдельных ее точек и затем, соединяя одноименные проекции точек плавными кривыми (обычно по лекалу), получают проекции искомой линии.

Среди точек кривой пересечения, например, прямого конуса вращения с плоскостью общего положения, представленных на рис. 125, имеются такие точки, которые либо выделяются своим особым расположением по отношению к плоскостям проекции и наблюдателю, либо занимают особые места на поверхности вращения. Такие точки кривой пересечения называют опорными. К ним относятся так называемые экстремальные точки и точки видимости. Экстремальными точками являются такие точки линии пересечения, о которых обычно говорят, что они – самые, самые. Самая высшая (например, точка 3) и самая низшая (точка 1), а также самая дальняя (например, точка 2) и самая ближняя (точка 5), самая левая и самая правая точки по отношению к наблюдателю, расположенному лицом к фронтальной плоскости проекций. Точки видимости (например, точки 2 и 4) разграничивают проекции линии пересечения на видимую и невидимую части по отношению к той или иной плоскости проекций. Остальные точки кривой пересечения называются произвольными.

Если все произвольные точки кривой пересечения могут быть найдены одним общим приемом, рассмотренным ниже, то для нахождения положения опорных точек приходится для каждой из них искать свой особый прием построения, зависящий не только от вида самой поверхности вращения, но и от расположения поверхности и секущей плоскости друг относительно друга и плоскостей проекций.

Рассмотрим некоторые особенности построения опорных и произвольных точек кривой сечения на примере пересечения прямого конуса вращения с плоскостью общего положения (рис. 126, а).

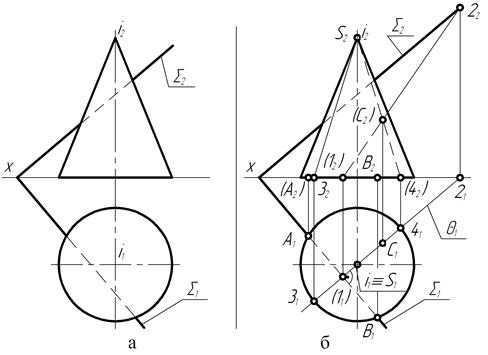
Рис. 126

На чертеже секущая плоскость å (сигма) задана следами: фронтальным – å₂ и горизонтальным – å₁. Это – один из способов задания плоскости на чертежах. Вспомним, что следом плоскости называется прямая линия, которая получается при пересечении заданной плоскости с какой-либо плоскостью проекций. И так как на чертеже оба следа плоскости располагаются под некоторым углом к оси проекции Х, то плоскость представляет собой плоскость общего положения. А поэтому кривая пересечения спроецируется на обе плоскости проекции: фронтальную и горизонтальную – в искаженном виде.

Анализ взаимного расположения заданных фигур и их расположения относительно плоскостей проекций позволяет установить на чертеже положения проекций самых низших точек кривой пересечения (рис. 126, б).

Обратите внимание на то, что фронтальная проекция основания конуса располагается непосредственно на оси проекции Х. Это значит, что основание конуса – окружность – не только лежит в горизонтальной плоскости проекции, но и пересекается со следом Σ₁ секущей плоскости в точках А₁ и В₁. Фронтальные А₂ и В₂ проекции точек располагаются на оси проекций Х. На этом основании можно сделать вывод о том, что точки
А (А₁, А₂) и В (В₁, В₂) являются самыми низшими точками кривой пересечения.

Вместе с тем, рассматривая расположение горизонтальных проекций точек А и В на чертеже, устанавливаем, что точка В является, кроме того, самой близкой к наблюдателю точкой, располагающейся на видимой части поверхности конуса. Поэтому ее фронтальная проекция будет видимой, а проекция точки А₂ – невидимой. Таким образом, одна и та же точка кривой пересечения в некоторых случаях может быть, с одной стороны, самой низшей, а с другой – самой близкой.

Естественно предположить, что если кривая пересечения имеет самые низшие точки, то должна же быть и самая высокая точка. Как определит ее положение на чертеже? Опять-таки на основании анализа расположения на чертеже проекций заданных геометрических фигур.

Секущая плоскость Σ (сигма) является плоскостью общего положения. Она определенным образом наклонена к горизонтальной плоскости проекций и по отношению к наблюдателю является восходящей. Поэтому самая высшая точка кривой пересечения фигур, как принадлежащая секущей плоскости, должна находиться, с одной стороны, на линии наибольшего наклона плоскости Σ к горизонтальной плоскости проекции. А эта линия заданной секущей плоскости располагается перпендикулярно горизонтальному Σ₁ ее следу. С другой стороны, самая высшая точка кривой пересечения принадлежит и конической поверхности, и поэтому должна располагаться на одном из меридианов. А что такое меридиан? Это есть сечение поверхности вращения плоскостью, проходящей через ось вращения.

При заданном на чертеже расположении оси вращения конуса эта плоскость является горизонтально-проецирующей. Значит, след меридиональной плоскости, в которой находится самая высшая точка кривой пересечения фигур, должен расположиться на чертеже обязательно перпендикулярно горизонтальному Σ₁ следу секущей плоскости.

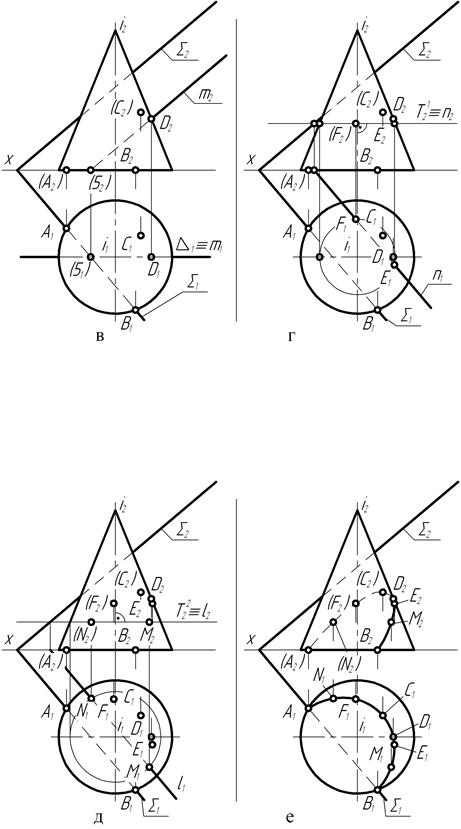
Рис. 126

Для определения конкретного положения на чертеже проекций точки видимости кривой пересечения воспользуемся вспомогательной секущей плоскостью, которая по сути дела является как бы продолжением главной меридиональной плоскости конуса. На чертеже эта вспомогательная секущая плоскость обозначена своим горизонтальным λ₁ (лямбда – 1) следом.

В пересечении вспомогательной фронтальной плоскости λ с плоскостью Σ образуется фронтальная прямая m с проекциями m₁ и m₂. Линия пересечения плоскости λ (лямбда) с конусом есть не что иное, как его главный меридиан, фронтальной проекцией которого является треугольник, с одной из сторон которого в точке Д₂ пересекается прямая m₂. Горизонтальная Д₁ проекция располагается на следе λ₁.

Точка Д (Д₁, Д₂) принадлежит секущей плоскости Σ и прямому конусу вращения. И так как проекция точки Д располагается на соответствующих проекциях главного меридиана поверхности вращения, она является следующей искомой точкой кривой пересечения, а именно – точкой видимости.

Таким образом, посредством выполнения определенных приемов, обусловленных изображением геометрических фигур на чертеже, удалось выявить положения проекций основных опорных точек кривой пересечения.

Для определения положения на чертеже проекций произвольных точек кривой пересечения используют известный способ вспомогательных секущих плоскостей.

Сущность его, применительно к рассматриваемому примеру – пересечению конической поверхности с плоскостью общего положения, состоит в том, что заданная плоскость и поверхность вращения пересекаются одной вспомогательной секущей плоскостью, чаще всего проецирующей или плоскостью уровня. Однако в некоторых случаях в качестве секущей плоскости может быть использована и плоскость общего положения.

Выбор вида и положения на чертеже вспомогательной секущей плоскости определяется условием: в пересечении поверхностей вращения с этой плоскостью должны получаться простые геометрические линии – прямые или окружности. Это условие относится непосредственно только к поверхностям вращения, так как плоскости пересекаются друг с другом в любом случае по прямой. Важно при этом, чтобы окружности сечения – параллели – проецировались бы на одну из плоскостей проекций в натуральную величину.

Для рассматриваемого примера (рис. 126, г) указанным выше условиям отвечает горизонтальная секущая плоскость, заданная на чертеже своим фронтальным T₂¹ (тау) следом, расположенным параллельно оси проекции Х.

Именно в сечении прямого конуса вращения этой плоскостью образуется плоская геометрическая линия – окружность, представляющая собой параллель конической поверхности, так как ось вращения конуса перпендикулярна горизонтальной плоскости проекций.

Можно было бы использовать в качестве вспомогательной секущей плоскости либо горизонтально-проецирующую плоскость, проходящую через ось вращения конуса, то есть конкурирующую с меридиональной плоскостью конической поверхности, либо плоскость общего положения, проходящую через вершину конуса. В сечении конуса каждой из указанных плоскостей также образуются простые геометрические фигуры – треугольники. Однако применение таких вспомогательных секущих плоскостей несколько увеличивает трудоемкость выполнения графических построений.

При пересечении вспомогательной секущей плоскости Т (τ - тау) с плоскостью Σ (сигма) образуется прямая частного положения, а именно – горизонтальная прямая. Это обстоятельство также имеет весьма существенное значение для уменьшения трудоемкости графических построений, так как проекции прямых уровня в плоскостях общего положения, заданных на чертеже следами, очень легко строить – горизонтальная проекция горизонтальной прямой плоскости Σ, например, должна располагаться параллельно ее горизонтальному Σ₁ следу.

На фронтальной плоскости проекций между точкой С₂ – самой высшей точкой и точками А₂ и В₂ – самыми низшими проекциями точек кривой пересечения проводят след – Τ₂¹ первой вспомогательной горизонтальной секущей плоскости. И строят горизонтальные проекции линий сечения фигур плоскостью Т (тау), представляющие собой: окружность – горизонтальную проекцию параллели конической поверхности и прямую n₁ – проекцию горизонтальной прямой n плоскости.

Рассматривают их взаимное расположение и устанавливают, что горизонтальная проекция параллели конуса – окружность и прямая n₁ пересекаются в точках Е₁ и F₁. Фронтальные проекции этих точек: Е₂ и F₂  находят на следе Τ₂¹  секущей плоскости.

На основании того, что проекции точек F (F₁, F₂) и Е (Е₁, Е₂) располагаются на соответствующих проекциях прямой n (n₁, n₂), принадлежащей плоскости Σ, и проекциях параллели конуса, делают вывод о том, что точки E и F принадлежат одновременно плоскости Σ, и поверхности конуса вращения. А это значит, что точки E и F принадлежат кривой пересечения прямого конуса вращения с плоскостью общего положения.

Подобным образом (рис. 126, д) определяют положения на чертеже ещё двух произвольных точек N (N₁, N₂ ) и М (М₁, М₂) кривой пересечения с помощью всё той же вспомогательной горизонтальной секущей плоскости Т (тау), но теперь уже проведённой несколько ниже фронтальных проекций точек F₂ и Е₂.

С помощью способа вспомогательной секущей плоскости можно определить положения на чертеже проекций некоторого множества произвольных точек кривой пересечения. Соединив затем плавной кривой линией по лекалу одноимённые проекции точек с учётом видимости их на чертеже, получают (рис. 126, е) фронтальную и горизонтальную проекции кривой пересечения прямого конуса вращения с плоскостью Σ общего положения.

На рис. 127 представлено наглядное изображение – прямоугольная изометрия заданных на чертеже фигур: прямого конуса вращения и секущей плоскости общего положения, а также кривая линия, полученная в результате их взаимного пересечения. На кривой обозначены положения её опорных и произвольных точек.

Таким образом, рассмотренный пример построения на чертеже проекций кривой пересечения поверхности вращения с плоскостью общего положения свидетельствует о значительной трудоемкости выполненных при этом графических построений.

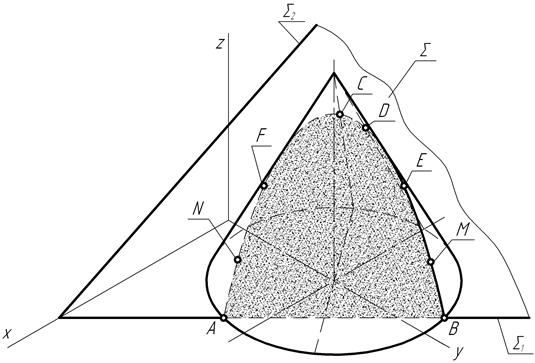
Рис. 127

Вместе с тем трудоёмкость решения подобной задачи удаётся значительно сократить преобразованием секущей плоскости общего положения в проецирующую или плоскость уровня. Это объясняется тем, что в случае использования в качестве секущей плоскости проецирующей или плоскости уровня, на чертеже всегда имеется одна из проекций кривой пересечения этой плоскости с поверхностью вращения. Тогда использование способа вспомогательных секущих плоскостей для определения положения проекций произвольных точек кривой пересечения вовсе отпадает, так как построение второй проекции кривой пересечения по сути дела сводится лишь к построению недостающих проекций её точек. Выполнение же этих построений на основании эпюрного признака принадлежности точки поверхности вращения не вызывает особых затруднений. Значительно упрощается при этом и решение такой сложной задачи, как определение положения на чертеже опорных точек кривой пересечения: экстремальных и точек видимости.

Рассмотрим конкретные примеры построения проекций линий пересечения поверхностей вращения с секущими плоскостями частного положения: проецирующими или плоскостями уровня.