Общие положения

Аналогично тому, как в случае пересечения прямой с многогранной поверхностью образуются точки, принадлежащие обеим фигурам: прямой и многограннику, так и при пересечении поверхностей вращения с прямой (рис. 140) образуются точки, принадлежащие и прямой, и поверхности вращения.

В связи с этим для построения проекций точек пересечения прямой с поверхностью вращения представляется возможным использовать в общем случае способ вспомогательной секущей плоскости. Тогда графические построения проекций точек пересечения прямой с поверхностью вращения осуществляются в следующей последовательности:

- прямую заключают во вспомогательную секущую плоскость;

- строят проекции линии пересечения вспомогательной секущей плоскости с поверхностью вращения;

- рассматривают взаимное расположение проекций прямой и линии пересечения поверхности вращения вспомогательной секущей плоскостью;

- точки взаимного пересечения одноимённых проекций прямой и фигуры сечения представляют собой проекции искомых точек пересечения поверхности вращения с прямой;

- на основании эпюрного признака принадлежности точки прямой или поверхности вращения строят вторые проекции искомых точек.

В качестве вспомогательной секущей плоскости используются чаще всего плоскости частного положения – проецирующие или плоскости уровня. Однако в некоторых случаях успешно применяются и плоскости общего положения.

Выбор вида и положения вспомогательной секущей плоскости определяется условием – поверхность вращения должна пересекаться плоскостью по графически простым линиям: прямым или окружности.

Если при пересечении многогранника плоскостью (рис. 141) в любом случае в сечении образуются графически простые фигуры – многоугольники, то сечение поверхности вращения плоскостью представляет собой графически простые фигуры – треугольники, параллелограммы, окружности, лишь при некоторых особых положениях секущей плоскости.

Так, в сечении прямого цилиндра вращения образуются графически простые фигуры – прямоугольник или окружность, только в случае пересечения его плоскостью, параллельной или перпендикулярной оси вращения.

В сечении прямого конуса вращения (рис. 142) образуются графически простые фигуры – треугольник или окружность, только в случае пере-

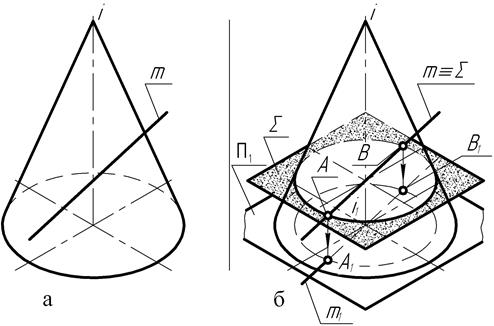
Рис. 140

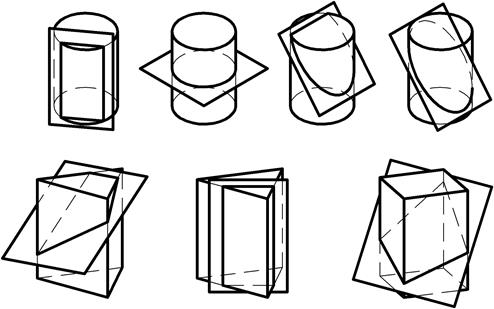
Рис. 140

сечения его плоскостью, проходящей через вершину или расположенной перпендикулярно оси вращения.

В тех случаях, когда в сечении поверхности вращения плоскостью невозможно получить графически простые фигуры сечения, приходится строить проекции кривой пересечения – эллипса, параболы, гиперболы и других, а затем определять положения точек пересечения проекций прямой с кривой линией сечения.

В некоторых случаях применение способов преобразования проекционных чертежей, в частности, способа замены плоскостей проекций, позволяют вообще отказаться от использования способа вспомогательной секущей плоскости для определения положения на чертеже проекций точек пересечения прямой с поверхностью вращения.

Рассмотрим особенности построения проекций точек пересечения поверхности вращения с прямой, занимающей в пространстве различные положения, на конкретных примерах.