Вполне очевидно, что к числу проецирующих поверхностей вращения (рис. 176) может быть отнесена лишь цилиндрическая, ось вращения которой перпендикулярна какой – либо плоскости проекций.

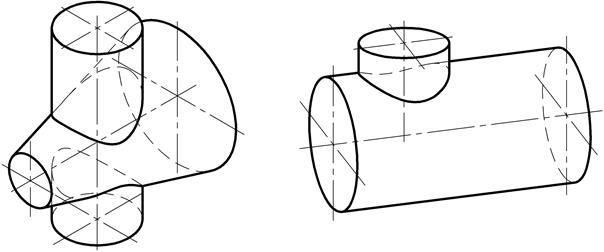
Рис. 176

Только в этом случае проекция цилиндрической поверхности вращения на одной из плоскостей проекций представляет собой окружность. Это обстоятельство весьма существенно снижает трудоёмкость построения проекций линии взаимного пересечения поверхностей вращения в связи с тем, что в этом случае одна из проекций цилиндра вращения представляет собой окружность, и именно на ней располагаются проекции точек кривой пересечения. Положение недостающих проекций точек кривой пересечения определяются на основании принадлежности их другой поверхности вращения, пересекающейся с цилиндрической.

На чертеже (рис. 177, а) прямой конус вращения пересекается с цилиндрической поверхностью, ось вращения которой является профильно-проецирующей прямой.

Анализ расположения проекций фигур на чертеже позволяет сделать вывод о том, что пересекающиеся поверхности вращения имеют две плоскости симметрии. Одна из них параллельна фронтальной плоскости проекций, проходит через ось вращения цилиндра и совпадает с главной меридиональной плоскостью поверхностей вращения.

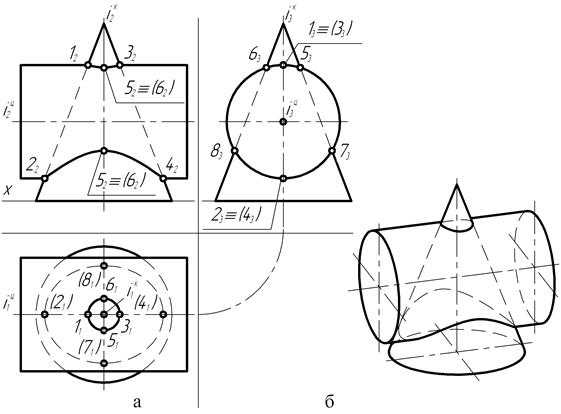
Рис. 177

Фронтальные проекции фигур представляют собой главные меридианы поверхностей вращения, и точки их пересечения: 1₂, 2₂, 3₂ и 4₂ – являются опорными точками линии их взаимного пересечения, так как принадлежат обеим поверхностям. Горизонтальные проекции 1₁, 2₁, 3₁ и 4₁ точек располагаются на следе главной меридиональной плоскости.

Точки 1 и 3 являются высшими, а точки 2 и 4 – низшими точками линии пересечения.

Построение третьей, профильной проекции фигур позволяет,
во-первых, выявить положения на чертеже профильных проекций точек линии пересечения, конкурирующей с профильной проекцией цилиндрической поверхности – окружностью, и, во-вторых, установить, что при заданном расположении фигур на чертеже имеет место случай полного проницания, а поэтому линия их взаимного пересечения представляет собой две пространственные кривые: верхнюю и нижнюю.

Профильные проекции поверхностей: треугольник и окружность, – представляют собой, по сути дела, проекции фигур сечения прямого конуса вращения и цилиндра другой плоскостью симметрии, проходящей через ось вращения конуса и параллельной профильной плоскости проекций.

В пересечении профильных проекций фигур сечения образуются точки: 5₃, 6₃, 7₃ и 8₃. Они ограничивают контур профильных проекций верхней и нижней кривых пересечения, расположенных на боковой профильно-проецирующей поверхности цилиндра. Причём точки 5₃  и 6₃ являются низшими точками верхней кривой пересечения, а точки 7₃ и 8₃ – высшими точками нижней кривой пересечения.

Остальные профильные проекции точек кривых пересечения, расположенные на окружности – проекции боковой поверхности цилиндра между точками 5₃ и 6₃, а также между точками 7₃ и 8₃, относятся к числу произвольных.

Построение фронтальных и горизонтальных проекций опорных и произвольных точек кривых пересечения выполняется с помощью параллелей прямого конуса вращения. При этом необходимо отметить, что, во-первых, проекции точек кривых пересечения должны располагаться симметрично ранее выявленным плоскостям симметрии, и, во-вторых, горизонтальные проекции точек нижней кривой пересечения являются невидимыми.

Соединив в определенной последовательности плавными линиями одноименные проекции точек, получают фронтальные и горизонтальные проекции кривых взаимного пересечения заданных на чертеже поверхностей вращения.

На рис. 177, б представлено наглядное изображение заданных на чертеже пересекающихся поверхностей вращения.

Таким образом, в случае пересечения двух поверхностей вращения, одна из которых является цилиндрической, вовсе отпадает необходимость применения каких бы то ни было особых способов построения проекций произвольных точек кривых пересечения.

В том случае, когда цилиндрическая поверхность не является проецирующей, необходимо выполнить предварительное преобразование чертежа, например, с помощью способа замены плоскостей проекций.