На чертеже (рис. 145, а) сферическая поверхность пересекается с фронтальной прямой f. В этом случае для определения положения на чертеже проекций точек пересечения необходимо воспользоваться способом вспомогательной секущей плоскости.
По расположению проекций f1 и f2 на чертеже следует, что прямую можно заключить либо во вспомогательную фронтально-проецирующую плоскость, либо во вспомогательную фронтальную плоскость, плоскость уровня. В обоих случаях кривая пересечения сферы плоскостью представляет собой окружность. Но фронтально-проецирующая плоскость наклонена к горизонтальной плоскости проекций, поэтому кривая пересечения – окружность спроецируется на горизонтальную плоскость проекций в искажённом виде и будет представлять собой эллипс. Построение же эллипса сопряжено со значительной трудоемкостью определения положений проекций его опорных и произвольных точек.
В случае использования в качестве вспомогательной фронтальной секущей плоскости, кривая пересечения – окружность спроецируется на фронтальную плоскость без искажения – в натуральную величину.
Диаметр окружности сечения равен отрезку горизонтального Λ1 следа секущей плоскости, находящегося внутри проекций экватора сферы.
Построив фронтальную проекцию окружности сечения, отмечают на чертеже точки пересечения её с фронтальной f1 проекцией прямой.
Горизонтальные проекции точек пересечения должны располагаться на горизонтальном Λ1 следе вспомогательной секущей плоскости.
Точки А (А1, А2) и В (В2, В1) являются искомыми точками пересечения сферы с фронтальной прямой f, так как положения проекций этих точек на
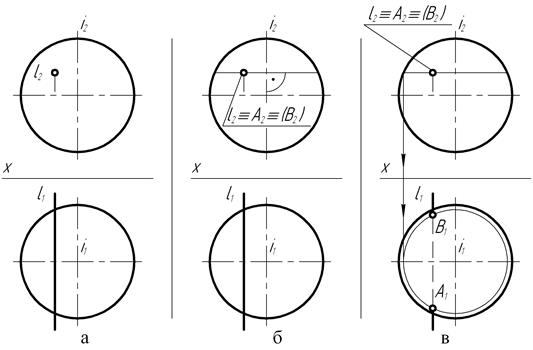
Рис. 144
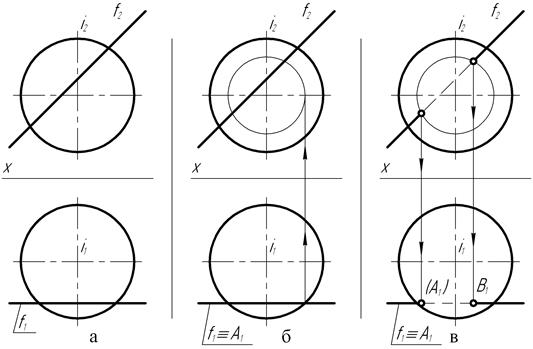
Рис. 145
чертеже полностью удовлетворяют эпюрным признакам принадлежности их обеим фигурам – сфере и прямой.
На чертеже (рис. 146, а) прямой конус вращения пересекается с горизонтальной прямой h. Если прямую заключить во вспомогательную горизонтальную плоскость q (тэта), то сечение ею прямого конуса вращения будет представлять собой окружность- параллель (рис. 146, б).
Пересечение горизонтальной проекции параллели с проекцией h1 прямой выявит положение на чертеже (рис. 146, в) горизонтальных А1 и В1 проекций точек пересечения прямой h с конусом.
Фронтальные А2 и В2 проекции точек пересечения располагаются на фронтальном θ2 следе вспомогательной секущей плоскости.
Точки А (А1, А2) и В (В2,В1) являются искомыми точками пересечения прямого конуса вращения с горизонтальной прямой h, так как положения проекций точек на чертеже полностью отвечают эпюрным признакам принадлежности обеим фигурам: прямому конусу вращения и прямой h.
На чертеже (рис. 147, а) прямой конус вращения пересекается с фронтальной прямой f. Использование в качестве вспомогательных секущих плоскостей частного положения: фронтально-проецирующей или плоскости уровня, не приносит желаемого результата (рис. 147, б). В сечении образуются графически сложные линии – эллипс или гипербола.
Аналогичный случай получения в сечении графически сложных линий имеет место и при использовании в качестве вспомогательных секущих плоскостей частного положения для построения проекций точек пересечения прямой общего положения (рис. 148, а) с поверхностью прямого конуса вращения.
Вместе с тем известно, что в случае пересечения конуса вращения с плоскостью, проходящей через его вершину, образуется графически простая фигура сечения – треугольник.
Рассмотрим особенности построения проекций точек пересечения прямой общего положения с поверхностью прямого конуса вращения в случае использования в качестве секущей плоскости общего положения, проходящей через его вершину.
Для этого (рис. 148, б) на прямой m выделяют положения фронтальных и горизонтальных проекций двух произвольных её точек, например, точки А (А2, А1) и В (В2, В1). Затем (рис. 148, в) на фронтальной плоскости проекций вершину конуса – точку S2 соединяют прямыми с точками А2 и В2 и продолжают их до пересечения с осью проекций X в точках 12 и 22.
Далее строят горизонтальные проекции прямых S1A1 и S1B1 (рис. 148, г) и на продолжениях этих прямых с помощью линий связи определяют положения горизонтальных проекций точек 11 и 21.
Соединив затем (рис. 148, д) на горизонтальной плоскости проекций точки 12 и 22 прямой, получают на чертеже проекции треугольника S12
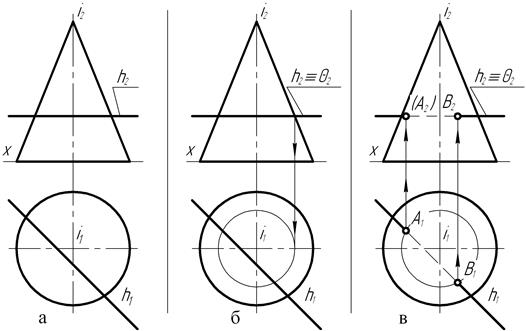
Рис. 146
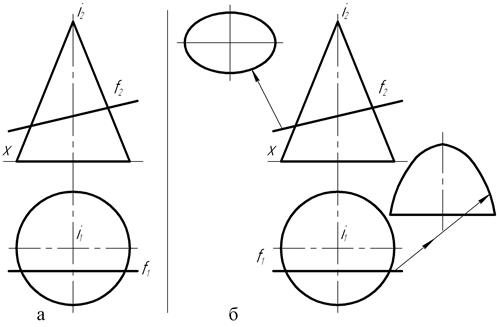
Рис. 147
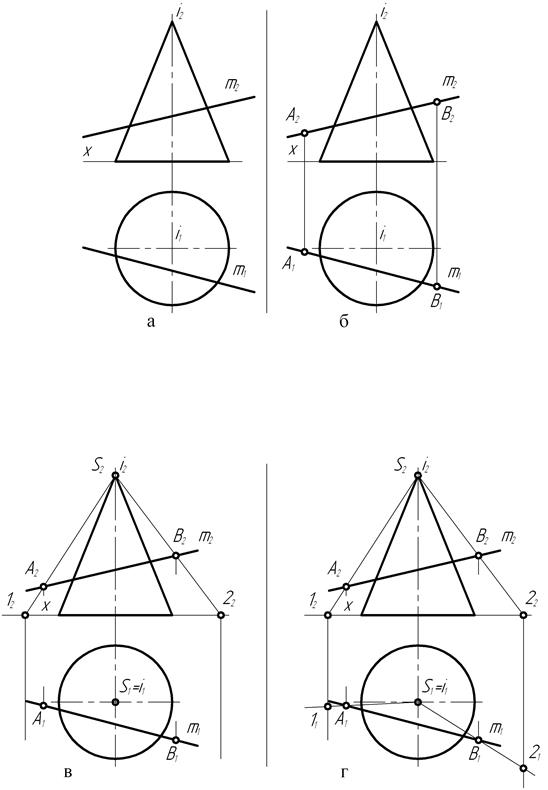
Рис. 148
(S21222 , S11121), представляющего собой плоскость общего положения. Прямая m оказалось заключённой, таким образом, во вспомогательную плоскость общего положения, проходящую через вершину S конуса. Причём прямая 11-21 представляет собой горизонтальный след секущей плоскости, который в точках 31 и 41 пересекается с проекцией основания конуса, расположенного непосредственно в горизонтальной плоскости проекций.
Соединив теперь точки 31 и 41 прямыми с точкой S1, получают треугольник S13141, представляющий собой горизонтальную проекцию фигуры сечения прямого конуса вращения плоскостью, проходящей через его вершину.
На основании принадлежности прямой m вспомогательной секущей плоскости рассматривают взаимное расположение прямой m1 и треугольника S13141. Выявляют точки С1 и Д1 их взаимного пересечения. С помощью линий связи определяют положения фронтальных С2, Д2 проекций точек, принадлежащих m.
Точки С и Д, определённые на чертеже положениями горизонтальных С1, Д1 и фронтальных С2, Д2 проекций, являются искомыми точками пересечения прямого конуса вращения с прямой общего положения.
Этот вывод сделан на том основании, что положения проекций точек С и Д на чертеже соответствуют эпюрным признакам принадлежности их обеим фигурам – прямому конусу вращения и прямой общего положения.
На чертеже (рис. 149, а) прямая l общего положения пересекается с поверхностью прямого цилиндра вращения. Точки пересечения должны располагаться на наружной цилиндрической поверхности, которая в свою очередь является проецирующей по отношению к горизонтальной плоскости проекций. Поэтому (рис. 149, б) в пересечении горизонтальных проекций прямой и цилиндра определяются положения горизонтальных 11 и 21 проекций точек пересечения прямой l с цилиндром.
Положения фронтальных 12 и 22 проекций точек пересечения (рис. 149, в) определены с помощью линий связи на проекции l2 прямой общего положения.
Таким образом, расположение на чертеже проекций точек пересечения прямой общего положения с прямым цилиндром вращения установлено только лишь на основании эпюрных признаков принадлежности точек пересечения поверхности цилиндра и прямой.
На чертеже (рис. 150, а) сферическая поверхность пересекается с прямой n общего положения. Заключение прямой n в горизонтально- или фронтально-проецирующую плоскость неизбежно приведёт к необходимости построения искажённой проекции окружности сечения, представляющей собой эллипс. Однако прямую общего положения можно преобразовать (рис. 150, б) способом замены плоскостей проекций в прямую уровня.
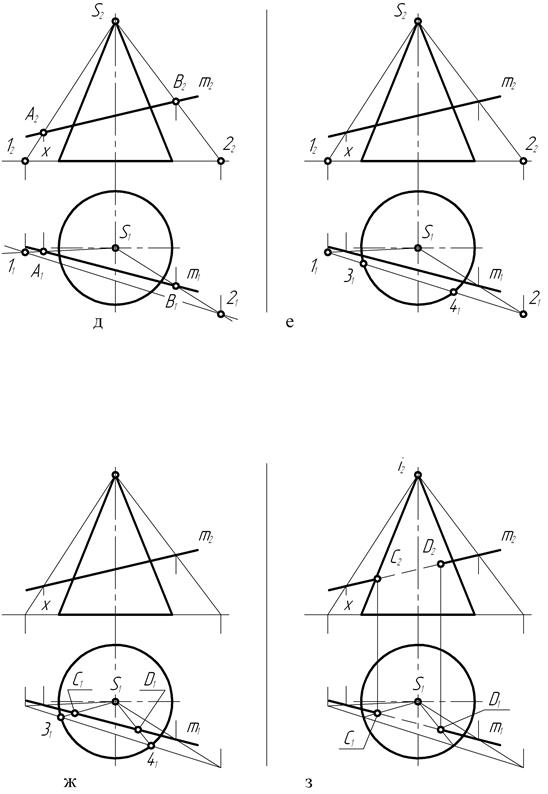
Рис. 148
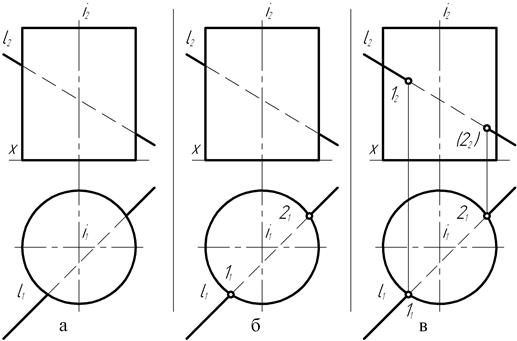
Рис. 149
Рис.150
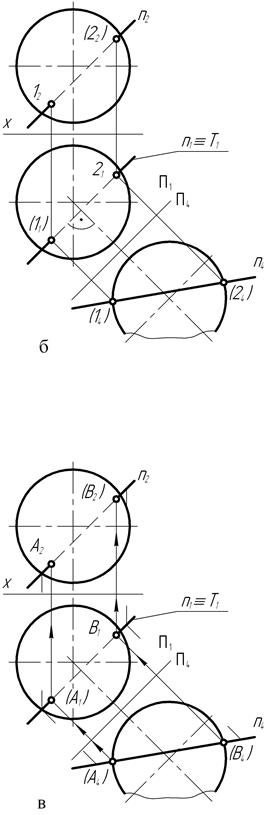
Рис. 150
А тогда представится возможность заключить прямую в секущую плоскость уровня, и фигура сечения – окружность спроецируется на соответствующую плоскость проекций без искажения – в натуральную величину.
Для осуществления подобного плана построений проведена новая ось проекций П1/П4 параллельно горизонтальной n1 проекции прямой и построена её новая n4 проекция.
В новой системе плоскостей проекций прямая n, заданная на чертеже теперь уже проекциями n1 и n4, является прямой уровня. Если теперь прямую П заключить во вспомогательную горизонтально-проецирующую плоскость Т (тау), то относительно новой П4 плоскости проекций секущая плоскость окажется плоскостью уровня. И тогда фигура сечения сферы этой плоскостью – окружность, спроецируется на плоскость проекций П4 без искажений в натуральную величину.
Диаметр этой окружности равен отрезку прямой n1 ограниченному экватором сферы.
В пересечении проекций прямой n4 и окружности сечения (рис. 150, в) определяются проекции А4 и В4 точек пересечения прямой со сферой. Их горизонтальные А1 и В1 проекции располагаются на следе T1 секущей, плоскости. Положение фронтальных A2 и B2 проекций точек определяется расположением их на фронтальной n2 проекции прямой с помощью линий связи.
Таким образом, преобразованием прямой общего положения в прямую уровня была обеспечена возможность получения графически простой проекции фигуры сечения в случае использования способа вспомогательной секущей плоскости для определения положения на чертеже проекций точек пересечения сферы с прямой общего положения.
Рассмотренные примеры построения проекций точек пересечения поверхностей вращения с прямой убедительно свидетельствуют о том, что выбор вида и расположения на чертеже вспомогательной секущей плоскости определяется не только необходимостью получения графически простых фигур сечения – треугольников, окружностей, но и возможностью построения их проекций без искажения. Последнее условие непосредственно относится к тому случаю, когда в сечении поверхности вращения плоскостью образуется окружность.
Вопросы для самопроверки
1. Изложите последовательность выполнения графических построений проекций точек пересечения прямой с поверхностью вращения в случае применения способа вспомогательной секущей плоскости.
2. Каким условием определяются выбор и расположение на чертеже вспомогательной секущей плоскости?
3. При каком положении секущей плоскости в сечении прямого цилиндра вращения образуются графически простые фигуры?
4. При каком положении секущей плоскости в сечении прямого конуса вращения образуются графически простые фигуры?
5. При каком положении секущей плоскости кривая пересечения сферы проецируется в натуральную величину?
6. На чём основано построение проекций точек пересечения проецирующей прямой с поверхностью вращения?
7. Изложите эпюрный признак принадлежности точки, прямой поверхности вращения.
2.6. Последовательность выполнения построений графического решения задачи 6 [ 1 ]
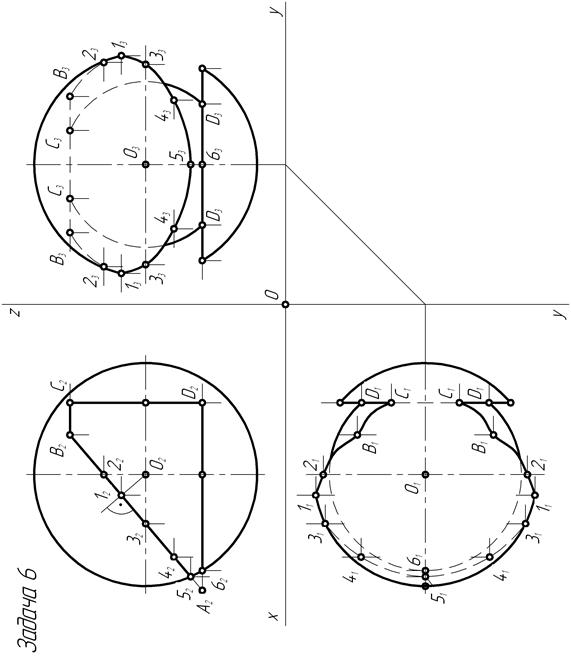
Задача – на трёхпроекционном чертеже построить недостающие проекции сквозного четырёхугольного отверстия в сфере заданного радиуса.
Графическое решение задачи начинают с того, что на листе чертежной бумаги (ватмане) формата A3 (297´420 мм) карандашом тонкими линиями выполняют рамки формата и чертежа. В правом нижнем углу длинной стороны формата располагают рамку основной надписи.
В центре поля чертежа (рис. 151) размечают и проводят две взаимно перпендикулярные прямые линии: горизонтальную и вертикальную, пересекающиеся в точке О – начале отсчета координат. Пересекающиеся прямые линии являются осями проекции Х, Y и Z .
По числовым значениям координат центра 0 сферы, взятым из таблицы 5 методических указаний [1] в зависимости от номера варианта задачи, строят его проекции. Получают трехпроекционный чертеж сферы заданного радиуса.
По числовым значениям координат строят фронтальные А2, В2, С2 и Д2 проекции вершин четырехугольника. Попарно соединив отрезками прямых проекции точек, получают на чертеже фронтальную проекцию сквозного отверстия в сфере – многоугольник, представляющий собой вырожденную проекцию линии сквозного отверстия. Такая вырожденная проекция отверстия в сфере получается только в случае пересечения ее четырьмя фронтально-проецирующими плоскостями (отсеками). В пересечении смежных отсеков проецирующих плоскостей образуются ребра А1-А2, В1-В2, С1-С2 и Д1-Д2 четырехгранника.
| Рис. 151 |
Известно, что сфера пересекается плоскостью по окружности. Поэтому линии пересечения сферы с четырехгранником представляют собой отсеки окружностей, соединенные между собой точками пересечения ребер со сферой. В зависимости от расположения секущей плоскости относительно плоскостей проекций окружность сечения проецируется в натуральную величину или в искаженном виде – в виде эллипса.
Таким образом, для построения недостающих проекций линий сквозного четырехугольного отверстия в сфере необходимо построить проекции точек пересечения каждого из ребер четырёхгранника со сферой и проекцией отсеков окружностей пересечения сферы с каждой из четырех граней.
Грань А1А2В1В2 представляет собой отсек фронтально-проецирующей плоскости. Она располагается наклонно к горизонтальной и профильной плоскостям проекций. Окружность сечения сферы этой плоскостью проецируется на них в виде эллипса. Построение проекций эллипса производят по точкам, взятым на фронтальной проекции отсека окружности сечения сферы, совпадающей с фронтальной 
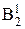
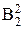
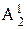проекцией грани. Из множества точек окружности выделяют на чертеже положения фронтальных проекций характерных (опорных) точек, ограничивающих большую (точка 5) и малую (точки 11 и 12) оси эллипса, расположенных на экваторе (точки 31 и 32, являющиеся точками видимости для горизонтальной плоскости проекций; точки 21 и 22, являющиеся точками видимости для профильной плоскости проекций) и главных меридианах, а также несколько произвольных точек.
Построение горизонтальных и профильных проекций точек, выделенных на фронтальной плоскости проекций, производят на основании принадлежности последних сферической поверхности. При этом исходят из того, что проекции точки, принадлежащей сферической поверхности, должны располагаться на соответствующих проекциях её параллели или меридиана.
Грани В1В2С1С2В1 и Д1Д2А1А2Д1 являются отсеками горизонтальных плоскостей уровня. Отсеки их фигур сечения – окружности, проецируются на горизонтальную плоскость проекций в натуральную величину с радиусами, равными радиусам параллелей, плоскости которых совпадают с горизонтальными плоскостями уровня. При этом одновременно определяются положения горизонтальных проекций точек пересечения рёбер В1-В2, С1-С2, Д1-Д2 со сферой. По имеющимся фронтальным и горизонтальным проекциям ребер и отсеков линий сечений строят их профильные проекции.
Грань С1С2Д1Д2С1 является отсеком профильной плоскости уровня. Отсек окружности, расположенный в этой грани, проецируется на профильную плоскость проекций в натуральную величину. Радиус отсека окружности сечения равен радиусу параллели, плоскость которой совпадает с профильной плоскостью уровня грани.
Окончательную обводку линий сквозного отверстия в сфере выполняют с учётом видимости их проекций на чертеже. Видимость проекций точек и линий сферы определяется расположением последних относительно экватора или главных меридианов. Видимые проекции линий выполняют сплошной толстой линией, а невидимые – штриховой.
Дата: 2019-02-25, просмотров: 510.
