Рассмотрим этот вопрос применительно к построению на чертежах недостающих проекций точек, расположенных на поверхностях вращения (рис. 118). При этом необходимо иметь в виду, что точки, принадлежащие поверхности вращения, располагаются только на наружных поверхностях фигур.
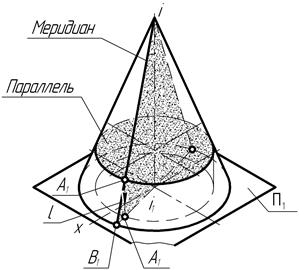
Рис. 118
Исходя из ранее сформулированного признака принадлежности точки поверхности вращения, через точку А, лежащую, например, на наружной поверхности прямого конуса вращения, можно провести только один меридиан или только одну параллель. На проекциях этих линий и должны располагаться соответствующие проекции точки поверхности вращения.
Для поверхностей, образованных вращением прямолинейной образующей (иначе их ещё называют линейчатыми поверхностями вращения), можно установить и другой признак принадлежности точки. Он состоит в том, что через точку, лежащую на линейчатой поверхности, можно провести только одну прямолинейную образующую, например, прямую l.
Исключение из этого положения составляет линейчатая поверхность однополостного гиперболоида вращения – через точку, лежащую на его поверхности, можно провести две прямолинейные образующие.
Однако для конических и цилиндрических поверхностей вращения это положение довольно часто используется для построения на чертежах этих поверхностей недостающих проекций точек.
На чертеже (рис. 119, а) заданы положения фронтальных А2 и В2 проекций точек А и В, принадлежащих цилиндру вращения.
Анализируя расположение проекций точек А и В на фронтальной П2 плоскости проекций, приходим к выводу о том, что точка А находится на видимой по отношению к плоскости П2 части поверхности цилиндра, а точка В – на невидимой, так как её фронтальная В2 проекция заключена в круглые скобки.
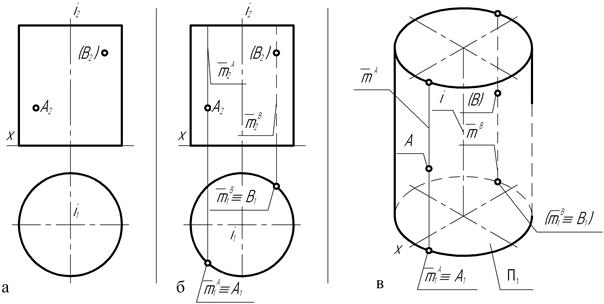
Рис. 119
Вспомним о том, что по отношению к фронтальной плоскости проекций поверхность вращения делится главной меридиональной плоскостью на две части: видимую и невидимую.
На чертеже горизонтальный след этой плоскости мысленно можно провести через проекцию i1 оси вращения параллельно оси проекций Х. То есть горизонтальный след плоскости главного меридиана совпадает с осью симметрии, параллельной оси проекций Х, окружности, являющейся горизонтальной проекцией прямого цилиндра вращения.
Следовательно, горизонтальные проекции точек А и В должны быть расположены соответственно на видимой и невидимой частях окружности – горизонтальной проекции цилиндра.
С другой стороны, на чертеже ось вращения цилиндра перпендикулярна одной из плоскостей проекций. Это означает, что цилиндрическая поверхность является проецирующей. И так как в рассматриваемом примере она является горизонтально-проецирующей поверхностью, то горизонтальная проекция прямолинейной образующей m, проведенной через любую точку поверхности, например, точку А или точку В (рис. 119, б), будет располагаться только на горизонтальной проекции прямого цилиндра – окружности, соответственно на видимой или невидимой её частях.
Исходя из проведённого анализа расположения цилиндра вращения относительно заданной системы плоскостей проекций и обозначения на чертеже видимости фронтальных проекций точек А и В, также на основании положения о том, что через точку, расположенную на поверхности цилиндра вращения, можно провести только одну образующую, проводим на фронтальной плоскости проекций через точки А2 и В2 прямые линии, параллельные проекции i2 оси вращения. Эти прямые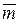 
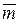2А и 2 B и представляют собой фронтальные проекции образующей m поверхности цилиндра вращения, проходящей соответственно через точки А и В.
При помощи линий связи, проведённых в направлении горизонтальной П1 плоскости проекций, определяем положение горизонтальной проекции образующей 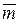1A, проходящей через точку А, на видимой части окружности и на невидимой 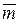1B – для образующей, проходящей через точку В.
Так как образующая поверхности является горизонтально-проецирующей прямой, то с горизонтальными проекциям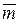и 1А и 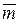1B образующей совпадают и горизонтальные А1 и В1 проекции точек А и В (рис. 119, в).
В связи с тем, что заданная на чертеже цилиндрическая поверхность вращения является горизонтально-проецирующей, задачу на построение фронтальной проекции какой-либо точки по заданной её горизонтальной проекции решить невозможно, так как горизонтальная проекция образующей поверхности представляет собой геометрическое место множества конкурирующих точек этой прямой.
На рис. 120, а представлены чертеж прямого конуса вращения и фронтальная проекция точки С, принадлежащей его поверхности. Так как фронтальная С2 проекция точки не заключена в круглые скобки, становится очевидным, что точка С располагается на видимой по отношению к П2 части конической поверхности, то есть находится между главной меридиональной плоскостью и наблюдателем.
Для определения положения на чертеже горизонтальной проекции точки (рис. 120, б) на фронтальной плоскости проекций через вершину конуса и точку С2 проведена прямая и отмечена точка I2 пересечения её с основанием конуса. Прямая I2-S2 представляет собой проекцию образующей l конической поверхности, проходящей через точку С. Затем (рис. 120, в) при помощи линии связи, проведённой через точку I2 в направлении горизонтальной плоскости проекций, определяют положение проекции I1 точки, расположенной на видимой части основания конуса.
Соединив точку I1 с проекцией S1 вершины конуса (рис. 120, г), совпадающей с проекцией i1 оси вращения, получают горизонтальную I1-S1 проекцию образующей, проходящей через точку С.
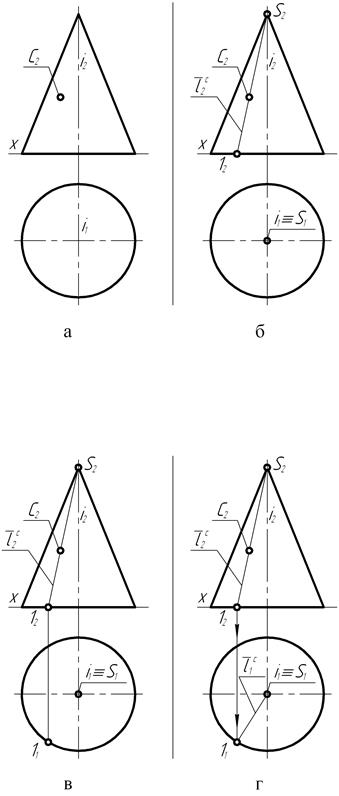
Рис. 120
Теперь на основании признака принадлежности точки С образующей конической поверхности – прямой I-S (рис. 120, д), определяют с помощью линии связи положение горизонтальной С1 проекции точки С.
И так как проекции точки С (С2, С1) располагаются на соответству-ющих проекциях образующей I-S конической поверхности, то вполне очевидным будет утверждение о принадлежности точки С заданной на чертеже поверхности прямого конуса вращения.
На рис. 120, е представлено наглядное изображение рассмотренной выше последовательности построения горизонтальной проекции точки С, принадлежащей конической поверхности, с помощью её образующей. В аналогичной последовательности осуществляется процесс построения фронтальной проекции точки конуса вращения (рис. 121, а) по заданной её горизонтальной проекции.
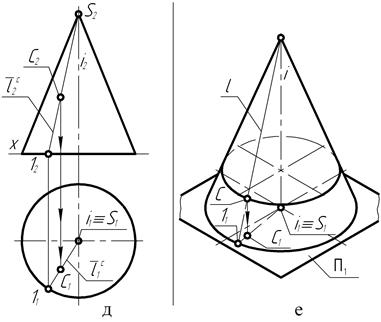
Рис. 120
Теперь уже на горизонтальной П1 плоскости проекций (рис. 121, б) через точку В1 проводят прямую I1-S1, представляющую собой горизонтальную проекцию образующей конической поверхности, проходящей через точку В. Затем (рис. 121, в) строят фронтальную I2-S2 проекцию этой образующей, расположенной на видимой части поверхности конуса, и с помощью линии связи, проведённой через точку В1 в направлении фронтальной плоскости проекций, в месте пересечения с проекцией I2-S2 образующей определяют положение точки В2, являющейся второй проекцией точки В, принадлежащей поверхности прямого конуса вращения.
Для построения недостающих проекций точек (рис. 122, а), принадлежащих поверхности вращения, можно воспользоваться и тем положением, что через точку поверхности вращения можно провести только одну параллель (рис. 122, б). Для этого через фронтальную А2 проекцию точки, принадлежащей поверхности прямого конуса вращения и расположенной на видимой части его поверхности, проводят прямую линию в направлении, перпендикулярном проекции i2 оси вращения. Отрезок этой прямой, ограниченный главным меридианом поверхности вращения, представляет собой фронтальную проекцию параллели точки А. Причём длина этого отрезка равна натуральной величине диаметра окружности параллели. Осью вращения этот отрезок делится пополам и равен, соответственно, натуральной величине радиуса окружности параллели. На основании этого положения строят горизонтальную проекцию параллели точки А.
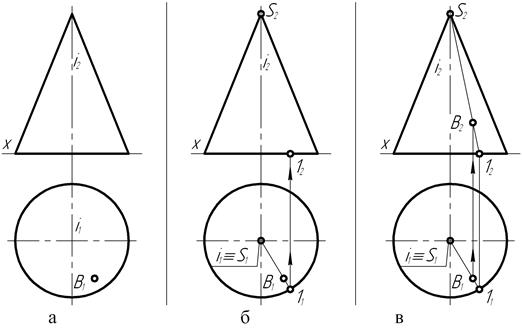
Рис. 121
Затем (рис. 122, в) через проекцию А2 проводят линию связи до пересечения с горизонтальной проекцией параллели, расположенной на видимой части поверхности конуса.
Получают недостающую – горизонтальную А1 проекцию точки А, принадлежащей поверхности прямого конуса вращения.
На рис. 122, г представлено наглядное изображение рассмотренной выше последовательности построения недостающей проекции точки, принадлежащей конической поверхности вращения, с помощью ее параллели.
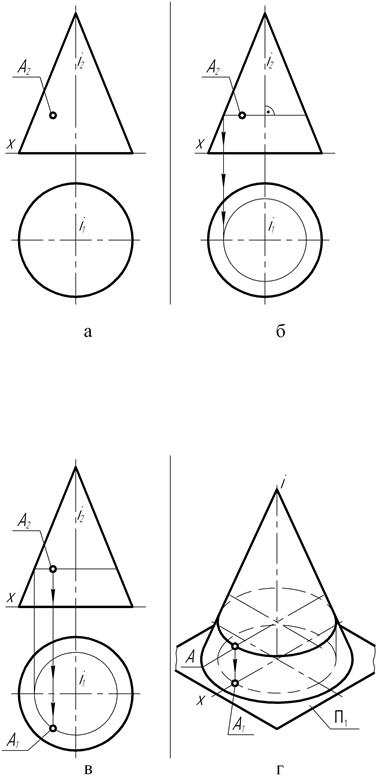
Рис. 122
Рассмотренный пример построения недостающей проекции точки с помощью её параллели является иллюстрацией эпюрного признака принадлежности точки поверхности вращения: проекции точки располагаются на соответствующих проекциях её параллели.
На рис. 123 представлена последовательность построения на чертеже сферической поверхности недостающей – горизонтальной проекции точки В, принадлежащей этой поверхности.
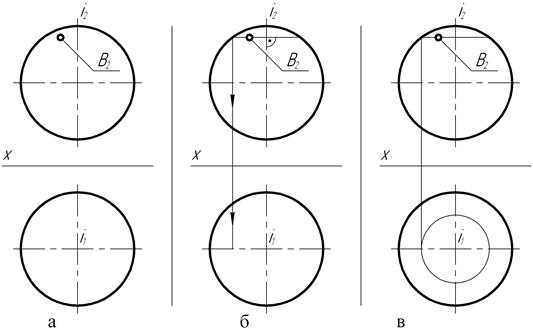
Рис. 123
Вначале следует остановиться на рассмотрении вопроса о видимости точек, расположенных на сфере, относительно заданной системы плоскостей проекций. Вспомним установленное ранее положение о том, что плоскость экватора поверхности, то есть параллели с наибольшим радиусом вращения, определяет видимость проекций точек на горизонтальной плоскости проекций, а главная меридиональная плоскость поверхности определяет видимость проекций точек на фронтальной плоскости проекций.
На чертеже (рис. 123, а) фронтальная В2 проекция точки не заключена в круглые скобки, то есть фронтальная проекция точки является видимой. Это значит, что точка В находится на той части поверхности сферы, которая располагается перед главной меридиональной плоскостью.
С другой стороны, фронтальная В2 проекция точки располагается на чертеже над плоскостью экватора сферы, а поэтому ее горизонтальная проекция должна быть видимой, и, как это было установлено выше, должна находиться перед главной меридиональной плоскостью.
Теперь (рис. 123, б) строят вначале фронтальную проекцию параллели точки В, а затем (рис. 123, в) и ее горизонтальную проекцию.
При помощи линии связи (рис. 123, г), проведенной через проекцию В2 точки, определяют положение ее горизонтальной В1 проекции.
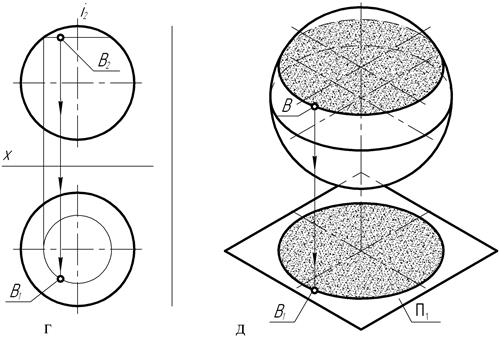
Рис. 123
На рис. 123, д представлено наглядное изображение рассмотренной выше последовательности построения недостающей проекции точки, принадлежащей сферической поверхности, с помощью ее параллели.
На рис. 124, а, б, в показана последовательность построения на чертеже сферы недостающей, теперь уже фронтальной, проекции точки А.
Таким образом, представленные выше примеры построения недостающих проекций точек, расположенных на поверхностях вращения, подтверждают вывод о том, что установленный при рассмотрении особенностей образования поверхностей вращения эпюрный признак принадлежности точек поверхности позволяет однозначно определять на чертежах положения их проекций. Выбор того или иного способа построения проекций точек, принадлежащих поверхностям вращения, определяется в основном трудоемкостью или точностью выполнения графических построений.
Учитывая особую важность эпюрного признака принадлежности точки поверхности для изучения последующих вопросов темы «Поверхности вращения», напомним его еще раз: проекции точки, принадлежащей поверхности вращения, должны обязательно располагаться на одноименных проекциях – образующей, меридиана или параллели, проходящих через эту точку.
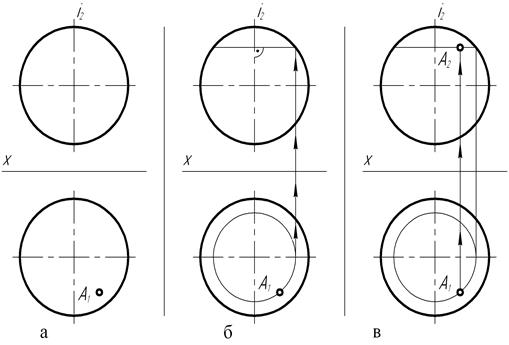
Рис. 124
Вопросы для самопроверки
1. Какая поверхность называется поверхностью вращения?
2. Какие линии используются в качестве образующей для поверхности вращения?
3. Как называется поверхность вращения, имеющая в качестве образующей прямую линию:
- расположенную параллельно оси вращения;
- пересекающуюся с осью вращения;
- скрещивающуюся с осью вращения?
4. Как образуется сферическая поверхность?
5. Какая поверхность называется тором?
6. Какая поверхность называется глобоидом?
7. Что такое параболоид вращения?
8. Что такое эллипсоид вращения?
9. Как образуется сфероид вращения?
10. Что такое гиперболоид вращения? Какие существуют его разновидности?
11. Что такое параллель поверхности вращения?
12. Сколько параллелей можно провести через точку на поверхности вращения?
13. В каком случае параллель поверхности вращения проецируется в натуральную величину? Что представляет собой в этом случае вторая проекция параллели и как она располагается на чертеже относительно проекции оси вращения?
14. Что такое экватор поверхности вращения? Каким образом определяется видимость проекций точек, расположенных, например, на сферической поверхности, относительно экватора?
15. Что такое меридиан поверхности вращения?
16. Сколько меридианов можно провести через точку, расположенную на поверхности вращения?
17. Что такое главный меридиан поверхности вращения?
18. Что такое главная меридиональная плоскость?
19. Каким образом определяется видимость проекций точек, расположенных, например, на поверхности прямого конуса вращения, относительно главной меридиональной плоскости?
20. Какая поверхность называется прямым цилиндром вращения?
21. Является ли поверхность прямого цилиндра вращения проецирующей? Почему?
22. Какая поверхность называется прямым конусом вращения?
23. Является ли поверхность прямого конуса вращения проецирующей? Почему?
24. Сформулируйте признак принадлежности точек поверхности вращения.
25. Сформулируйте эпюрный признак принадлежности точки поверхности вращения.
26. Если на чертеже проекции точки не располагаются на одноименных проекциях образующей, меридиана или параллели поверхности вращения, то принадлежит ли эта точка поверхности?
27. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на поверхности прямого цилиндра вращения?
28. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на поверхности прямого конуса вращения?
29. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на поверхности прямого глобоида?
30. Каким образом можно измерить на чертеже диаметр параллели произвольной точки, расположенной на сферической поверхности?
Дата: 2019-02-25, просмотров: 377.
