Выше отмечалось, что способ вспомогательных секущих плоскостей применяется в тех случаях, когда при пересечении плоскостью поверхностей вращения в сечении образуются графически простые линии - прямые или окружности (рис. 153).

В целом графические построения проекций точек кривой взаимного пересечения поверхностей вращения осуществляются в следующей последовательности:

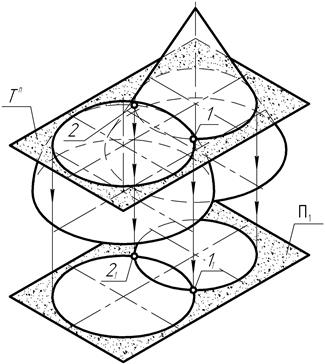
Рис. 153

- выбирают положение вспомогательной секущей плоскости таким, чтобы в сечении каждой из поверхностей вращения получались графически простые линии - прямые или окружности;

- строят проекции линий сечения каждой из поверхностей вращения одной и той же секущей плоскостью;

- выявляют точки пересечения одноименных проекций линий сечения; плоскости или соответствующей поверхности вращения строят их недостающие проекции;

- точки пересечения одноименных проекций линий сечения являются общими для обеих поверхностей вращения и, следовательно, принадлежат кривой их взаимного пересечения;

- на основании принадлежности точек кривой пересечения секущей плоскости или соответствующей поверхности вращения строят их недостающие проекции.

Подобным образом определяют положения проекций необходимого количества произвольных точек кривых взаимного пересечения поверхностей вращения.

В качестве вспомогательных секущих плоскостей чаще всего используются плоскости частного положения – проецирующие или плоскости уровня. В некоторых случаях успешно применяются и плоскости общего положения. При этом необходимо иметь в виду, что выбор вида и положения вспомогательной секущей плоскости определяется только одним условием – обе поверхности должны пересекаться одной и той же секущей плоскостью по графически простым линиям. Поэтому очень важно иметь представление о том, что, например, в сечении цилиндра вращения графически простые линии образуются только в случае пересечения его плоскостью, параллельной или перпендикулярной оси вращения (рис. 154).

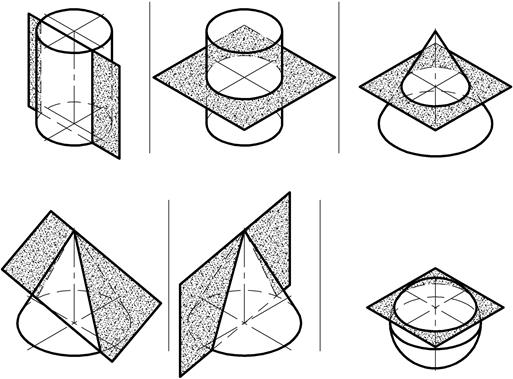
Рис. 154

В сечении конуса вращения образуются графически простые линии только при пересечении его плоскостью, перпендикулярной оси вращения или проходящей через вершину.

Сферическая поверхность вращения при любом положении секущей плоскости пересекается по окружности. Но использовать в качестве секущих целесообразно лишь плоскости уровня. Только в этом случае кривая сечения – окружность – проецируется на соответствующую плоскость проекций без искажения, в натуральную величину.

На чертеже (рис. 155, a) прямой конус вращения пересекается с полусферой. Построение проекций линии взаимного пересечения поверхностей начинают, прежде всего, с определения положения на чертеже опорных точек – экстремальных и точек видимости.

По чертежу устанавливают, что пересекающиеся поверхности вращения имеют общую плоскость симметрии, расположенную параллельно фронтальной плоскости проекций. Это обстоятельство позволяет сделать вывод о том, что, во-первых, плоскость симметрии фигур совпадает с положениями главных меридиональных плоскостей каждой из поверхностей вращения. Тогда горизонтальные проекции точек кривой пересечения окажутся расположенными симметрично относительно горизонтального следа главной меридиональной плоскости, являющейся общей для обеих фигур.

Фронтальные проекции точек кривой пересечения будут совпадать, так как в этом случае они являются конкурирующими по отношению к фронтальной плоскости проекций. Причём проекции точек, расположенных перед главной меридиональной плоскостью фигур, будут видимыми на фронтальной плоскости проекций, а расположенных за ней – невидимыми.

Рис. 155

Горизонтальные проекции точек кривой пересечения являются видимыми, так как это обусловлено видом и расположением на чертеже заданных поверхностей вращения. Значит, кривая пересечения поверхностей не содержит опорных точек видимости. А поэтому необходимо будет определять положения на чертеже лишь экстремальных точек кривой пересечения.

И во-вторых, фронтальные проекции фигур представляют собой главные меридианы поверхностей вращения, а они, как это следует из чертежа (рис. 155, б) пересекаются в точке А₂. Горизонтальная А₁ проекция точки располагается на следе главной меридиональной плоскости.

Точка А, определенная на чертеже фронтальной А₂ и горизонтальной А₁ проекциями, является общей для обеих поверхностей вращения и относится к числу самых высоких точек кривой пересечения.

Таким образом, положение высшей опорной точки А кривой пересечения (рис. 156) определено, по сути дела, с помощью секущей плоскости, совпадающей с плоскостью симметрии фигур и являющейся главной меридиональной плоскостью заданных поверхностей вращения.

То обстоятельство, что основания фигур располагаются непосредственно в горизонтальной плоскости проекций (рис. 157), позволяет выявить положения низших точек В и С кривой пересечения.

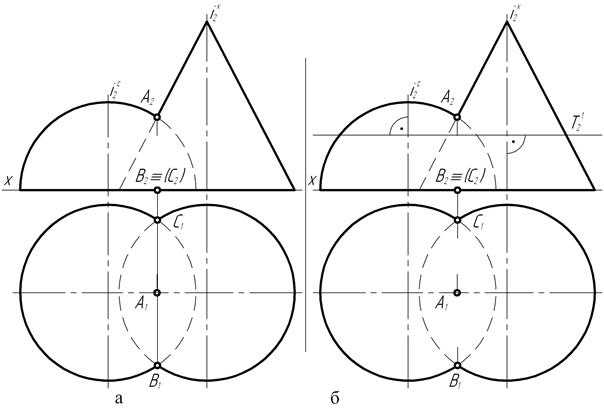
Действительно, точки В₁ и С₁ пересечения горизонтальных проекций основания фигур (рис. 158, а) принадлежат обеим поверхностям вращения и являются низшими точками кривой пересечения, так как их фронтальные В₂ и С₂ проекции располагаются непосредственно на оси проекций Х.

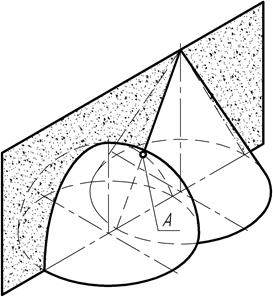
Рис. 156

В то же время, по отношению к наблюдателю точка В (В₁, В₂) является самой близкой, а точка С (С₁, С₂) – самой дальней.

Выше отмечалось, что кривая взаимного пересечения поверхностей вращения не имеет точек видимости, поэтому все остальные точки, кроме точек А, В и С, относятся к числу произвольных и для определения положения их проекций на чертеже (рис. 158, б) используют вспомогательную горизонтальную секущую плоскость Т (тау). Только при таком положении секущей плоскости (рис. 159) предоставляется возможность получить в сечении обеих поверхностей вращения графически простые линии – окружности.

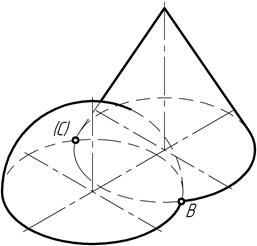
Рис. 157

Рис. 158

Действительно, выбор в качестве секущей горизонтальной плоскости уровня обусловлен тем обстоятельством, что оси вращения фигур располагаются на чертеже перпендикулярно горизонтальной плоскости проекций. Тогда секущая плоскость уровня окажется расположенной перпендикулярно оси вращения каждой из фигур. А именно при таком положении секущей плоскости в сечении конуса и сферы образуются окружности, представляющие параллели этих поверхностей. В пересечении параллелей друг с другом выявляются точки, например, 1 и 2, принадлежащие обеим поверхностям вращения и относящиеся к числу произвольных точек кривой пересечения.

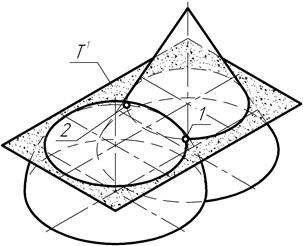
Рис. 159

На чертеже (рис. 160, а) фронтальный Т¹₂ след первой горизонтальной секущей плоскости проводят несколько ниже фронтальной А₂ проекции высшей точки кривой пересечения, и строят горизонтальные проекции параллелей конуса и полусферы. В пересечении горизонтальных проекций параллелей (рис. 160, б) образуются точки 1₁ и 2₁, принадлежащие обеим фигурам и относящиеся к числу произвольных точек кривой пересечения. Их фронтальные 1₁ и 2₂ проекции располагаются на следе Т¹₂ секущей плоскости. Подобным образом на чертеже (рис. 161, а) определяют положения некоторого количества проекций произвольных точек кривой пересечения. Соединив затем (рис. 161, б) плавной кривой линией одноименные проекции точек, получают фронтальную и горизонтальную проекции кривой пересечения полусферы с прямым конусом вращения.

Таким образом, вид и расположение проекций поверхностей вращения предопределили возможность использования вспомогательных секущих плоскостей для определения положения проекций произвольных точек кривой их взаимного пересечения.

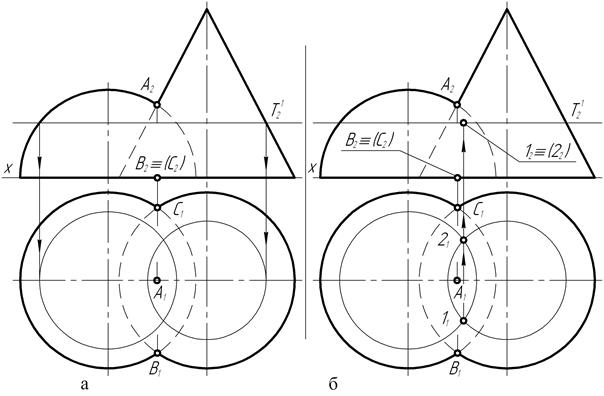
Рис. 160

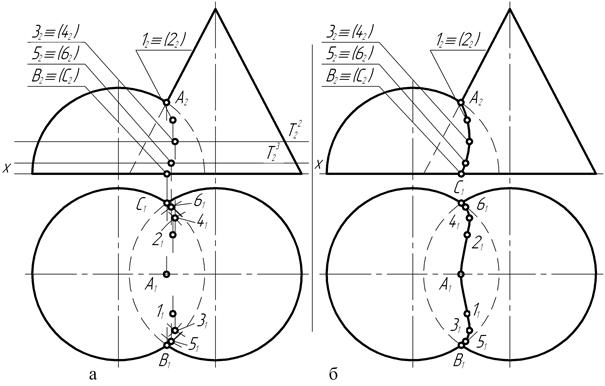
Рис. 161

Вместе с тем рассмотренный пример построения проекций линии взаимного пересечения поверхностей вращения позволяет сформулировать условие, ограничивающее использование в качестве секущих – плоскостей уровня: оси вращения обеих фигур должны располагаться перпендикулярно одной из плоскостей проекций.

В том случае, когда при пересечении обеих поверхностей вращения одной секущей плоскостью невозможно получить в сечениях графически простые линии – прямые или окружности, применяется способ вспомогательных секущих сфер.