На рис. 128, а представлен чертеж прямого цилиндра вращения, который пересекается горизонтальной секущей плоскостью Т (тау). На чертеже секущая плоскость задана фронтальным Т2 следом, расположенным перпендикулярно фронтальной i2 проекции оси вращения цилиндра. В результате этого в сечении образуется параллель цилиндрической поверхности, а так как ось вращения цилиндра перпендикулярна горизонтальной плоскости проекций, то горизонтальная проекция параллели – окружность – совпадает с горизонтальной проекцией контура цилиндрической поверхности.
Таким образом, линия пересечения цилиндра плоскостью, расположенной перпендикулярно оси его вращения, представляет собой окружность.
На чертеже (рис. 129) тот же цилиндр вращения пересекается горизонтально-проецирующей плоскостью Ө (тэта), заданной на чертеже горизонтальным Ө1 следом. Проецирующая плоскость параллельна оси вращения цилиндра. Поэтому она пересекает цилиндрическую поверхность по её образующим прямым, горизонтальные проекции которых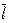 
1 и 
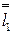совпадают с точками пересечения следа Ө1 секущей плоскости с проекцией контура цилиндра – окружностью. Фронтальные проекции образующих 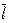2 и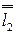 
располагаются параллельно проекции i2 оси вращения. И так как образующая 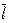располагается на невидимой части цилиндра, ее фронтальная 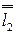проекция выполняется на чертеже штриховой линией.
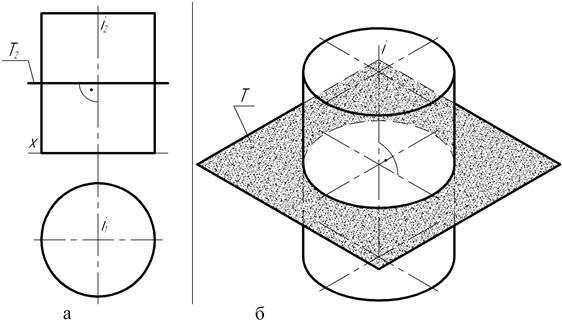
Рис. 128
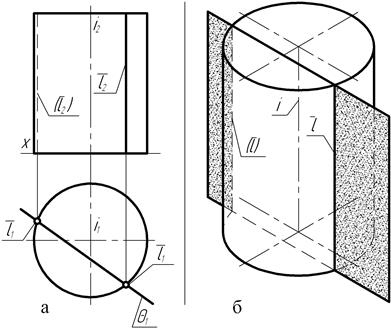
Рис. 129
Таким образом, при пересечении цилиндрической поверхности плоскостью, расположенной параллельно оси вращения, в сечении образуются прямые линии. В рассматриваемом примере фигура сечения представляет собой прямоугольник.
На чертеже (рис. 130, а) прямой цилиндр вращения пересекается с фронтально-проецирующей плоскостью λ (лямбда), расположенной под некоторым углом к оси вращения. Известно, что в этом случае линия сечения представляет собой эллипс – плоскую кривую линию. Построение проекций кривой пересечения начинают с определения на чертеже проекций опорных точек: экстремальных и точек видимости. Прежде всего анализируют расположение заданных геометрических фигур относительно друг друга и относительно плоскостей проекций. Так как секущая плоскость является фронтально-проецирующей, на чертеже уже имеется фронтальная проекция кривой пересечения, представляющая собой отрезок прямой – следа секущей плоскости, ограниченный точками А2 и В2 пересечения следа λ2 с главным меридианом прямого цилиндра
(рис. 130, б). Их горизонтальные проекции А1 и В1 располагаются на горизонтальном следе главной меридиональной плоскости. Точки:
А (А1, А2) и В (В1, В2) относятся к числу опорных точек кривой пересечения, так как они являются соответственно самой низшей – точка А и самой высшей – точка В, точками кривой пересечения. С другой стороны, точка А кривой пересечения по отношению к наблюдателю является самой левой, а точка В – самой правой.
В связи с тем, что точки кривой пересечения располагаются только на наружной цилиндрической поверхности, являющейся проецирующей по отношению к горизонтальной плоскости проекций, горизонтальная проекция эллипса совпадает с горизонтальной проекцией контура цилиндра – окружностью. Поэтому для выявления конфигурации проекций кривой пересечения возникла необходимость построения третьей – профильной проекции цилиндрической поверхности. Ее главный меридиан представляет собой прямоугольник, так как в этом случае главная меридиональная плоскость, проходящая через ось вращения цилиндра, располагается параллельно теперь уже профильной плоскости проекций.
При помощи линий связи построены профильные А3 и В3 проекции высшей и низшей опорных точек.
Известно, что эллипс имеет большую и малую оси, пересекающиеся под прямым углом, и что точка их пересечения делит оси пополам.
И, наконец, точки кривой располагаются симметрично относительно большой и малой осей эллипса. Проекции прямой А-В (А2-В2, А1-В1) представляют собой проекции на чертеже большой оси эллипса. Прямая А2-В2, соответствующая натуральной величине большой оси эллипса, пересекается с проекцией i2 оси вращения в точке, представляющей собой проекции
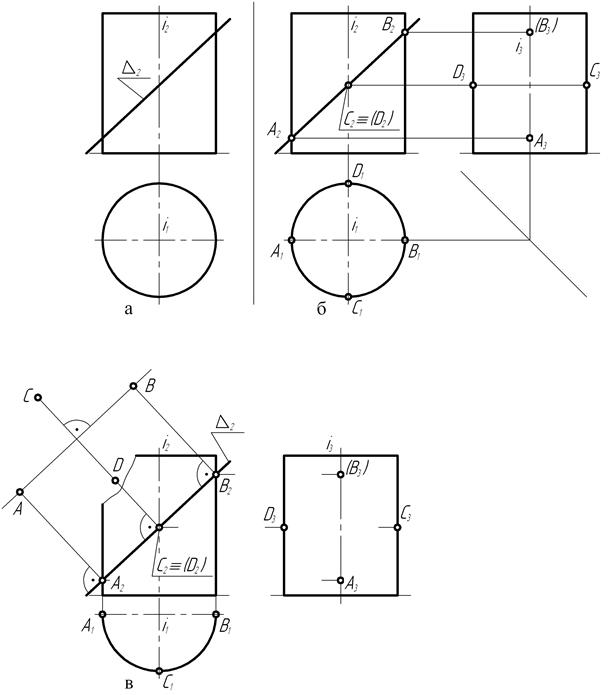
Рис. 130
двух конкурирующих точек С2 и Д2, ограничивающих по длине малую ось эллипса. Их горизонтальные проекции С1и Д1 располагаются соответственно на видимой и невидимой частях цилиндра.
Проекция прямой С1-Д1 соответствует натуральной величине малой оси эллипса, а точки С и Д являются соответственно самой ближней и самой дальней по отношению к наблюдателю опорными точками кривой пересечения.
Профильные проекции точек С и Д должны лежать на главном меридиане цилиндра, а положение на чертеже проекций С3 и Д3 определено с помощью линии связи, проведённой через проекции С2 и Д2 в направлении, параллельном оси проекций Х.
По отношению к профильной плоскости проекций главная меридиональная плоскость также делит цилиндр на видимую и невидимую части. Точки С и Д, лежащие в этой плоскости, являются по отношению к профильной плоскости проекций опорными точками кривой пересечения – точками видимости. Поэтому профильные проекции точек кривой пересечения, расположенные на чертеже выше точек С3 и Д3, будут невидимыми, а ниже их – видимыми.
Остальные точки кривой пересечения прямого цилиндра вращения с фронтально-проецирующей плоскостью относятся к числу произвольных точек, и положение их проекций на чертеже можно без особых трудностей определить с помощью линий связи, выделив предварительно положения фронтальных или горизонтальных проекций этих точек.
В связи с тем, что секущая плоскость является проецирующей, предоставляется возможность построения натурального вида сечения преобразованием проецирующей плоскости в плоскость уровня (рис. 130, в).
Опуская выполнение некоторых построений преобразования проецирующей плоскости в плоскость уровня, на фронтальной плоскости проекций параллельно следу λ2 секущей плоскости проведена прямая и на ней отложена натуральная величина отрезка А-В – большой оси эллипса, равная проекции А2-В2. Перпендикулярно отрезку А-В в точке, делящей его пополам, проведена прямая и на ней отложен отрезок С-Д, представляющий собой натуральную величину малой оси эллипса, равный отрезку С1-Д1.
Затем (рис. 130, г), на чертеже обозначены положения фронтальных проекций некоторых произвольных точек кривой пересечения. С помощью линий связи определены их положения на горизонтальной и профильной плоскостях проекций. Затем на прямой А-В построены натуральные величины отрезков, соединяющих симметричные точки кривой пересечения, взятые с горизонтальной плоскости проекций. Подобным приёмом (рис. 130, д) построено некоторое количество произвольных точек кривой
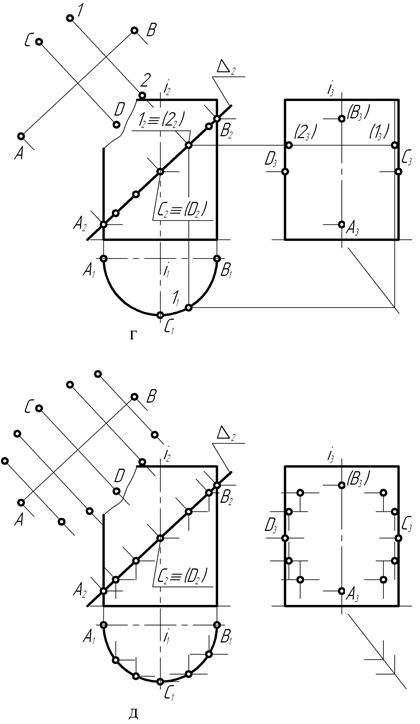
Рис. 130
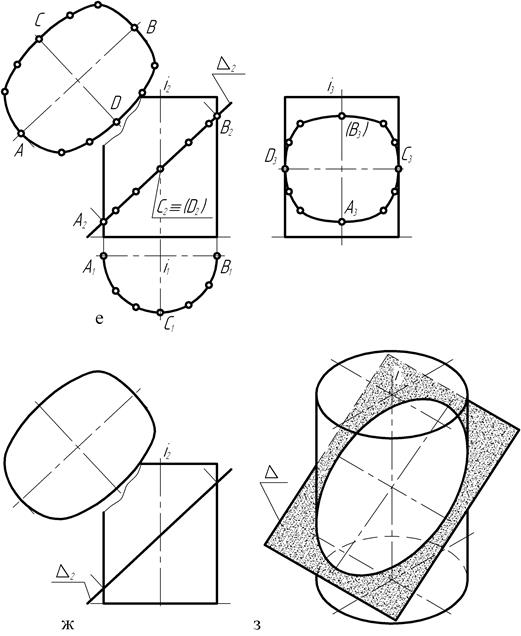
Рис. 130
пересечения и отмечена их видимость на соответствующих плоскостях проекций.
Соединив (рис. 130, е) плавной линией по лекалу профильные проекции точек, получают вырожденную проекцию кривой пересечения прямого цилиндра вращения с фронтально-проецирующей плоскостью, представляющую собой искажённую проекцию эллипса. На этом же чертеже представлен натуральный вид кривой пересечения.
Таким образом (рис. 130, ж, з) при пересечении поверхности прямого цилиндра плоскостью, расположенной под некоторым углом к оси вращения, в сечении образуется эллипс. В связи с тем, что секущая плоскость является проецирующей, проекции кривой были построены лишь на основании эпюрного признака принадлежности точки поверхности вращения, без использования способа вспомогательных секущих плоскостей.
Построение проекций линий пересечения прямого конуса вращения (рис. 131, а) с фронтально проецирующей плоскостью å, проходящей через его вершину S, осуществляется следующим образом. На фронтальной плоскости проекций (рис. 131, б) отмечают конкурирующие точки А2,В2 пересечения следа S2 секущей плоскости с проекцией основания конуса. При помощи линий связи строят их горизонтальные проекции: А1, В1.
Прямая А1-В1, по сути дела, есть не что иное, как горизонтальный å1 след фронтально-проецирующей плоскости S.
Точки А (А1, А2) и В (В1, В2) располагаются на конической поверхности и поэтому каждую из них можно соединить прямой линией с вершиной конуса S (рис. 131, в). Тогда прямые SA (S1A1, S2A2) и SB (S1B1, S2B2) будут представлять собой образующую конической поверхности, проходящей через точку А или точку В, и на этом основании можно сделать вывод о том, что при пересечении прямого конуса вращения с плоскостью, проходящей через его вершину, в сечении образуется треугольник.
На чертеже (рис. 132) прямой конус вращения пересекается горизонтально-проецирующей плоскостью, проходящей через ось вращения.
Горизонтальный Т1 след секущей плоскости (рис. 132, б) пересекает горизонтальную проекцию основания конуса – окружность в точках А1 и В1. Их фронтальные проекции должны располагаться на оси проекции Х, а положения определяются с помощью линий связи. Причём фронтальная В2 проекция точки будет невидимой, так как она располагается на невидимой части конической поверхности. Поэтому проекция S2B2 образующей поверхности конуса, проходящей через точку В, на чертеже выполнена штриховой линией. В сечении получается треугольник ASB, представляющий собой меридиан прямого конуса вращения (рис. 132, в).
В случае пересечения прямого конуса вращения (рис. 133, а) горизонтальной секущей плоскостью q (тэта) в сечении образуется окружность, представляющая собой параллель конической поверхности. Это объясняя-
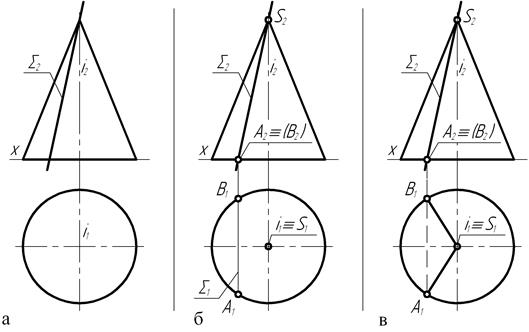
Рис. 131
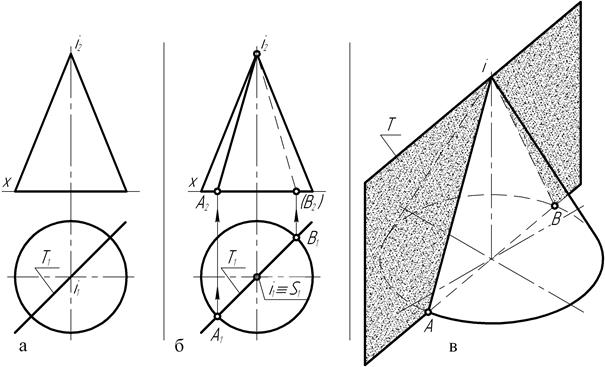
Рис. 132
ется тем, что ось вращения конической поверхности располагается на чертеже перпендикулярно горизонтальной плоскости проекций. Тогда фронтальная i2 проекция оси вращения на чертеже перпендикулярна оси проекций C. В свою очередь, фронтальный след q2 горизонтальной секущей плоскости на чертеже должен располагаться параллельно оси C. Поэтому след q2 секущей плоскости проходит перпендикулярно проекции i2 оси вращения. Тогда отрезок следа q2 секущей плоскости, находящийся внутри главного меридиана прямого конуса, есть фронтальная проекция параллели поверхности. Для построения горизонтальной проекции этой параллели отмечают точку 12 пересечения следа q2 с главным меридианом – одной из сторон треугольника, и с помощью линии связи определяют расположение её горизонтальной 11 проекции на следе главной меридиональной плоскости. Затем радиусом, равным отрезку 11-i1, проводят окружность, представляющую собой горизонтальную проекцию линии сечения прямого конуса вращения плоскостью, проведённой перпендикулярно оси вращения.
При пересечении конической поверхности (рис. 134) плоскостью, параллельной оси вращения, получается кривая линия-гипербола. На чертеже прямой конус вращения пересекается фронтальной плоскостью S, которая по отношению к горизонтальной плоскости проекций является проецирующей. Горизонтальный след S1 фронтальной секущей плоскости располагается на чертеже параллельно оси проекций C. На следе S1 находится горизонтальная проекция кривой пересечения, а на фронтальную плоскость проекций кривая пересечения спроецируется в натуральную величину.
Построение фронтальной проекции кривой пересечения начинают с выявления положения горизонтальных проекций опорных точек. К ним, в первую очередь, относятся точки А1 и В1 пересечения следа S1 с проекцией контура основания конуса – окружностью. Их фронтальные проекции должны располагаться на оси проекций C, а положения определяются с помощью линий связи. Точка А (А1, А2) является самой левой, а точка В (В1, В2) – самой правой опорными точками прямой пересечения.
Для прямого конуса вращения, заданного на чертеже, самая высокая точка кривой пересечения должна иметь наименьший радиус параллели. Точка С1 является горизонтальной проекцией такой точки. Положение фронтальной С2 проекции установлено с помощью параллели этой точки.
Остальные точки прямой пересечения (рис. 134, г, д) относятся к числу произвольных. Положения фронтальных проекций произвольных точек кривой пересечения установлены с помощью параллелей, на основании эпюрного признака принадлежности точки поверхности вращения. Так как секущая плоскость пересекает видимую часть конической поверхности, фронтальные проекции всех точек кривой сечения являются видимыми.
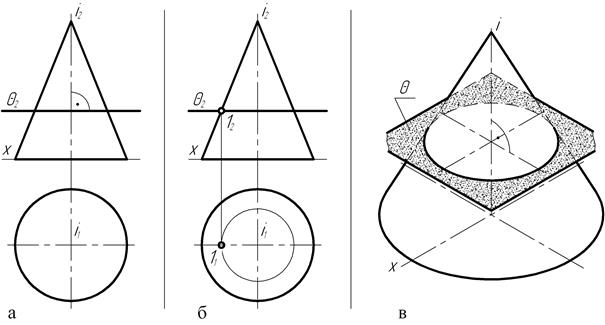
Рис. 133
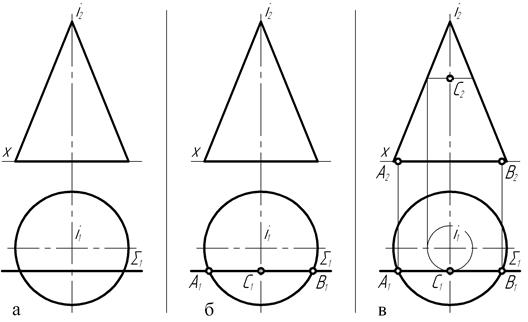
Рис. 134
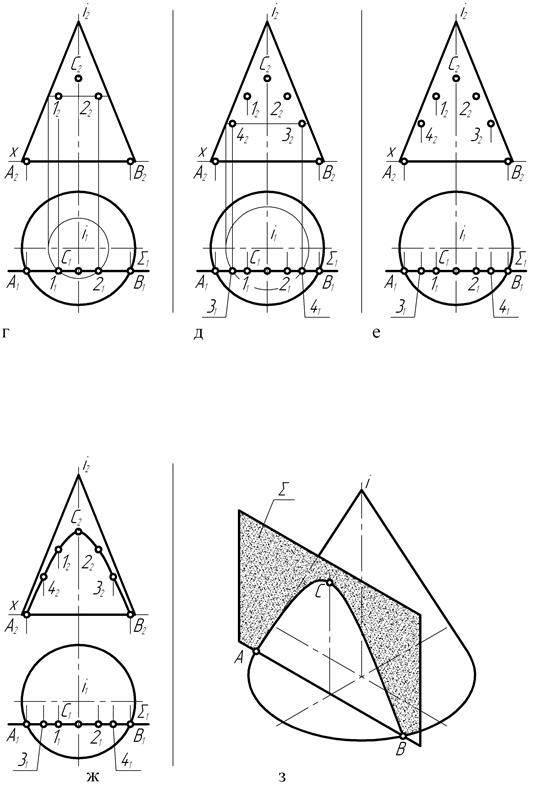
Рис. 134
Соединив (рис. 134, ж) плавной кривой линией фронтальные проекции точек, получают фронтальную проекцию сечения – гиперболу.
В случае пересечения конической поверхности (рис. 135, а) плоскостью, параллельной её прямолинейной образующей, в сечении получается кривая линия – парабола.
На чертеже секущая плоскость l (лямбда), пересекающая поверхность прямого конуса вращения, является фронтально-проецирующей. Отрезок А2-В2, (С2) фронтального l2 следа секущей плоскости (рис. 135, б), находящийся внутри контура главного меридиана конической поверхности, представляет собой фронтальную проекцию кривой пересечения.
Построения горизонтальных проекций точек кривой пересечения не вызывает особых затруднений. На основании эпюрного признака принадлежности точек поверхности прямого конуса эти построения очень легко выполняются.
Однако вначале на чертеже (рис. 135, в) определяют положение опорных точек кривой пересечения. Вполне очевидно, что к таким точкам следует отнести прежде всего конкурирующие точки В и С, а также точку А. Точка А является самой высшей, а точки В и С – самыми низшими точками кривой пересечения.
Горизонтальная А1 проекция точки А должна располагаться на следе главной меридиональной плоскости. Проекции В1 и С1 – на горизонтальной проекции основания конуса – окружности. Причём точка С располагается на невидимой части конической поверхности, а точка В – на видимой. Из них точка С является самой дальней, а точка В – самой близкой по отношению к наблюдателю.
Остальные точки кривой пересечения являются произвольными. Для построения горизонтальных проекций произвольных точек вначале на чертеже выделяют некоторые из них на следе l2 секущей плоскости, между проекциями высшей и низшими опорными точками. При этом необходимо иметь в виду, что при заданном расположении геометрических фигур на чертеже кривая пересечения имеет ось симметрии, лежащую в главной меридиональной плоскости. Поэтому произвольные точки кривой пересечения являются конкурирующими по отношению к фронтальной плоскости проекций и их проекции совпадают.
На рис. 135, г, д, е представлен процесс построения горизонтальных проекций некоторых произвольных точек кривой пересечения с помощью параллелей.
И, наконец (рис. 135, ж, з), соединив плавной кривой линией горизонтальные проекции точек, получают горизонтальную проекцию кривой пересечения прямого конуса вращения с фронтально-проецирующей секущей плоскостью.
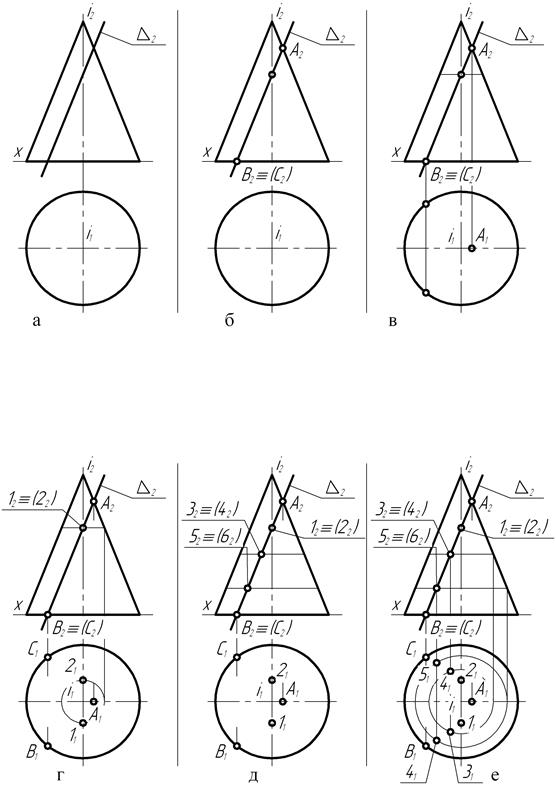
Рис. 135
Обратите внимание на положение проекций конкурирующих точек 1 и 2 кривой пересечения. Их фронтальные проекции 12 и 22 располагаются на проекции i2 оси вращения. Для данного чертежа эти точки кривой пересечения являются произвольными. Но если возникает необходимость в построении профильной проекции кривой пересечения, точки 1 и 2 будут относиться уже к числу опорных точек. Они определяют видимость кривой пересечения на профильной плоскости проекций.
На чертеже (рис. 136) прямой конус вращения пересекается с фронтально-проецирующей плоскостью Т (тау), расположенной под некоторым углом к оси вращения. След Т2 секущей плоскости располагается при этом не параллельно прямолинейной образующей конической поверхности. В этом случае кривая пересечения представляет собой эллипс.
В связи с тем, что секущая плоскость является проецирующей, на чертеже уже имеется одна из проекций кривой пересечения, ограниченная отрезком А2-В2 следа Т2 секущей плоскости, находящегося внутри главного меридиана конической поверхности. Тогда горизонтальные А1 и В1 проекции точек располагаются на следе главной меридиональной плоскости.
В главной меридиональной плоскости располагается ось симметрии кривой пересечения прямого конуса вращения. Это значит, что помимо точек А и В, все другие точки кривой пересечения являются конкурирующими, а поэтому их фронтальные проекции совпадают.
Известно также, что большая и малая оси эллипса пересекаются друг с другом под прямым углом и точка пересечения делит оси пополам. Отрезок А2-В2 представляет собой натуральную длину большой оси эллипса. Если разделить его пополам известным приёмом (рис. 136, в), то на чертеже выявится положение фронтальных проекций точек 12 и 22, ограничивающих по длине малую ось эллипса.
С помощью параллели (рис. 136, г) определяется положение на чертеже горизонтальных 11 и 21 проекций этих точек. А сам отрезок 11-21 есть не что иное, как натуральная величина малой оси эллипса.
Точки А, В, 1 и 2 относятся к числу опорных точек кривой пересечения. Действительно, рассматривая положение их проекций на чертеже, убеждаемся в том, что точка А – самая высшая, точка В – самая низшая, точка 1– самая близкая и точка 2 – самая дальняя.
Остальные точки кривой пересечения можно отнести к числу произвольных точек. Для построения их проекций на чертеже, вначале выделяют положение их фронтальных проекций на следе Т2 секущей плоскости. Например, проекция конкурирующих точек 32 и 42 (рис. 136, д, е). Затем с помощью параллели поверхности вращения строят их горизонтальные 31 и 41 проекции.
Аналогичным приёмом (рис. 136, ж, з) определяют положения на чертеже других произвольных точек, например, точек 5 (52, 51) и 6 (62, 61).
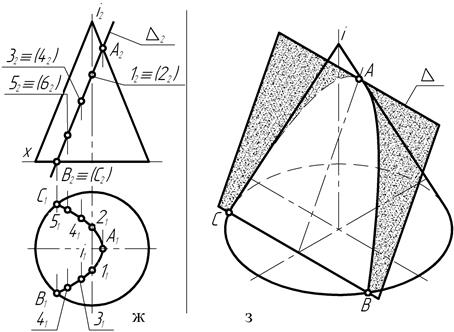
Рис. 135
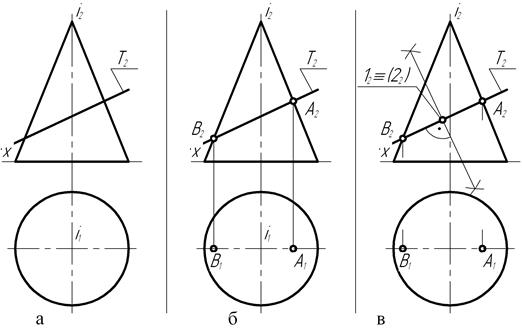
Рис. 136
Таким образом, получают на чертеже (рис. 136, и) положение проекций некоторого количества точек кривой пересечения.
Соединив затем (рис. 136, к) плавной кривой линией горизонтальные проекции точек, получают горизонтальную проекцию кривой пересечения, представляющую собой искажённую проекцию эллипса. Совмещением секущей плоскости Т (тау) с горизонтальной плоскостью проекций способом вращения получают натуральный вид эллипса – кривой пересечения прямого конуса вращения с плоскостью, пересекающей его поверхность под некоторым углом к оси вращения.
На чертеже (рис. 137) сферическая поверхность пересекается с горизонтальной плоскостью q (тэта). В сечении образуется окружность. Так как ось вращения сферы перпендикулярна горизонтальной плоскости проекций, то на чертеже фронтальный след q2 секущей плоскости располагается перпендикулярно проекции i2 оси вращения. Отрезок следа q2 секущей плоскости, находящийся внутри главного меридиана сферы, представляет собой фронтальную проекцию окружности пересечения. Причём длина этого отрезка соответствует натуральной величине диаметра окружности – кривой пересечения.
Отметив точку 12 пересечения следа q2 с главным меридианом и построив горизонтальную 11 проекцию точки на следе главной меридиональной плоскости, раствором циркуля, равным отрезку 11–i1, проводят окружность, представляющую собой горизонтальную проекцию линии пересечения сферы горизонтальной секущей плоскостью.
В случае расположения секущей плоскости (рис. 138) под углом к одной из плоскостей проекции, кривая пересечения – окружность проецируется в искаженном виде и представляет собой эллипс.
На представленном чертеже сфера пересекается фронтально-проецирующей плоскостью å (сигма), наклонённой под некоторым углом к горизонтальной плоскости проекций. Фронтальная проекция окружности сечения ограничена отрезком А2-В2 следа å2 секущей плоскости. Горизонтальная проекция окружности сечения, естественно, будет представлять собой эллипс, построение которого производят по точкам.
Среди них выделяют прежде всего точки, ограничивающие большую и малую оси эллипса. При заданном на чертеже расположении геометрических фигур: сферы и секущей плоскости, относительно плоскостей проекций, положение горизонтальной А1-В1 проекции большой оси эллипса совпадает со следом главной меридиональной плоскости.
Деление отрезка А2-В2 пополам позволяет выявить положение фронтальных проекций точек С2 и Д2, ограничивающих малую ось эллипса. Положение горизонтальных С1 и Д1 проекций точек определяют с помощью параллели сферической поверхности.
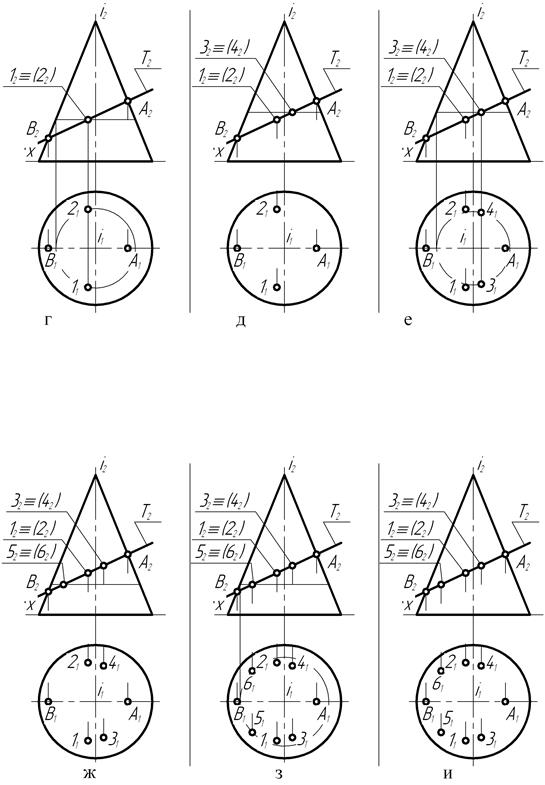
Рис. 136
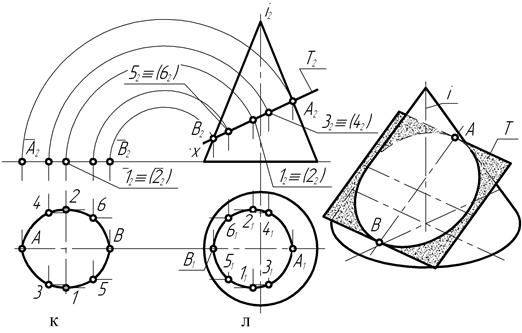
Рис. 136
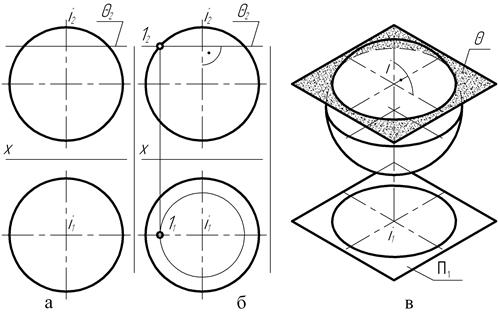
Рис. 137
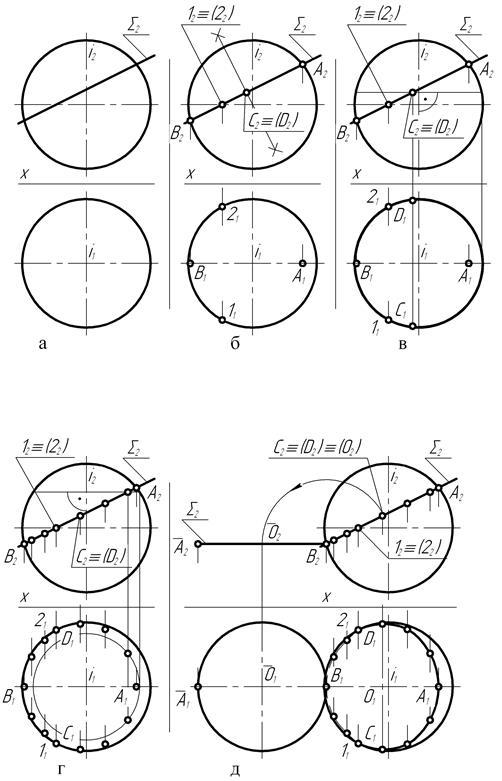
Рис. 138
В пересечении следа å2 секущей плоскости с экватором сферы выделяют положения фронтальных проекций точек 12 и 22, являющихся точками видимости проекции кривой пересечения относительно горизонтальной плоскости проекций. Горизонтальные 11 и 21 проекции этих точек располагаются на горизонтальной проекции экватора сферы.
Остальные точки кривой пересечения (рис. 138, г) являются произвольными. Выделив их положения на фронтальной плоскости проекций, с помощью параллелей строят горизонтальные проекции некоторого количества произвольных точек. И, наконец, (рис. 138, д), соединив горизонтальные проекции точек плавной кривой линией, получают горизонтальную проекцию кривой пересечения в виде эллипса.
Для построения натурального вида сечения сферы фронтально-проецирующей плоскостью å (сигма) последнюю поворачивают в положение, при котором она оказывается параллельной горизонтальной плоскости проекций.
При таком положении секущей плоскости кривая пересечения – окружность – проецируется на горизонтальную плоскость проекции в натуральную величину.
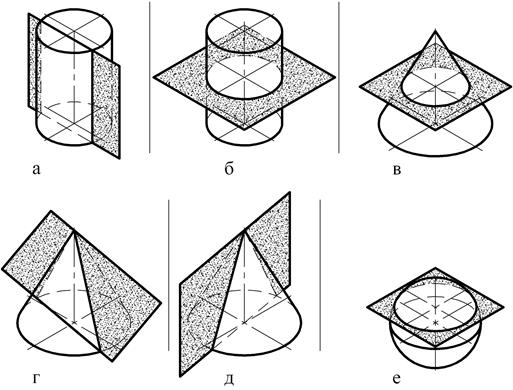
Рис. 139
Таким образом, рассмотренные примеры построения проекций линий пересечения поверхностей вращения с плоскостями частного положения – проецирующими или плоскостями уровня, свидетельствуют о том, что, во-первых, при частных положениях секущих плоскостей значительно сокращается трудоёмкость графических построений, и,
во-вторых, что для построения проекций произвольных точек кривой пересечения в большинстве случаев достаточно воспользоваться одним из приёмов, например, свойством параллелей поверхностей вращения, а для нахождения положений на чертеже проекций опорных точек приходится в каждом конкретном случае использовать свои, особые приёмы.
В заключение обратим внимание на тот факт (рис. 139), что при пересечении некоторых поверхностей вращения плоскостью в сечении образуются графически простые линии: прямые или окружности.
Отметим эти поверхности вращения и положения секущих плоскостей. Цилиндрическая поверхность пересекается по графически простым линиям в случае, если секущая плоскость располагается параллельно или перпендикулярно оси вращения.
Коническая поверхность – если секущая плоскость располагается перпендикулярно оси вращения или проходит через вершину конуса.
Сферическая поверхность в любом случае пересекается с плоскостью только по окружности.
Кроме того, при пересечении любой поверхности вращения с плоскостью, расположенной перпендикулярно оси вращения, в сечении образуется окружность – параллель поверхности вращения.
Вопросы для самопроверки
1. Какая линия получается в общем случае или пересечении поверхности вращения плоскостью?
2. С каких точек начинают построение кривой пересечения?
3. Какие точки кривой пересечения называются опорными?
4. Что такое точки видимости?
5. Какой способ в общем случае используется для определения положений на чертеже произвольных точек кривой пересечения? В чем состоит его сущность?
6. Каким условием определяется выбор вида и положения на чертеже
вспомогательной секущей плоскости для построения проекций произвольных точек кривой пересечения?
7. Каким образом можно значительно сократить трудоёмкость графических построений проекций кривой пересечения поверхностей вращения с плоскостью общего положения?
8. Какой вид имеет сечение прямого цилиндра вращения в случае пересечения его плоскостью, перпендикулярной оси вращения?
9. Какой вид имеет сечение прямого цилиндра вращения в случае пересечения его плоскостью, параллельной оси вращения?
10. Какой вид имеет сечение прямого цилиндра вращения в случае пересечения его плоскостью, не параллельной и на перпендикулярной оси вращения?
11. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, перпендикулярной оси вращения?
12. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, параллельной оси вращения?
13. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, параллельной образующей?
14. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, не перпендикулярной оси вращения и не параллельной образующей?
15. Какой вид имеет сечение прямого конуса вращения в случае пересечения его плоскостью, проходящей через вершину?
16. Какой вид имеет сечение сферы плоскостью?
17. Какие графические линии относятся к числу простых?
18. Назовите положения секущей плоскости, при которых прямой цилиндр вращения пересекается по простым графическим линиям?
19. Назовите положения секущей плоскости, при которых прямой конус вращения пересекается по простым графическим линиям?
20. При каком положении секущей плоскости сферическая поверхность пересекается по окружности?
Дата: 2019-02-25, просмотров: 339.
