Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Нормой порядка p одномерного массива [u] длины n называется число, определяемое формулой

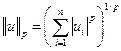.                                                       (3)

При p=1 норму называют линейной, при p=2 – квадратичной (евклидовой, а в случае комплексного массива – эрмитовой). При p=¥ формула (3) принимает вид

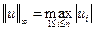.                                                                (4)

Норма матрицы, имеющей более одного столбца и более одной строки, определяется соотношением

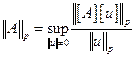.                                                 (5)

Наиболее важные свойства нормы матрицы можно выразить следующими соотношениями:

,

,

,

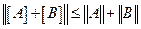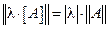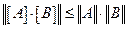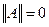 тогда и только тогда, когда ,

.

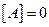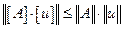В вычислительной математике обычно применяются нормы первого, второго и бесконечного порядка:

,

,

,

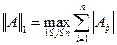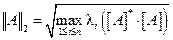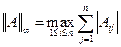где буквой l обозначены собственные значения матрицы.

Прямые методы решения СЛАУ

Наиболее часто применяемыми прямыми методами решения СЛАУ с невырожденной матрицей коэффициентов общего вида являются метод исключения Гаусса, Гауссово LU-разложение, методы диагонализации, трёхдиагонализации, вращения и т.д. Для решения СЛАУ с симметричной положительно определённой матрицей коэффициентов применяется также метод разложения Холесского (метод квадратного корня). Существуют также и другие прямые методы.

Метод исключения Гаусса основан на последовательном исключении переменных и преобразовании системы к треугольному виду. Эта часть алгоритма называется прямым ходом метода Гаусса. Следующая часть алгоритма – последовательное вычисление элементов решения, начиная с последнего и кончая первым. Эта часть называется обратным ходом. На практике в машинных расчётах чаще применяется модификация метода Гаусса, называемая методом LU-разложения.

Гауссово LU -разложение

Чтобы найти решение системы уравнений (1), матрица коэффициентов разлагается на множители:

[A] = [L]×[U],                                                   (6)

где [L] – нижняя треугольная матрица, на главной диагонали которой стоят единицы; [U] – верхняя треугольная матрица. Благодаря разложению (6) система уравнений (1) представляется в виде последовательности двух СЛАУ с треугольными матрицами коэффициентов:

[L]×[v] = [f],            [U]×[u] = [v]                           (7)

Весь алгоритм вычислений, основанный на (6), (7) можно описать следующими общими формулами:

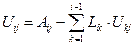, j ³ i;

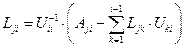, j ³ i;

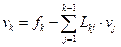, k = 1, …, n;

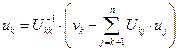, k = n, n-1, …, 1.

Разложение (6) требует примерно 2n³ арифметических операций. Вычисление решений (7) после разложения (6) требует O(n²) операций.

Алгоритм LU-разложения запишем в виде функции MATLAB.

function [L,U]=ulu(A)

n=size(A,1);

if n~=size(A,2)

L=NaN; U=NaN;

return

end

L=tril(A);

U=triu(A);

for ii=1:n

for jj=ii:n

for k=1:ii-1

U(ii,jj)=U(ii,jj)-L(ii,k)*U(k,jj);

end

for k=1:ii-1

L(jj,ii)=L(jj,ii)-L(jj,k)*U(k,ii);

end

L(jj,ii)=L(jj,ii)/U(ii,ii);

end

end

 

В представленной m-функции внутренние циклы по переменной k можно векторизовать:

function [L,U]=ulu1(A)

n=size(A,1);

if n~=size(A,2)

L=NaN; U=NaN;

return

end

L=tril(A);

U=triu(A);

for ii=1:n

for jj=ii:n

if ii>1, U(ii,jj)=U(ii,jj)-L(ii,1:ii-1)*U(1:ii-1,jj); end

if ii>1, L(jj,ii)=L(jj,ii)-L(jj,1:ii-1)*U(1:ii-1,ii); end

L(jj,ii)=L(jj,ii)/U(ii,ii);

end

end

 

Алгоритм вычисления решения треугольных СЛАУ (7) запишем в виде m-функции:

function X=uho(L,U,F)

n=size(F,1);

z=all(size(L)==n)&&all(size(U)==n)&&size(F,2)==1;

if ~z, X=NaN; return, end

v=zeros(n,1);

X=zeros(n,1);

v(1)=F(1);

for k=2:n

v(k)=F(k)-L(k,1:k-1)*v(1:k-1,1);

end

X(n)=v(n)/U(n,n);

for k=n-1:-1:1

X(k)=(v(k)-U(k,k+1:n)*X(k+1:n,1))/U(k,k);

end

Разложение Холесского

В этом методе матрица коэффициентов [A] раскладывается на треугольные множители:

[A] = [L]×[L]^T,                                                  (8)

где [L] – нижняя треугольная матрица.

Благодаря разложению (8) система уравнений (1) представляется в виде последовательности двух СЛАУ с треугольными матрицами коэффициентов:

[L]×[v] = [f],            [L]^T×[u] = [v]                           (9)

Весь алгоритм вычислений, основанный на (8), (9) можно описать следующими общими формулами:

;

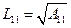L_i1 = A_i1/L₁₁ ,          i = 2, …, n;

;

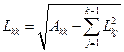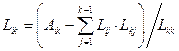,        i = k+1, …, n;

v₁ = f₁/L₁₁;

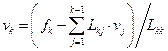, k = 2, …, n;

u_n = v_n/L_nn;

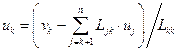, k = n–1, …, 1;

Алгоритм разложения Холесского запишем в виде m-функции:

function L=ullt(A)

n=size(A,1);

if n~=size(A,2)

L=NaN;

return

end

L(1,1)=sqrt(A(1,1));

L(2:n,1)=A(2:n,1)/L(1,1);

for k=2:n

L(k,k)=sqrt(A(k,k)-L(k,1:k-1)*L(k,1:k-1).');

L(k+1:n,k)=(A(k+1:n,k)-L(k+1:n,1:k-1)*L(k,1:k-1).')/L(k,k);

end

 

Алгоритм решения треугольных СЛАУ (9) запишем в виде m-функции:

function X=uhoh(L,F)

n=size(F,1);

z=all(size(L)==n)&&size(F,2)==1;

if ~z, X=NaN; return, end

v=zeros(n,1);

X=zeros(n,1);

v(1)=F(1)/L(1,1);

for k=2:n

v(k)=(F(k)-L(k,1:k-1)*v(1:k-1,1))/L(k,k);

end

X(n)=v(n)/L(n,n);

for k=n-1:-1:1

X(k)=(v(k)-L(k+1:n,k).'*X(k+1:n,1))/L(k,k);

end

 

Обусловленность СЛАУ

Для оценки чувствительности СЛАУ к ошибкам задания правой части и матрицы коэффициентов используется число обусловленности матрицы:

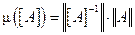.                                           (10)

Для симметричных матриц число обусловленности равно

,

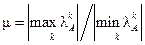где 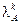 – k-e собственное значение матрицы [A].

Число обусловленности определяет, насколько погрешность входных данных может повлиять на решение системы линейных уравнений (1). Почти очевидно, что всегда m³1. Действительно,

.

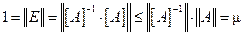При m » 1¸10 ошибки входных данных слабо сказываются на решении и система (1) считается хорошо обусловленной. При m >> 10²¸10³ система является плохо обусловленной [1].