Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n+1, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины. Требуется вычислить определённый интеграл .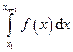

Для этого существуют различные численные методы, например, метод трапеций, метод парабол (метод Симпсона), метод интегрирования интерполирующего полинома, метод интегрирования интерполирующего сплайна и др. Применяемые в этих методах формулы называют квадратурными.

Квадратурная формула трапеций

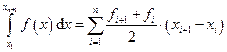.                                       (33)

Формула (33) получается в результате интегрирования кусочно-линейного интерполирующего выражения (13).

В системе MATLAB эта квадратурная формула реализуется следующей последовательностью операторов:

dx=diff(x); % Конечная разность массива аргументов

itrape=mean([y(1:end-1);y(2:end)])*dx.' % Расчётное значение интеграла

Квадратурная формула Симпсона

Пусть в точках  x₁, x₂, x₃ функция f(x) интерполирована полиномом второго порядка, т.е. параболой. Тогда

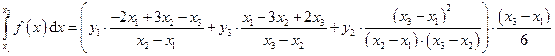. (34)

На каждой паре следующих интервалов функция f(x) также интерполирована параболами, поэтому весь интеграл равен

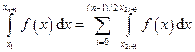                                   (35)

Соотношения (34), (35) вместе образуют квадратурную формулу Симпсона. Реализуем её в виде функции MATLAB.

% quad_simpson - численное интегрирование таблично заданной функции

% методом Симпсона (вариант для неравномерной сетки)

% integs=quad_simpson(x,y)

% Входные параметры:

% x - массив-строка значений аргумента;

% y - массив-строка значений функции.

% Выходной параметр:

% integs - определённый интеграл функции от x(1) до x(end).

function integs=quad_simpson(x,y)

dx=diff(x(1:2:end));

integs=(y(1:2:end-2)./(x(2:2:end-1)-x(1:2:end-2)).*...

(-2*x(1:2:end-2)+3*x(2:2:end-1)-x(3:2:end))+...

y(3:2:end)./(x(3:2:end)-x(2:2:end-1)).*...

(x(1:2:end-2)-3*x(2:2:end-1)+2*x(3:2:end))+...

y(2:2:end-1).*dx.^2./(x(2:2:end-1)-x(1:2:end-2))./...

(x(3:2:end)-x(2:2:end-1)))*dx.'/6;

Интегрирование методом полиномиальной интерполяции

Сначала вычисляются коэффициенты интерполирующего полинома:

a=polyapprox1(x,y,N);

Здесь N – число интервалов сетки.

Затем вычисляются коэффициенты полинома, равного первообразной интерполирующего многочлена:

ai=polyint(fliplr(a.')); % Аналитический интеграл интерполирующего полинома

ipolyn=diff(polyval(ai,[x(1) x(end)]))

В командное окно будет выдано значение интеграла.

Интегрирование методом кусочно-квадратичной интерполяции с непрерывной первой производной

c=interp_pv2(x,y);

iqadra=diff(interp_pv2_int(c,x,x([1,end])))

Здесь функция interp_pv2_int вычисляет первообразную интерполирующего сплайна в заданных точках. Разность первообразных в конце и начале интервала равна искомому интегралу. Приведём текст этой m-функции.

% interp_pv2_int - вычисление первообразной интерполяционного выражения,

% определённого в interp_pv2

% yi=interp_pv2_int(c,x,xi)

% Входные параметры:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+sum(c(4:end).*(xk-x(2:end-1)).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+c(4:end)*((xk-x(2:end-1)).*abs(xk-x(2:end-1))).'

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

% x - одномерный строчный массив исходных значений аргумента;

% xi - одномерный строчный массив аргументов вычисляемой функции;

% Выходной параметр:

% yi - одномерный строчный массив значений вычисляемой функции.

function yi=interp_pv2_int(c,x,xi)

n1=length(x)-2;

n2=length(xi);

yi=c(1)*xi+0.5*c(2)*xi.^2+c(3)*xi.^3/3+c(4:end)...

*((repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2)).^2.*...

abs(repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2)))/3;

Основы матричных вычислений