Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n+1, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины. Тогда интерполяционный полином может быть записан с использованием разделённых разностей:

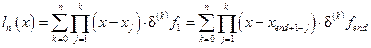.                    (27)

Полином (27) называют интерполяционным многочленом Ньютона. Он совпадает с интерполяционным полиномом Лагранжа. Остаточные члены этих полиномов также равны.

У интерполяционного многочлена Лагранжа (7) видна явная его зависимость от каждого значения функции f_i, i = 1, …, n+1. Однако при изменении n интерполяционный многочлен требуется строить заново. В этом и состоит его недостаток.

Интерполяционный многочлен Ньютона (27) выражается не через значения функции f, а через её разделённые разности. При изменении степени n у интерполяционного многочлена Ньютона требуется только добавить или отбросить соответствующее число стандартных слагаемых. Это удобно на практике.

Численное дифференцирование

Простейшими формулами расчёта производной k-го порядка таблично заданной функции являются (21) и (26). (21) применяется, если функция задана на равномерной сетке, а (26), если на неравномерной. Если бы можно было знать точку h, к которой нужно приписывать рассчитанное значение производной, то формулы (21) и (26) были бы точными. Простейшие схемы численного дифференцирования, основанные на (21) и (26), отличаются друг от друга правилами задания точки h. Такой точкой может быть один из узлов  x_i, … x_i+k  из отрезка [a, b] либо середина этого отрезка. В последнем случае оценка погрешности формул (21) и (26) при отсутствии дополнительной информации является минимальной.

Для нахождения производных любого порядка существуют формулы численного дифференцирования любого порядка точности. Один из универсальных способов численного дифференцирования состоит в том, что по значениям функции f в некоторых узлах x₁, x₂, … x_n, x_n+1 строят интерполяционный многочлен Лагранжа или Ньютона по формулам (7), (8) или (27) и приближённо полагают

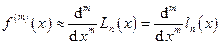.                                 (28)

Возможно также построение интерполяционных полиномов не на всех n+1 узлах, а только на k+1 узлах x_i, … x_i+k, тогда

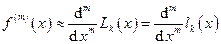.                                 (29)

Формулы (21) и (26) являются частным случаем формулы (29) при m=k.

Для разных схем численного дифференцирования существуют формулы оценки погрешности. Эти формулы не учитывают погрешности округления при вычислениях, если машинное представление чисел имеет конечную длину. Уменьшение шага сетки приводит к уменьшению систематической части погрешности и к увеличению погрешности округления, в результате чего общая погрешность будет иметь минимум при некотором значении шага сетки. Такой шаг называют оптимальным. Для разных схем численного дифференцирования существуют формулы определения оптимального шага в зависимости от машинного эпсилона.

В системе MATLAB машинным эпсилоном называют минимальное положительное число, для которого в заданном формате машинного представления чисел выполняется соотношение

1+eps > 1,                                            (30)

где eps – машинный эпсилон, однозначно определяемый длиной кода мантиссы числа с плавающей точкой.

Сплайны

Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n+1, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины.

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всём заданном отрезке [x₁, x_n+1], а на каждом частичном отрезке [x_i, x_i+1] в отдельности является некоторым алгебраическим многочленом.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [x₁, x_n+1] производной – дефектом сплайна.

Например, непрерывная кусочно-линейная функция является сплайном первой степени с дефектом, равным единице, т.к. непрерывна только сама функция (нулевая производная), а первая производная уже разрывна.

На практике наиболее широкое распространение получили сплайны третьей степени, имеющие на [x₁, x_n+1] непрерывную, по крайней мере, первую производную. Эти сплайны называются кубическими и обозначаются S₃(x). Величина m_i = S₃’(x_i) называется наклоном сплайна в точке (узле) x_i. Непрерывность производных сплайна определяется алгоритмом вычисления наклонов сплайна. Алгоритмы построения кубических сплайнов с различным значением дефекта описаны в многочисленной литературе по вычислительной математике. Они реализованы в математическом ПО, в т.ч. и в MATLAB, и в COMSOL Multiphysics.

Рассмотрим алгоритм построения сплайна второй степени S₂(x) с непрерывной первой производной. Для исключения логических операций определения принадлежности расчётной точки какому-либо интервалу сетки в качестве интерполяционного выражения примем первообразную функции (13):

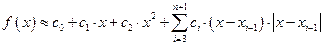,                               (31)

где ;                  ;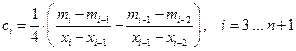

.

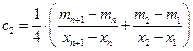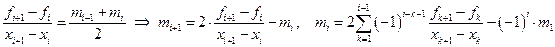Наклон сплайна в первой точке сетки определяется из условия минимальной раскачки

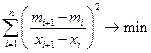, т.е. ,

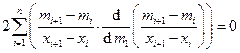откуда ;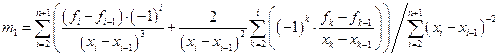

.

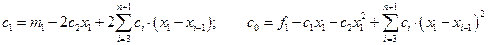Алгоритм построения сплайна S₂(x) покажем на примере m-функции в системе MATLAB.

 

% interp_pv2 - кусочно-квадратичная интерполяция таблично-заданной функции

% с непрерывной первой производной

% c=interp_pv2(x,y)

% Входные параметры:

% x - одномерный строчный массив значений аргумента интерполируемой функции;

% y - одномерный строчный массив значений функции в узлах x.

% Элементы массива x должны располагаться в порядке возрастания.

% Выходной параметр:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+sum(c(4:end).*(xk-x(2:end-1)).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+c(4:end)*((xk-x(2:end-1)).*abs(xk-x(2:end-1))).'

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

function c=interp_pv2(x,y)

n=length(x)-1;

c=zeros(1,n+2);

my=zeros(size(x));

dx=diff(x);

dy=diff(y);

d=dy./dx;

mos=ones(size(d));

mos(2:2:end)=-1;

%my(1)=sum((2*n-5:-2:1).*mos(1:end-2).*dy(2:end-1))/(x(end-1)-x(2));

my(1)=(sum(-d.*mos./dx.^2+2*cumsum(d.*mos)./dx.^2))/sum(dx.^-2);

for k=2:length(my)

my(k)=2*d(k-1)-my(k-1);

end

dmy=diff(my)./dx;

c(4:end)=0.25*diff(dmy);

c(3)=mean(dmy([1,end]))/2;

c(2)=my(1)-2*c(3)*x(1)+2*c(4:end)*(x(1)-x(2:end-1).');

c(1)=y(1)-c(2)*x(1)-c(3)*x(1)^2+c(4:end)*(x(1)-x(2:end-1).').^2;

 

% interp_pv2_eval - вычисление интерполяционного выражения, определённого в interp_pv2

% yi=interp_pv2_eval(c,x,xi)

% Входные параметры:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+sum(c(4:end).*(xk-x(2:end-1)).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+c(4:end)*((xk-x(2:end-1)).*abs(xk-x(2:end-1))).'

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

% x - одномерный строчный массив исходных значений аргумента;

% xi - одномерный строчный массив аргументов вычисляемой функции;

% Выходной параметр:

% yi - одномерный строчный массив значений вычисляемой функции.

function yi=interp_pv2_eval(c,x,xi)

n1=length(x)-2;

n2=length(xi);

yi=c(1)+c(2)*xi+c(3)*xi.^2+c(4:end)...

*((repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2)).*...

abs(repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2)));

 

Чтобы убедиться в правильности составленных m-функций выполним следующую последовательность операторов MATLAB:

 

x=linspace(-pi,pi,61);

y=exp(cos(x.^2+0.1*exp(x)))-0.1*x.^2-0.4*x;

c=interp_pv2(x,y);

xi=linspace(x(1),x(end),2001);

yi=interp_pv2_eval(c,x,xi);

plot(x,y,'g-','linewidth',2)

hold on

plot(xi,yi,'b-','linewidth',2)

 

Чтобы оценить относительную погрешность интерполяции на сетке xi, выполним следующую последовательность операторов:

ya=exp(cos(xi.^2+0.1*exp(xi)))-0.1*xi.^2-0.4*xi;

dy=norm(ya-yi)/norm(ya)

 

Получим dy= 0.0029605, т.е. погрешность интерполяции не превышает 0.3%.

Посмотрев на фигуру MATLAB, увидим, что алгоритм построения и вычисления работает правильно. Раскачка не наблюдается даже в том случае, если сетку значений аргумента сделать случайно-неравномерной.

 

figure

x1=x;

x1(2:end-1)=x1(2:end-1)+pi/60*(rand(1,length(x)-2)-0.5);

y1=exp(cos(x1.^2+0.1*exp(x1)))-0.1*x1.^2-0.4*x1;

c1=interp_pv2(x1,y1);

xi1=linspace(x1(1),x1(end),2001);

yi1=interp_pv2_eval(c1,x1,xi);

plot(x1,y1,'g-','linewidth',2)

hold on

plot(xi1,yi1,'b-','linewidth',2)

 

Оценка относительной погрешности интерполяции:

ya1=exp(cos(xi1.^2+0.1*exp(xi1)))-0.1*xi1.^2-0.4*xi1;

dy1=norm(ya1-yi1)/norm(ya1)

 

Получим dy1= 0.0029605 (то же значение, что и в предыдущем случае).