Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n+1, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины.

Формула кусочно-линейной интерполяции имеет вид:

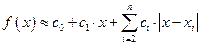,                                 (13)

где  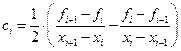 при  i = 2…n; ; .

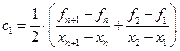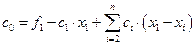Алгоритмы вычисления коэффициентов интерполяционного полинома (13), а также самого полинома при произвольных значениях аргумента оформим в виде m-функций в системе MATLAB.

% interp_pvl - кусочно-линейная интерполяция таблично-заданной функции

% c=interp_pv1(x,y)

% Входные параметры:

% x - одномерный строчный массив значений аргумента интерполируемой функции;

% y - одномерный строчный массив значений функции в узлах x.

% Элементы массива x должны располагаться в порядке возрастания.

% Выходной параметр:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+sum(c(3:end).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3:end)*abs(xk-x(2:end-1).')

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

function c=interp_pv1(x,y)

c=zeros(size(x));

d=diff(y)./diff(x);

c(3:end)=0.5*diff(d);

c(2)=mean(d([1,end]));

c(1)=y(1)-c(2)*x(1)+c(3:end)*(x(1)-x(2:end-1).');

% interp_pvl_eval - вычисление интерполяционного выражения, определённого в interp_pvl

% yi=interp_pvl_eval(c,x,xi)

% Входные параметры:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+sum(c(3:end).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3:end)*abs(xk-x(2:end-1).')

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

% x - одномерный строчный массив исходных значений аргумента;

% xi - одномерный строчный массив аргументов вычисляемой функции;

% Выходной параметр:

% yi - одномерный строчный массив значений вычисляемой функции.

function yi=interp_pvl_eval(c,x,xi)

n1=length(x)-2;

n2=length(xi);

yi=c(1)+c(2)*xi+c(3:end)...

*abs(repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2));

Как видно, формула (13) выполняет кусочно-линейную интерполяцию без использования логических выражений и позволяет создавать неразветвлённый алгоритм построения интерполяционного выражения и его вычисления.

Многочлены Чебышева

Многочленом Чебышева n-го порядка (n ³ 0) называется полином T_n(x), который на отрезке [-1, 1] задаётся формулой

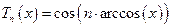.                                             (14)

В частности, полиномы Чебышева нулевого и первого порядка имеют вид

T₀(x) = 1,                                                          (15)

T₁(x) = x.                                                               (16)

Для построения полиномов Чебышева более высокого порядка можно пользоваться рекуррентным соотношением

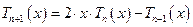.                                   (17)

Применяя рекуррентную формулу (17) к (15) и (16), получим

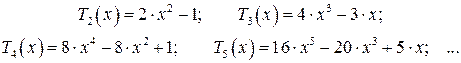
Свойства многочленов Чебышева

Свойство 1. При чётном порядке n многочлен T_n(x) содержит только чётные степени x, т.е. является чётной функцией. При нечётном порядке n многочлен T_n(x) содержит только нечётные степени x, т.е. является нечётной функцией.

Свойство 2. Старший коэффициент многочлена T_n(x) при  n ³ 1 равен 2^n-1.

Свойство 3. Многочлен T_n(x) имеет n действительных корней в интервале (-1, 1), выражаемых формулой

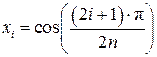,  i = 0, 1, …, n–1.

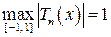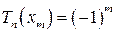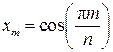Свойство 4. , причём , где , m = 0…n.

Свойство 5. Многочлен 2^1–n×T_n(x) среди всех многочленов n-й степени со старшим коэффициентом, равным единице, имеет на отрезке [-1, 1] наименьшее значение максимума модуля, т.е. не существует такого многочлена P_n(x) n-й степени со старшим коэффициентом, равным единице, что

.

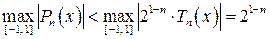Благодаря этому свойству, многочлены Чебышева  2^1–n×T_n(x)  называются многочленами, наименее уклоняющимися от нуля.

При вычислении многочлена Чебышева T_n(x) на ЭВМ по схеме Горнера при больших n происходит потеря точности из-за ошибок округления, т.к. выполняются операции вычитания близких по значению чисел. Применение формулы (17) позволяет уменьшить потерю точности.

Узлы, минимизирующие оценку погрешности
полиномиальной интерполяции

Если на отрезке [-1, 1] таблично задать функцию в точках, равных корням многочлена Чебышева T_n+1(x), т.е. в точках

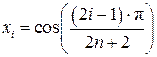,  i = 1, 2, …, n, n+1                    (18)

и интерполировать её многочленом Лагранжа L_n(x), то многочлен 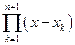  в формулах (9), (10) будет равен 2^–n×T_n+1(x), т.е. многочлену n+1 порядка, наименее уклоняющемуся от нуля. Это означает, что узлы интерполяции (18) являются оптимальными для оценки погрешности (10). Если узлы (18) линейно отобразить на отрезок [a, b], то получим оптимальные узлы интерполяции для этого отрезка:

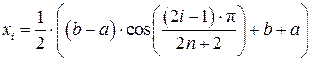, i = 1, 2, …, n, n+1.            (19)

При задании узлов интерполяции (19) оценка погрешности (10) примет вид

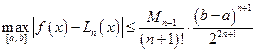,                               (20)

где .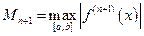

Конечные разности

Пусть дана последовательность чисел  y₁, y₂, …, y_n, y_n+1, которая может быть записана в одномерный массив y=[y₁, y₂, …, y_n, y_n+1]. Конечной разностью массива y называется массив вида Dy=[y₂–y₁, y₃–y₂, …, y_n+1–y_n]. Конечной разностью второго порядка массива y называется конечная разность массива Dy: D²y=D(Dy)=[y₃–2y₂+y₁, y₃–2y₂+y₁, …, y_n+1–2y_n+y_n-1]. Для конечных разностей высокого порядка справедливо рекуррентное соотношение

D^k y = D(D^k-1y).

Если числовая последовательность состоит из n+1 членов, то максимальный порядок конечной разности соответствующего массива равен n. Конечная разность максимального порядка может быть рассчитана по формуле

,

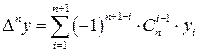где 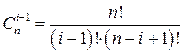 – коэффициент бинома Ньютона, который в комбинаторике называют числом сочетаний из n по i-1.

Конечные разности являются мерами изменчивости членов числовой последовательности, поэтому они могут быть использованы для приближённого расчёта производных функции, заданной числовой последовательностью на равномерной сетке значений аргумента. Пусть некоторая функция y(x) задана на сетке значений x с равномерным шагом h. Тогда если y(x)ÎC_k[x_i, x_i+k],  то существует такая точка hÎ(x_i, x_i+k), что

D^k y_i = h^k×y^(k)(h), т.е. 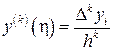,                                      (21)

где x_i+k = x_i + k×h.

Соотношение (21) можно использовать в качестве формулы приближённого численного дифференцирования таблично заданной функции на равномерной сетке.

Разделённые разности

Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n+1, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины.

Разделённой разностью первого порядка таблично заданной функции называется почленное отношение конечной разности массива значений функции к конечной разности массива аргументов функции:

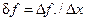.                                                  (22)

Массив значений функции  f в данном случае называется разделённой разностью нулевого порядка. Разделённая разность k-го порядка определяется через разделённую разность (k–1)-го порядка по рекуррентной формуле

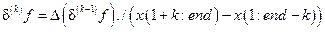.                          (23)

i-й элемент массива d^(k)f выражается через узловые значения функции по формуле

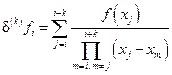.                                        (24)

Если функция f  задана на равномерной сетке значений аргумента x, т.е. x_i = x₁+(i-1)×h, то между разделённой разностью k-го порядка и конечной разностью k-го порядка имеется следующая связь:

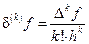.                                                 (25)

Пусть [a, b] – минимальный отрезок, содержащий узлы x_i, … x_i+k, f Î C_k[a, b],  тогда существует такая точка h Î (a, b), что

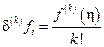, т.е. 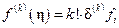.                             (26)

Соотношение (26) можно использовать в качестве формулы приближённого численного дифференцирования таблично заданной функции на произвольной сетке.