Предмет вычислительной математики. Понятие о численных и вычислительных методах

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Литература

1. Лекции по вычислительной математике: Учебное пособие / И.Б. Петров, А.И. Лобанов. – М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория знаний, 2006. – 523 с.

2. Волков Е.А. Численные методы: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1982. – 256 с.

Введение

Предмет вычислительной математики. Понятие о численных и вычислительных методах

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит главным образом не потому, что мы не умеем этого сделать, а потому что искомое решение обычно не выражается в привычных для нас элементарных или других известных функциях. Поэтому важное значение приобрели численные методы, особенно в связи с возрастанием роли математических методов в различных областях науки и техники и с появлением высокопроизводительных электронных вычислительных машин (ЭВМ) [2].

Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ. Под вычислительным методом будем понимать комбинацию численных, аналитических и алгоритмических действий для решения определённого класса задач. В зависимости от сложности задачи, заданной точности, применяемого метода и т.д. может потребоваться выполнить от нескольких десятков до многих миллиардов действий. Если число действий не превышает тысячи, то с такой задачей обычно может справиться человек, имея в своем распоряжении настольную клавишную счетную машину без программного управления и набор таблиц элементарных функций. Однако без быстродействующей ЭВМ явно не обойтись, если для решения задачи нужно выполнить порядка миллиона действий и тем более, когда решение должно быть найдено в сжатые сроки. Например, задачи, связанные с суточным прогнозом погоды, должны быть решены за несколько часов, а при управлении быстро протекающими технологическими процессами требуется находить решение за доли секунды.

Основы ручных и машинных вычислений

Цифровое представление приближённых чисел с плавающей точкой

Цифровой код приближённого числа с плавающей точкой имеет вид

a^* = ±a₀ a_-1 a_-2 … a_-m E ±b_k b_k_-1 b_k_-2 … b₁ b₀ , (21)

где a_j – цифры мантиссы; E – в этой записи условный символ, разделяющий код мантиссы и код порядка числа. Запись (21) означает, что

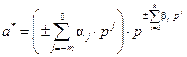. (22)

Округление чисел

При вычислениях часто возникает необходимость округления чисел, т. е. представления их с меньшим числом разрядов.

Правило округления чисел. Если в старшем из отбрасываемых разрядов стоит цифра меньше p/2, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа.

Это простое правило округления чисел применяется и в ЭВМ.

Пример. Округлить соответственно с двумя, тремя и четырьмя знаками после запятой следующие числа: 3.14159,-0.0025, 84.009974. Ответ. 3.14, -0.003, 84.0100.

Очевидно, погрешность, возникающая при округлении, не превышает по абсолютной величине половины единицы младшего оставляемого разряда.

Повторное округление не рекомендуется, так как оно может привести к увеличению погрешности. Например, если число 18.34461 сначала округлить с тремя знаками после запятой, а затем с двумя знаками, то мы последовательно получим 18,345; 18,35. При округлении сразу до двух десятичных знаков после запятой имеем 18,34. Абсолютная погрешность при повторном округлении получилась равной 0,00539, а при одноразовом округлении абсолютная погрешность имеет величину 0,00461.

При округлении приближенного числа его предельная абсолютная погрешность увеличивается с учетом погрешности округления.

Имеются следующие правила арифметических действий с приближенными числами:

При умножении и делении приближенных чисел, вообще говоря, с различным числом верных значащих цифр производится округление результата с числом значащих цифр, совпадающим с минимальным числом верных значащих цифр у исходных чисел.

При сложении и вычитании приближенных чисел, имеющих одинаковое число верных цифр после запятой, округление не производится. При сложении и вычитании приближенных чисел с различным числом верных цифр после запятой результат округляется по минимальному числу верных цифр после запятой у исходных чисел.

3амечание 1. Па практике при ручных вычислениях с целью уменьшения влияния погрешностей округления у приближенных чисел, кроме верных значащих цифр, обычно оставляют еще одну или две запасные цифры и действуют согласно сформулированным выше правилам с учетом запасных цифр. Эти запасные цифры отбрасываются при округлении окончательного результата.

Замечание 2. При вычитании близких по величине чисел может произойти значительная потеря значащих цифр и, следовательно, точности результата. Например, пусть требуется вычислить величину 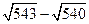, где числа 543 и 540 точные. Имеем 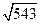= 23,30..., 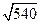= 23,23... Округлив эти числа с тремя значащими цифрами, приходим к результату только с одной значащей цифрой: .

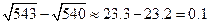Избавимся теперь от вычитания близких приближенных чисел:

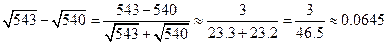
Данный результат получен при округлении частного до трёх значащих цифр, как предписывает правило умножения и деления приближённых чисел. С помощью более точных вычислений можно убедиться, что в последнем результате все три значащие цифры верные, хотя, как и в предыдущем случае, приближенные значения корне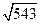й и 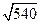использовались с тремя значащими цифрами.

Этот пример показывает, что если возможно, то следует избегать вычитания близких приближенных чисел. А если избежать этого невозможно, то следует увеличить точность промежуточных вычислений с учетом потери значащих цифр при вычитании.

Многочлены Тейлора

Пусть имеется функция 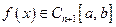. Многочленом Тейлора n-й степени функции f в точке 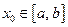называется полином

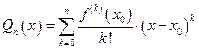. (2)

Многочлен Тейлора является приближённым представлением функции f(x) на интервале [a, b]. Этот многочлен обладает тем свойством, что в точке x=x₀ все его производные до порядка n включительно совпадают с соответствующими производными функции f, т.е.

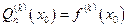, k = 0 … n

Погрешность, возникающая при замене функции f её полиномом Тейлора, выражается остаточным членом формулы Тейлора:

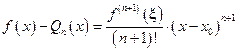, (3)

где 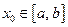, x – некоторая точка, лежащая строго между x и x₀ при x ¹ x₀. Производная 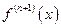по определению непрерывна на отрезке [a, b], поэтому она ограничена:

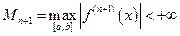. (4)

На основании (3) и (4) можно оценить погрешность аппроксимации функции f многочленом Тейлора Q_n(x):

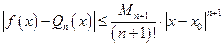, (5)

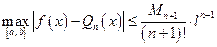, (6)

где l = max{x₀–a, b–x₀}.

Видно, что погрешность аппроксимации в окрестности точки x₀ является бесконечно малой величиной порядка n+1 порядка (O(|x–x₀|ⁿ⁺¹)). Эта погрешность быстро убывает при x®x₀.

Недостатки такой аппроксимации: существенная неравномерность погрешности на интервале [a, b] и необходимость вычисления производных высоких порядков аппроксимируемой функции. Тем не менее, многочлены Тейлора широко используются на практике для аппроксимации функций, у которых производные высоких порядков легко вычисляются, а остаточный член стремится к нулю при стремлении n к бесконечности. Большинство математических компьютерных программ использует многочлены Тейлора для вычисления элементарных функций, таких как sin, cos, exp, log и др.

Линейная интерполяция

Пусть значения некоторой функции f заданы в двух точках x₁ и x₂: f(x₁) = f₁, f(x₂) = f₂. Интерполяция такой функции по формуле (7) называется линейной, т.к. многочлен Лагранжа будет иметь первый или нулевой порядок, а это и есть линейная функция. В соответствии с (7) формула линейной интерполяции имеет вид:

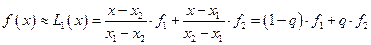. (11)

Величина 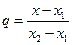называется фазой интерполяции, которая изменяется в пределах от 0 до 1 при изменении x от x₁ до x₂.

В соответствии с (10) оценка максимальной погрешности линейной интерполяции на отрезке [x₁, x₂] имеет вид

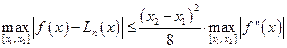. (12)

Многочлены Чебышева

Многочленом Чебышева n-го порядка (n ³ 0) называется полином T_n(x), который на отрезке [-1, 1] задаётся формулой

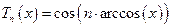. (14)

В частности, полиномы Чебышева нулевого и первого порядка имеют вид

T₀(x) = 1, (15)

T₁(x) = x. (16)

Для построения полиномов Чебышева более высокого порядка можно пользоваться рекуррентным соотношением

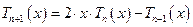. (17)

Применяя рекуррентную формулу (17) к (15) и (16), получим

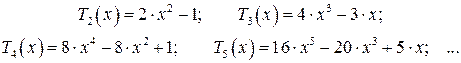
Свойства многочленов Чебышева

Свойство 1. При чётном порядке n многочлен T_n(x) содержит только чётные степени x, т.е. является чётной функцией. При нечётном порядке n многочлен T_n(x) содержит только нечётные степени x, т.е. является нечётной функцией.

Свойство 2. Старший коэффициент многочлена T_n(x) при n ³ 1 равен 2ⁿ^-1.

Свойство 3. Многочлен T_n(x) имеет n действительных корней в интервале (-1, 1), выражаемых формулой

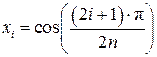, i = 0, 1, …, n–1.

Свойство 4. 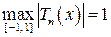, причём 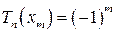, где 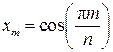, m = 0…n.

Свойство 5. Многочлен 2^1–n×T_n(x) среди всех многочленов n-й степени со старшим коэффициентом, равным единице, имеет на отрезке [-1, 1] наименьшее значение максимума модуля, т.е. не существует такого многочлена P_n(x) n-й степени со старшим коэффициентом, равным единице, что

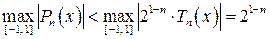Благодаря этому свойству, многочлены Чебышева 2^1–n×T_n(x) называются многочленами, наименее уклоняющимися от нуля.

При вычислении многочлена Чебышева T_n(x) на ЭВМ по схеме Горнера при больших n происходит потеря точности из-за ошибок округления, т.к. выполняются операции вычитания близких по значению чисел. Применение формулы (17) позволяет уменьшить потерю точности.

Узлы, минимизирующие оценку погрешности
полиномиальной интерполяции

Если на отрезке [-1, 1] таблично задать функцию в точках, равных корням многочлена Чебышева T_n₊₁(x), т.е. в точках

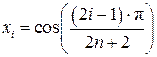, i = 1, 2, …, n, n+1 (18)

и интерполировать её многочленом Лагранжа L_n(x), то многочлен 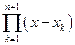в формулах (9), (10) будет равен 2^–n×T_n₊₁(x), т.е. многочлену n+1 порядка, наименее уклоняющемуся от нуля. Это означает, что узлы интерполяции (18) являются оптимальными для оценки погрешности (10). Если узлы (18) линейно отобразить на отрезок [a, b], то получим оптимальные узлы интерполяции для этого отрезка:

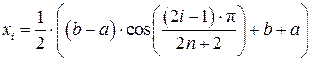, i = 1, 2, …, n, n+1. (19)

При задании узлов интерполяции (19) оценка погрешности (10) примет вид

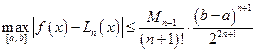, (20)

где .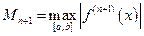

Конечные разности

Пусть дана последовательность чисел y₁, y₂, …, y_n, y_n₊₁, которая может быть записана в одномерный массив y=[y₁, y₂, …, y_n, y_n₊₁]. Конечной разностью массива y называется массив вида Dy=[y₂–y₁, y₃–y₂, …, y_n₊₁–y_n]. Конечной разностью второго порядка массива y называется конечная разность массива Dy: D²y=D(Dy)=[y₃–2y₂+y₁, y₃–2y₂+y₁, …, y_n₊₁–2y_n+y_n_-₁]. Для конечных разностей высокого порядка справедливо рекуррентное соотношение

D^k y = D(D^k^-1y).

Если числовая последовательность состоит из n+1 членов, то максимальный порядок конечной разности соответствующего массива равен n. Конечная разность максимального порядка может быть рассчитана по формуле

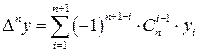где 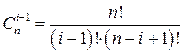– коэффициент бинома Ньютона, который в комбинаторике называют числом сочетаний из n по i-1.

Конечные разности являются мерами изменчивости членов числовой последовательности, поэтому они могут быть использованы для приближённого расчёта производных функции, заданной числовой последовательностью на равномерной сетке значений аргумента. Пусть некоторая функция y(x) задана на сетке значений x с равномерным шагом h. Тогда если y(x)ÎC_k[x_i, x_i₊_k], то существует такая точка hÎ(x_i, x_i₊_k), что

D^k y_i = h^k×y^(k)(h), т.е. 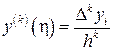, (21)

где x_i₊_k = x_i + k×h.

Соотношение (21) можно использовать в качестве формулы приближённого численного дифференцирования таблично заданной функции на равномерной сетке.

Разделённые разности

Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n₊₁, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины.

Разделённой разностью первого порядка таблично заданной функции называется почленное отношение конечной разности массива значений функции к конечной разности массива аргументов функции:

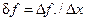. (22)

Массив значений функции f в данном случае называется разделённой разностью нулевого порядка. Разделённая разность k-го порядка определяется через разделённую разность (k–1)-го порядка по рекуррентной формуле

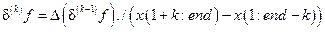. (23)

i-й элемент массива d⁽^k⁾f выражается через узловые значения функции по формуле

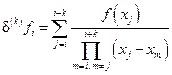. (24)

Если функция f задана на равномерной сетке значений аргумента x, т.е. x_i = x₁+(i-1)×h, то между разделённой разностью k-го порядка и конечной разностью k-го порядка имеется следующая связь:

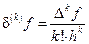. (25)

Пусть [a, b] – минимальный отрезок, содержащий узлы x_i, … x_i₊_k, f Î C_k[a, b], тогда существует такая точка h Î (a, b), что

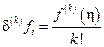, т.е. 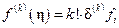. (26)

Соотношение (26) можно использовать в качестве формулы приближённого численного дифференцирования таблично заданной функции на произвольной сетке.

Численное дифференцирование

Простейшими формулами расчёта производной k-го порядка таблично заданной функции являются (21) и (26). (21) применяется, если функция задана на равномерной сетке, а (26), если на неравномерной. Если бы можно было знать точку h, к которой нужно приписывать рассчитанное значение производной, то формулы (21) и (26) были бы точными. Простейшие схемы численного дифференцирования, основанные на (21) и (26), отличаются друг от друга правилами задания точки h. Такой точкой может быть один из узлов x_i, … x_i₊_k из отрезка [a, b] либо середина этого отрезка. В последнем случае оценка погрешности формул (21) и (26) при отсутствии дополнительной информации является минимальной.

Для нахождения производных любого порядка существуют формулы численного дифференцирования любого порядка точности. Один из универсальных способов численного дифференцирования состоит в том, что по значениям функции f в некоторых узлах x₁, x₂, … x_n, x_n₊₁ строят интерполяционный многочлен Лагранжа или Ньютона по формулам (7), (8) или (27) и приближённо полагают

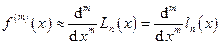. (28)

Возможно также построение интерполяционных полиномов не на всех n+1 узлах, а только на k+1 узлах x_i, … x_i₊_k, тогда

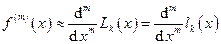. (29)

Формулы (21) и (26) являются частным случаем формулы (29) при m=k.

Для разных схем численного дифференцирования существуют формулы оценки погрешности. Эти формулы не учитывают погрешности округления при вычислениях, если машинное представление чисел имеет конечную длину. Уменьшение шага сетки приводит к уменьшению систематической части погрешности и к увеличению погрешности округления, в результате чего общая погрешность будет иметь минимум при некотором значении шага сетки. Такой шаг называют оптимальным. Для разных схем численного дифференцирования существуют формулы определения оптимального шага в зависимости от машинного эпсилона.

В системе MATLAB машинным эпсилоном называют минимальное положительное число, для которого в заданном формате машинного представления чисел выполняется соотношение

1+eps > 1, (30)

где eps – машинный эпсилон, однозначно определяемый длиной кода мантиссы числа с плавающей точкой.

Сплайны

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всём заданном отрезке [x₁, x_n₊₁], а на каждом частичном отрезке [x_i, x_i₊₁] в отдельности является некоторым алгебраическим многочленом.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [x₁, x_n₊₁] производной – дефектом сплайна.

Например, непрерывная кусочно-линейная функция является сплайном первой степени с дефектом, равным единице, т.к. непрерывна только сама функция (нулевая производная), а первая производная уже разрывна.

На практике наиболее широкое распространение получили сплайны третьей степени, имеющие на [x₁, x_n₊₁] непрерывную, по крайней мере, первую производную. Эти сплайны называются кубическими и обозначаются S₃(x). Величина m_i = S₃’(x_i) называется наклоном сплайна в точке (узле) x_i. Непрерывность производных сплайна определяется алгоритмом вычисления наклонов сплайна. Алгоритмы построения кубических сплайнов с различным значением дефекта описаны в многочисленной литературе по вычислительной математике. Они реализованы в математическом ПО, в т.ч. и в MATLAB, и в COMSOL Multiphysics.

Рассмотрим алгоритм построения сплайна второй степени S₂(x) с непрерывной первой производной. Для исключения логических операций определения принадлежности расчётной точки какому-либо интервалу сетки в качестве интерполяционного выражения примем первообразную функции (13):

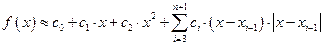, (31)

где ; ;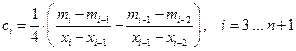

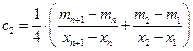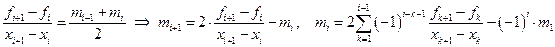Наклон сплайна в первой точке сетки определяется из условия минимальной раскачки

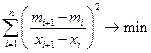, т.е. ,

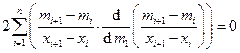откуда ;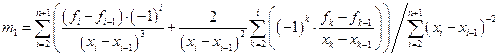

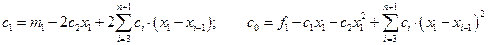Алгоритм построения сплайна S₂(x) покажем на примере m-функции в системе MATLAB.

% interp_pv2 - кусочно-квадратичная интерполяция таблично-заданной функции

% с непрерывной первой производной

% c=interp_pv2(x,y)

% Входные параметры:

% x - одномерный строчный массив значений аргумента интерполируемой функции;

% y - одномерный строчный массив значений функции в узлах x.

% Элементы массива x должны располагаться в порядке возрастания.

% Выходной параметр:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+sum(c(4:end).*(xk-x(2:end-1)).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+c(4:end)*((xk-x(2:end-1)).*abs(xk-x(2:end-1))).'

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

function c=interp_pv2(x,y)

n=length(x)-1;

c=zeros(1,n+2);

my=zeros(size(x));

dx=diff(x);

dy=diff(y);

d=dy./dx;

mos=ones(size(d));

mos(2:2:end)=-1;

%my(1)=sum((2*n-5:-2:1).*mos(1:end-2).*dy(2:end-1))/(x(end-1)-x(2));

my(1)=(sum(-d.*mos./dx.^2+2*cumsum(d.*mos)./dx.^2))/sum(dx.^-2);

for k=2:length(my)

my(k)=2*d(k-1)-my(k-1);

end

dmy=diff(my)./dx;

c(4:end)=0.25*diff(dmy);

c(3)=mean(dmy([1,end]))/2;

c(2)=my(1)-2*c(3)*x(1)+2*c(4:end)*(x(1)-x(2:end-1).');

c(1)=y(1)-c(2)*x(1)-c(3)*x(1)^2+c(4:end)*(x(1)-x(2:end-1).').^2;

% interp_pv2_eval - вычисление интерполяционного выражения, определённого в interp_pv2

% yi=interp_pv2_eval(c,x,xi)

% Входные параметры:

% с - одномерный массив параметров (коэффициентов) интерполяционной формулы

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+sum(c(4:end).*(xk-x(2:end-1)).*abs(xk-x(2:end-1)))

% y(xk)=c(1)+c(2)*xk+c(3)*xk^2+c(4:end)*((xk-x(2:end-1)).*abs(xk-x(2:end-1))).'

% Здесь интерполяционная формула записана для случая, когда xk - скаляр.

% x - одномерный строчный массив исходных значений аргумента;

% xi - одномерный строчный массив аргументов вычисляемой функции;

% Выходной параметр:

% yi - одномерный строчный массив значений вычисляемой функции.

function yi=interp_pv2_eval(c,x,xi)

n1=length(x)-2;

n2=length(xi);

yi=c(1)+c(2)*xi+c(3)*xi.^2+c(4:end)...

*((repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2)).*...

abs(repmat(xi,n1,1)-repmat(x(2:end-1).',1,n2)));

Чтобы убедиться в правильности составленных m-функций выполним следующую последовательность операторов MATLAB:

x=linspace(-pi,pi,61);

y=exp(cos(x.^2+0.1*exp(x)))-0.1*x.^2-0.4*x;

c=interp_pv2(x,y);

xi=linspace(x(1),x(end),2001);

yi=interp_pv2_eval(c,x,xi);

plot(x,y,'g-','linewidth',2)

hold on

plot(xi,yi,'b-','linewidth',2)

Чтобы оценить относительную погрешность интерполяции на сетке xi, выполним следующую последовательность операторов:

ya=exp(cos(xi.^2+0.1*exp(xi)))-0.1*xi.^2-0.4*xi;

dy=norm(ya-yi)/norm(ya)

Получим dy= 0.0029605, т.е. погрешность интерполяции не превышает 0.3%.

Посмотрев на фигуру MATLAB, увидим, что алгоритм построения и вычисления работает правильно. Раскачка не наблюдается даже в том случае, если сетку значений аргумента сделать случайно-неравномерной.

figure

x1=x;

x1(2:end-1)=x1(2:end-1)+pi/60*(rand(1,length(x)-2)-0.5);

y1=exp(cos(x1.^2+0.1*exp(x1)))-0.1*x1.^2-0.4*x1;

c1=interp_pv2(x1,y1);

xi1=linspace(x1(1),x1(end),2001);

yi1=interp_pv2_eval(c1,x1,xi);

plot(x1,y1,'g-','linewidth',2)

hold on

plot(xi1,yi1,'b-','linewidth',2)

Оценка относительной погрешности интерполяции:

ya1=exp(cos(xi1.^2+0.1*exp(xi1)))-0.1*xi1.^2-0.4*xi1;

dy1=norm(ya1-yi1)/norm(ya1)

Получим dy1= 0.0029605 (то же значение, что и в предыдущем случае).

Основы матричных вычислений

Прямые методы решения СЛАУ

Наиболее часто применяемыми прямыми методами решения СЛАУ с невырожденной матрицей коэффициентов общего вида являются метод исключения Гаусса, Гауссово LU-разложение, методы диагонализации, трёхдиагонализации, вращения и т.д. Для решения СЛАУ с симметричной положительно определённой матрицей коэффициентов применяется также метод разложения Холесского (метод квадратного корня). Существуют также и другие прямые методы.

Метод исключения Гаусса основан на последовательном исключении переменных и преобразовании системы к треугольному виду. Эта часть алгоритма называется прямым ходом метода Гаусса. Следующая часть алгоритма – последовательное вычисление элементов решения, начиная с последнего и кончая первым. Эта часть называется обратным ходом. На практике в машинных расчётах чаще применяется модификация метода Гаусса, называемая методом LU-разложения.

Гауссово LU -разложение

Чтобы найти решение системы уравнений (1), матрица коэффициентов разлагается на множители:

[A] = [L]×[U], (6)

где [L] – нижняя треугольная матрица, на главной диагонали которой стоят единицы; [U] – верхняя треугольная матрица. Благодаря разложению (6) система уравнений (1) представляется в виде последовательности двух СЛАУ с треугольными матрицами коэффициентов:

[L]×[v] = [f], [U]×[u] = [v] (7)

Весь алгоритм вычислений, основанный на (6), (7) можно описать следующими общими формулами:

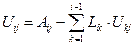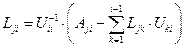, j ³ i;

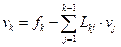, k = 1, …, n;

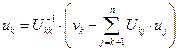, k = n, n-1, …, 1.

Разложение (6) требует примерно 2n³ арифметических операций. Вычисление решений (7) после разложения (6) требует O(n²) операций.

Алгоритм LU-разложения запишем в виде функции MATLAB.

function [L,U]=ulu(A)

n=size(A,1);

if n~=size(A,2)

L=NaN; U=NaN;

return

end

L=tril(A);

U=triu(A);

for ii=1:n

for jj=ii:n

for k=1:ii-1

U(ii,jj)=U(ii,jj)-L(ii,k)*U(k,jj);

end

for k=1:ii-1

L(jj,ii)=L(jj,ii)-L(jj,k)*U(k,ii);

end

L(jj,ii)=L(jj,ii)/U(ii,ii);

end

В представленной m-функции внутренние циклы по переменной k можно векторизовать:

function [L,U]=ulu1(A)

n=size(A,1);

if n~=size(A,2)

L=NaN; U=NaN;

return

end

L=tril(A);

U=triu(A);

for ii=1:n

for jj=ii:n

if ii>1, U(ii,jj)=U(ii,jj)-L(ii,1:ii-1)*U(1:ii-1,jj); end

if ii>1, L(jj,ii)=L(jj,ii)-L(jj,1:ii-1)*U(1:ii-1,ii); end

L(jj,ii)=L(jj,ii)/U(ii,ii);

end

Алгоритм вычисления решения треугольных СЛАУ (7) запишем в виде m-функции:

function X=uho(L,U,F)

n=size(F,1);

z=all(size(L)==n)&&all(size(U)==n)&&size(F,2)==1;

if ~z, X=NaN; return, end

v=zeros(n,1);

X=zeros(n,1);

v(1)=F(1);

for k=2:n

v(k)=F(k)-L(k,1:k-1)*v(1:k-1,1);

end

X(n)=v(n)/U(n,n);

for k=n-1:-1:1

X(k)=(v(k)-U(k,k+1:n)*X(k+1:n,1))/U(k,k);

end

Разложение Холесского

В этом методе матрица коэффициентов [A] раскладывается на треугольные множители:

[A] = [L]×[L]^T, (8)

где [L] – нижняя треугольная матрица.

Благодаря разложению (8) система уравнений (1) представляется в виде последовательности двух СЛАУ с треугольными матрицами коэффициентов:

[L]×[v] = [f], [L]^T×[u] = [v] (9)

Весь алгоритм вычислений, основанный на (8), (9) можно описать следующими общими формулами:

;

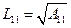L_i₁ = A_i₁/L₁₁ , i = 2, …, n;

;

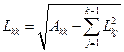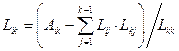, i = k+1, …, n;

v₁ = f₁/L₁₁;

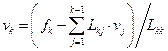, k = 2, …, n;

u_n = v_n/L_nn;

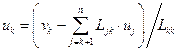, k = n–1, …, 1;

Алгоритм разложения Холесского запишем в виде m-функции:

function L=ullt(A)

n=size(A,1);

if n~=size(A,2)

L=NaN;

return

end

L(1,1)=sqrt(A(1,1));

L(2:n,1)=A(2:n,1)/L(1,1);

for k=2:n

L(k,k)=sqrt(A(k,k)-L(k,1:k-1)*L(k,1:k-1).');

L(k+1:n,k)=(A(k+1:n,k)-L(k+1:n,1:k-1)*L(k,1:k-1).')/L(k,k);

end

Алгоритм решения треугольных СЛАУ (9) запишем в виде m-функции:

function X=uhoh(L,F)

n=size(F,1);

z=all(size(L)==n)&&size(F,2)==1;

if ~z, X=NaN; return, end

v=zeros(n,1);

X=zeros(n,1);

v(1)=F(1)/L(1,1);

for k=2:n

v(k)=(F(k)-L(k,1:k-1)*v(1:k-1,1))/L(k,k);

end

X(n)=v(n)/L(n,n);

for k=n-1:-1:1

X(k)=(v(k)-L(k+1:n,k).'*X(k+1:n,1))/L(k,k);

end

Обусловленность СЛАУ

Для оценки чувствительности СЛАУ к ошибкам задания правой части и матрицы коэффициентов используется число обусловленности матрицы:

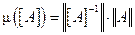. (10)

Для симметричных матриц число обусловленности равно

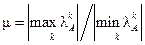где 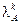– k-e собственное значение матрицы [A].

Число обусловленности определяет, насколько погрешность входных данных может повлиять на решение системы линейных уравнений (1). Почти очевидно, что всегда m³1. Действительно,

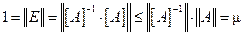При m » 1¸10 ошибки входных данных слабо сказываются на решении и система (1) считается хорошо обусловленной. При m >> 10²¸10³ система является плохо обусловленной [1].

Метод простой итерации

Если СЛАУ (1) частично разрешить относительно [u], то она примет вид

[u] = [B]×[u] + [F], (11)

где [B] = [E] – t[A], [F] = t[f], t – в общем случае произвольный скалярный множитель.

Теперь построим последовательность приближений к решению системы (11). Выберем произвольную матрицу-столбец [u₀] – начальное приближение к решению. Чаще всего его просто полагают нулевой матрицей размера (n,1). Скорее всего, начальное приближение не удовлетворяет (11), а значит, и (1). При подстановке его в исходное уравнение возникает невязка [r₀] = [f] – [A]×[u₀]. Вычислив невязку, можно уточнить приближение к решению с помощью (11), считая, что

[u₁] = [u₀] + t[r₀].

Следующие итерации будем выполнять по формулам

[r_k] = [f] – [A]×[u_k], [u_k ₊₁] = [u_k] + t[r_k]

или иначе

[u_k₊₁] = [B]×[u_k] + [F]. (12)

Итерационный метод, основанный на рекуррентной формуле (12), называется методом простых итераций.

Если предел последовательности приближений [u₀], [u₁], …, [u_k], [u_k₊₁], … существует, то говорят о сходимости итерационного процесса (12) к решению СЛАУ.

Метод простых итераций является частным случаем однослойных итерационных методов:

[u_k ₊₁] = ([E] – t_k₊₁[A])×[u_k] + t_k₊₁[f],

где t_k₊₁ – итерационный параметр, варьируемый на каждом шаге последовательных приближений.

Канонической формой записи двухслойного итерационного процесса называется следующая:

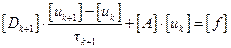При [D_k] = [E], t_k = t последняя формула соответствует однопараметрическому итерационному процессу – методу простых итераций. При [D_k] = [E], t_k = {t_k, k = 1, …, m} последняя формула соответствует m-шаговому явному итерационному процессу, при [D_k] = [D’], t_k = 1 – методу простой итерации без итерационного параметра. В случае, когда [D_k] ¹ [E], итерационный метод называется неявным, т.к. для вычисления следующего приближения к решению придётся решать систему уравнений (как правило, более простую, чем (1)).

Достаточное условие сходимости.

Итерационный процесс (12) сходится к решению СЛАУ (1) со скоростью геометрической прогрессии при выполнении условия ||B|| £ q < 1. Здесь q – основание геометрической прогрессии сходимости.

В плане численной устойчивости метод обладает таким свойством, что погрешность, вносимая в решение из-за конечной разрядности мантиссы, не зависит от количества итераций.

Литература

2. Волков Е.А. Численные методы: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1982. – 256 с.

Введение

Предмет вычислительной математики. Понятие о численных и вычислительных методах

Дата: 2019-02-25, просмотров: 203.

12 3 4 5 6 7 8 9 10 Следующая ⇒