Аппроксимацией заданной функции называется её приближённое представление функцией некоторого типового вида. При этом заданная каким-либо образом функция называется аппроксимируемой, а типовая функция называется аппроксимирующей. Параметры аппроксимирующей функции подбираются так, чтобы норма ошибки аппроксимации была минимальной. Если аппроксимируемая функция задана таблично, то минимизируется норма ошибки аппроксимации в узлах сетки. Если минимизируется L₂-норма ошибки, то говорят, что аппроксимация производится по методу наименьших квадратов. Если аппроксимирующей функцией является многочлен, то такую аппроксимацию называют полиномиальной.

Пусть известны значения некоторой функции f в n+1 различных точках x₁, x₂, … x_n, x_n+1, заданных одномерным массивом и записанных в массиве в порядке возрастания. Соответствующие значения функции f заданы одномерным массивом той же длины.

Сначала рассмотрим задачу аппроксимации таблично заданной функции полиномом нулевого порядка P₀(x) = a₀. Параметр a₀ определим методом наименьших квадратов.

.

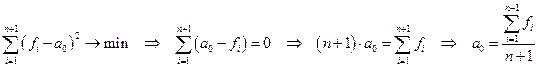Таким образом, задача аппроксимации таблично заданной функции полиномом нулевого порядка сводится к определению среднего арифметического значения функции в узлах.

Теперь в качестве аппроксимирующей функции выберем многочлен первого порядка (линейную функцию)   P₁(x) = a₀ + a₁×x.  Параметры a₀ , a₁ определим методом наименьших квадратов.

.

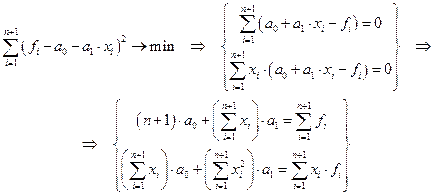Обобщим полученный результат на случай, когда в качестве аппроксимирующей функции используется многочлен P_m(x) = a₀ + a₁×x + a₂×x² + …+ a_m×x^m.  Коэффициенты аппроксимирующего полинома определяются из решения матричного уравнения

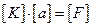,                                                     (32)

где [K] – квадратная матрица коэффициентов размера (m+1, m+1), [a] – матрица-столбец искомых коэффициентов аппроксимирующего полинома P_m(x) в порядке возрастания степеней x; [F] – матрица-столбец правой части.

,    .

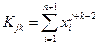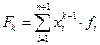Матричное уравнение (32) называют уравнением регрессии. Методы аппроксимации, основанные на составлении и решении этого уравнения, называются регрессионными.

Метод полиномиальной аппроксимации, основанный на уравнении (32), реализуем в виде функции MATLAB.

% polyapprox1 - вычисление коэффициентов полиномиальной аппроксимации

% таблично заданной функции

% a=polyapprox1(x,y,m)

% Входные параметры:

% x - массив значений аргумента таблично заданной функции;

% y - массив значений функции на сетке x;

% m - порядок аппроксимирующего полинома.

% Выходной параметр:

% a - матрица-столбец коэффициентов полинома в порядке возрастания

% степеней x.

function a=polyapprox1(x,y,m)

F=zeros(m+1,1);

K=zeros(m+1,m+1);

for jj=1:m+1

F(jj)=sum(x.^(jj-1).*y);

for k=1:m+1

   K(jj,k)=sum(x.^(jj+k-2));

end

end

a=K\F;

Для проверки выполним следующую последовательность операторов MATLAB:

x=sort(rand(1,8));

y=rand(1,8)

plot(x,y)

a=polyapprox1(x,y,7);

y1=polyval(fliplr(a.'),x)

xi=linspace(x(1),x(end),2001);

yi=polyval(fliplr(a.'),xi);

hold on

plot(xi,yi)

a3=polyapprox1(x,y,3);

y3=polyval(fliplr(a3.'),xi);

plot(xi,y3)