Если приближённое число записывается без указания его предельной абсолютной или относительной погрешности, то в мантиссе записываются только верные цифры. Верные нули на правом конце кода мантиссы отбрасывать не принято, хотя система MATLAB их отбрасывает при показе числа в командном окне.

Например, числа 0,0344 и  0,034400, как приближенные, различны. Относительно первого числа можно только утверждать, что его абсолютная погрешность не превосходит 0,0001, а из записи второго числа явствует, что его абсолютная погрешность не больше чем 10^-6.

Далее по Волкову ручная запись чисел с явным указанием предельной погрешности. Округление чисел. Правила ручных арифметических действий с приближёнными числами без явного указания предельных погрешностей. Применение запасных разрядов. Потеря значащих цифр при вычитании близких по значению чисел.

В том случае, когда у приближенного числа значащих цифр в целой части больше чем имеется верных знаков, то прибегают к записи в нормализованном виде (это и есть запись числа с плавающей точкой). Например, а^* = 3.90×10⁴. Из этой записи понятно, что у числа а^* три верные значащие цифры. В данной ситуации запись вида а^* = 39000 недопустима.

В нормализованном виде можно записать и рассмотренные выше приближенные числа: 3.44×10^-2, 3.4400×10^-2.

Часто употребляют запись вида a = a^* ± D_m(a^*) , означающую, что неизвестная величина а удовлетворяет неравенствам 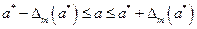. При этом величина D_m(a^*) выписывается с одной или двумя значащими цифрами, а младший разряд в а* соответствует младшему разряду в D_m(a^*). Например, а = 2,730 ± 0,017.

Записи а = 2,73018 ± 0,017, а = 2,73018 ±0,01592 неестественны.

Если по условию известно, что некоторое число точное, например, шаг вычислений h = 0,1, то верные нули справа не выписываются.

Можно говорить о числе верных значащих цифр у приближенного числа и о числе верных цифр после запятой. Как правило, при реальных вычислениях у приближенных чисел содержатся цифры после запятой, т. е. имеется дробная часть.

Например, приближенное число а^* = 25,030 имеет 5 верных значащих цифр и 3 верные цифры после запятой, а у числа b^* = 0,00404, наоборот, 3 верные значащие цифры и 5 верных цифр после запятой.

Очевидно, абсолютная погрешность приближённого числа вполне характеризуется числом верных цифр после запятой_, а относительная погрешность – числом верных значащих цифр.

Округление чисел

При вычислениях часто возникает необходимость округления чисел, т. е. представления их с меньшим числом разрядов.

Правило округления чисел. Если в старшем из отбрасываемых разрядов стоит цифра меньше p/2, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа.

Это простое правило округления чисел применяется и в ЭВМ.

Пример. Округлить соответственно с двумя, тремя и четырьмя знаками после запятой следующие числа: 3.14159,-0.0025, 84.009974. Ответ. 3.14, -0.003, 84.0100.

Очевидно, погрешность, возникающая при округлении, не превышает по абсолютной величине половины единицы младшего оставляемого разряда.

Повторное округление не рекомендуется, так как оно может привести к увеличению погрешности. Например, если число 18.34461 сначала округлить с тремя знаками после запятой, а затем с двумя знаками, то мы последовательно получим 18,345; 18,35. При округлении сразу до двух десятичных знаков после запятой имеем 18,34. Абсолютная погрешность при повторном округлении получилась равной 0,00539, а при одноразовом округлении абсолютная погрешность имеет величину 0,00461.

При округлении приближенного числа его предельная абсолютная погрешность увеличивается с учетом погрешности округления.

Имеются следующие правила арифметических действий с приближенными числами:

При умножении и делении приближенных чисел, вообще говоря, с различным числом верных значащих цифр производится округление результата с числом значащих цифр, совпадающим с минимальным числом верных значащих цифр у исходных чисел.

При сложении и вычитании приближенных чисел, имеющих одинаковое число верных цифр после запятой, округление не производится. При сложении и вычитании приближенных чисел с различным числом верных цифр после запятой результат округляется по минимальному числу верных цифр после запятой у исходных чисел.

3амечание 1. Па практике при ручных вычислениях с целью уменьшения влияния погрешностей округления у приближенных чисел, кроме верных значащих цифр, обычно оставляют еще одну или две запасные цифры и действуют согласно сформулированным выше правилам с учетом запасных цифр. Эти запасные цифры отбрасываются при округлении окончательного результата.

Замечание 2. При вычитании близких по величине чисел может произойти значительная потеря значащих цифр и, следовательно, точности результата. Например, пусть требуется вычислить величину 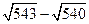, где числа 543 и 540 точные. Имеем 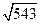= 23,30..., 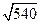= 23,23... Округлив эти числа с тремя значащими цифрами, приходим к результату только с одной значащей цифрой: .

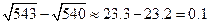Избавимся теперь от вычитания близких приближенных чисел:

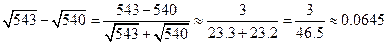
Данный результат получен при округлении частного до трёх значащих цифр, как предписывает правило умножения и деления приближённых чисел. С помощью более точных вычислений можно убедиться, что в последнем результате все три значащие цифры верные, хотя, как и в предыдущем случае, приближенные значения корней 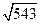 и  и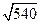спользовались с тремя значащими цифрами.

Этот пример показывает, что если возможно, то следует избегать вычитания близких приближенных чисел. А если избежать этого невозможно, то следует увеличить точность промежуточных вычислений с учетом потери значащих цифр при вычитании.