Вычисление значений многочлена. Схема Горнера

Пусть имеется алгебраический многочлен

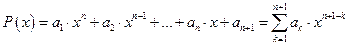,                   (1)

где a_k (k = 1…n+1) – числовые коэффициенты; n – степень многочлена. На вычислительных машинах полиномы представляются одномерными массивами коэффициентов вида [a₁ a₂ a₃ … a_n a_n+1]. Чтобы вычислить значение полинома при фиксированном x, можно поступить по-разному: сначала с помощью n-1 умножений рассчитать степени x от 2 до n, затем, выполнив n умножений и n сложений в соответствии с формулой (1), получить значение полинома P(x). Этот способ требует в общем случае при n>0 3n-1 арифметических действий.

Более экономный алгоритм вычисления значения полинома запишем на языке MATLAB и оформим его в виде m-функции:

% gorner1 - вычисление полинома скалярного аргумента методом Горнера

% Входные параметры:

% a - одномерный массив коэффициентов полинома;

% x - скалярный аргумент вычисляемой полиномиальной функции.

% Выходной параметр:

% p - скалярное значение полинома.

function p=gorner1(a,x)

n1=length(a);

p=a(1);

for k=2:n1

p=p*x+a(k);

end

Данный алгоритм называют схемой Горнера. Он требует 2n арифметических действий. В системе MATLAB этот алгоритм реализован в функции polyval. Для проверки правильности функции gorner1 в командном окне MATLAB выполним следующую последовательность операторов:

a=rand(1,5)

x=rand(1)

p1=gorner1(a,x)

p2=polyval(a,x)

p1==p2

В итоге получим ans=1. Значит, функции gorner1 и polyval возвращают одно и то же значение, т.е. в тексте функции gorner1 алгоритм закодирован правильно.

Многочлены Тейлора

Пусть имеется функция 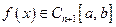. Многочленом Тейлора n-й степени функции f в точке  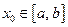называется полином

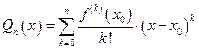.                                 (2)

Многочлен Тейлора является приближённым представлением функции f(x) на интервале [a, b]. Этот многочлен обладает тем свойством, что в точке x=x₀ все его производные до порядка n включительно совпадают с соответствующими производными функции f, т.е.

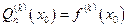, k = 0 … n

Погрешность, возникающая при замене функции f её полиномом Тейлора, выражается остаточным членом формулы Тейлора:

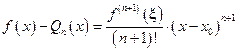,                                         (3)

где 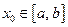, x – некоторая точка, лежащая строго между x и x₀ при x ¹ x₀. Производная  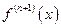по определению непрерывна на отрезке [a, b], поэтому она ограничена:

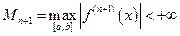.                                           (4)

На основании (3) и (4) можно оценить погрешность аппроксимации функции f многочленом Тейлора Q_n(x):

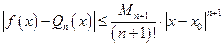,                                (5)

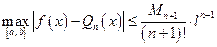,                                  (6)

где l = max{x₀–a, b–x₀}.

Видно, что погрешность аппроксимации в окрестности точки x₀ является бесконечно малой величиной порядка n+1 порядка (O(|x–x₀|ⁿ⁺¹)). Эта погрешность быстро убывает при x®x₀.

Недостатки такой аппроксимации: существенная неравномерность погрешности на интервале [a, b] и необходимость вычисления производных высоких порядков аппроксимируемой функции. Тем не менее, многочлены Тейлора широко используются на практике для аппроксимации функций, у которых производные высоких порядков легко вычисляются, а остаточный член стремится к нулю при стремлении n к бесконечности. Большинство математических компьютерных программ использует многочлены Тейлора для вычисления элементарных функций, таких как sin, cos, exp, log и др.