Введём некоторые понятия математического и функционального анализа, которые широко распространены в современной литературе по вычислительным методам [2].

1. Пусть j(h) – некоторая функция переменной h с конечной областью определения D_j на полуоси h>0, причем hÎD_j может принимать сколь угодно малые значения. Тогда, если существуют такие положительные числа h₀, c, k, что при всех hÎD_j, удовлетворяющих условию 0 < h £ h₀, выполняется неравенство

,

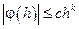то пишут

j(h) = O(h^k)

и говорят, что j(h) есть O большое от h^k (при h®0). Иначе говорят, что j(h) есть бесконечно малая величина k-го порядка (при h®0).

Согласно данному определению выполняются следующие очевидные свойства. Если j(h) = O(h^k),  y(h) = O(h^k), причем D_j = D_y,  то j(h)+y(h) = O(h^k),  т.е. O(h^k)+O(h^k) = O(h^k). Если  k>m>0, то O(h^k) в тоже время есть O(h^m). Наконец, если j(h) = O(h^k), то  аj(h) = O(h^k), где а – постоянная, не зависящая от h.

Пример. sin²(2h) = O(h²), так как  sin²(2h) £ 4h²  " h.

Пусть теперь дана функция j(h,t) положительных аргументов h, t, которые могут принимать сколь угодно малые значения. Тогда, если существуют такие положительные числа h₀, t₀, c, k, m, что при всех допустимых значениях h, t, удовлетворяющих условиям
0 < h £ h₀, 0 < t £ t₀, выполняется неравенство

,

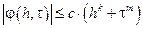то пишут

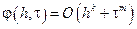
и говорят, что  j(h,t)  есть O большое от  h^k + t^m (при  h®0, t®0).

Введём еще одно аналогичное понятие.

Функция Ф(N), заданная для всех натуральных N>N₀>0, есть O большое от N^k (при N®¥), т.е.  Ф(N) = O(N^k), если найдется такая постоянная  c>0, что при всех натуральных N>N₀

|Ф(N)| £ c × N^k.

2. Будем говорить, что функция f(x) принадлежит классу C_k[a, b], и писать fÎ C_k[a, b], если функция f определена на отрезке [a, b] и имеет на нём непрерывные, производные до порядка k включительно. Это означает, что на некотором интервале (А, В), содержащем отрезок [a, b], существует k раз непрерывно дифференцируемая функция f^*, совпадающая на [a, b]  с  f.  Под значениями указанных производных функции f на концах отрезка [a, b] подразумеваются значения соответствующих производных функции f^*.

Пример.  Пусть на отрезке [0, 1] задана функция f(x) = х^5/2. Рассмотрим на интервале (-1, 2) функцию f^*(x) = |x|^5/2. Очевидно, отрезок [0, 1] содержится в интервале (-1, 2), функция f^* дважды непрерывно дифференцируема на интервале (-1, 2), а именно,

,

.

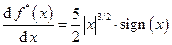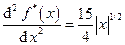Кроме того, f^*(x) = f(x) " xÎ[0, 1].  Следовательно, f Î C₂[0, 1], причём , , xÎ[0, 1].

Будем при k = 0 вместо C₀[a, b] использовать обозначение C[a, b]. Запись f Î C[a, b] означает, что функция f непрерывна на отрезке [a, b].

3. В курсе дифференциального исчисления даются понятия частных производных функции многих переменных во внутренних точках области её определения.

Для формулировок задач требуется расширить эти понятия на замкнутую область, включая граничные точки.

Пусть функция f задана на замкнутой области G  n-мерного пространства Rⁿ,  n ³ 2. Скажем, что f имеет на замкнутой области G некоторую непрерывную частную производную, если на какой-либо открытой области G^*, содержащей замкнутую область G, существует функция f^*, совпадающая с  f на G и имеющая на G^* соответствующую непрерывную частную производную. При этом в качестве значений рассматриваемой частной производной функции f в граничных точках области G примем значения соответствующей частной производной функции f^*.

Определение.  Будем говорить, что функция непрерывно дифференцируема k раз на замкнутой области G, т.е. принадлежит классу С _k(G), и писать fÎC_k(G), если функция f имеет на G все непрерывные частные производные до порядка k включительно.

Пример. Пусть на замкнутом квадрате G = {(x₁,x₂):  0 £ x_i £1, i = 1, 2} дана функция f(х₁, х₂) = x₂×cos(x₁–2)^1/2. Зададим на открытом круге  G = {(x₁,x₂): 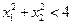} функцию f^*(х₁, х₂) по той же формуле: f^*(х₁, х₂) = x₂×cos(x₁–2)^1/2. Очевидно, G содержится в G^*, f^*(х₁, х₂) совпадает с f(х₁, х₂) на G и функция f^*(х₁, х₂) непрерывно дифференцируема k раз на G^* при любом k. Согласно данному выше определению  fÎC_k(G) " k.

4. Пусть М — множество элементов f, g, r, … произвольной природы.

Множество М  называется метрическим пространством,  если любой паре его элементов поставлено в соответствие неотрицательное число r(f, g), называемое расстоянием между элементами f и g, , которое удовлетворяет аксиомам расстояния:

1) r(f, g) = 0 тогда и только тогда, когда f = g;

2) r(f, g) = r(g, f) "(f, gÎM);

3) r(f, r) £ r(f, g) + r(g, r)  "(f, g, rÎM).

Аксиома 3 называется неравенством треугольника.

Функцию r(f, g) будем называть еще метрикой пространства М.

Примером метрического пространства служит любое множество М точек х, у, z ... n-мерного пространства Rⁿ с расстоянием

,

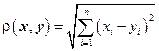где   x = (x₁, x₂, …, x_n), y = (y₁, y₂, …, y_n). Выполнение аксиом 1 и 2 для заданного расстояния очевидно, а неравенство треугольника следует из неравенства Минковского (доказываемого в курсе линейной алгебры):

|x+y| £ |x|+|y|,

где x, y – произвольные точки пространства Rⁿ, x+y=(x₁+y₁, …, x_n+y_n), 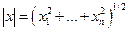. Действительно,

r(x, z) = |x–z| = |(x–y)+(y–z)| £ |x–y|+|y–z| = r(x, y)+r(y, z).

В частности, метрическим пространством с введённым выше расстоянием будет множество точек, образующих замкнутый единичный шар  S = {х: |х| £ 1}.

5. Множество М называется линейным пространством, если в нём определены операции сложения и умножения на действительные числа, не выводящие за пределы М и удовлетворяющие условиям:

1) сложение ассоциативно: (f + g) + r = f + (g + r);

2) коммутативно: f + g = g + f ;

3) существует нулевой элемент   0 Î М,  т.е.  f + 0 = f  " f Î M;

4) 0×f = 0  " f Î M;

5) (a+b)×f = af + bf ;

6) a×(f + g) = af + ag ;

7) a×(bf) = (a×b)×f ;

8) 1×f = f ;

a, b – действительные числа.

6. Система элементов  f₁, f₂, ... , f_n линейного пространства М называется линейно зависимой, если существуют такие не равные одновременно нулю числа a₁, a₂, … , a_n, что

a₁×f₁+a₂×f₂+ … +a_n×f_n = 0.

Если данное равенство возможно только при  a₁ = a₂ = … = a_n, = 0, то система элементов f₁, f₂, … , f_n, называется линейно независимой.

7. Множество  F  называется линейным нормированным пространством, если оно линейно и каждому элементу  f Î F поставлено в соответствие действительное число ||f||, называемое нормой f и удовлетворяющее аксиомам нормы:

1) ||f|| ³ 0, причём  ||f|| = 0 тогда и только тогда, когда  f = 0, т.е. f  является нулевым элементом в F;

2) ||af|| = |a|×||f||   для любого действительного a;

3) ||f+g|| £ ||f|| + ||g|| " f Î F.

Аксиома 3 называется неравенством треугольника для нормы.

Рассмотрим пример нормированного пространства. Класс C[а, b] всех непрерывных функций, заданных на отрезке [а, b], очевидно, является линейным пространством, так как сумма любых двух непрерывных функций непрерывна и непрерывная функция, умноженная на любое число, тоже непрерывна. Нулевым элементом в этом пространстве является единственная функция, тождественно равная нулю на [а, b].

Если ввести в классе C[а, b] норму

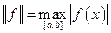,                                       (1)

то он становится нормированным пространством. Выполнение аксиом 1 и 2 для введённой нормы очевидно. Проверим неравенство треугольника. Имеем

.

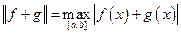Так как  |f(х) + g(х)|  является непрерывной функцией на отрезке [а, b], то по теореме Вейерштрасса найдется такая точка  x^* Î [а, b],  что

.

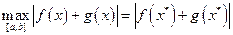Отсюда легко следует неравенство треугольника:

.

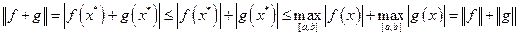8. Любое линейное нормированное пространство является одновременно метрическим пространством с расстоянием (метрикой)

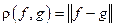.                                          (2)

Действительно, аксиомы 1 и 2 для введённого расстояния выполняются в силу аксиомы 1 и аксиомы 2 при a = -1 для нормы (см. п.4), а неравенство треугольника для расстояния (2) следует из неравенства треугольника для нормы:

.

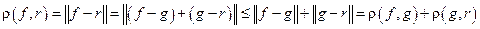9. В одном и том же линейном пространстве норму можно вводить различными способами. Например, в классе непрерывных функций С[0, 1] норму можно задать, кроме способа (1), ещё в следующем виде:

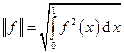.                                                         (3)

Для того чтобы различать нормы, мы будем в случае необходимости использовать индексы у нормы. Например, для нормы (1) распространены обозначения ||f||_{C[a, b]} и ||f||_C, а для нормы (3) часто используется знак ||f||_L2.

В зависимости от введенной в одном и том же линейном пространстве нормы могут изменяться различные свойства получаемого нормированного пространства и, в частности, изменяется «физический» смысл метрики, порождаемой нормой. Например, расстояние (2), заданное с помощью нормы (1), т. е.

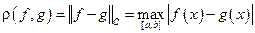,                                    (4)

означает максимальное по модулю уклонение друг от друга функций f и g на отрезке [a, b], а при использовании нормы (3) расстояние имеет вид

                         (5)

и носит смысл среднеквадратичного уклонения функций f и g.

Выбор нормы часто диктуется условиями конкретной задачи. Например, при рассмотрении равномерных приближений функций нужна норма (1), а при приближении функций методом наименьших квадратов нужна норма (3).

10. В метрическом и нормированном пространствах вводится понятие сходимости последовательности его элементов аналогично, как и в n-мерном пространстве Rⁿ.

Определение. Говорят, что последовательность {f_n} элементов метрического (нормированного) пространства сходится к его элементу f, если r(f, f_n)®0 (||f–f_n||®0) при n®¥.

Сходимость в метрическом пространстве называется сходимостью по метрике, а в нормированном пространстве – сходимостью по норме. Сходимость по метрике (4) или, что одно и то же, по норме (1) является равномерной, а сходимость по метрике (5) или по норме (3) носит название сходимости в среднеквадратичном смысле или просто сходимости в среднем.

Приближённые решения многих задач, а также их точные решения бывает удобно трактовать как элементы некоторого метрического или нормированного пространства. При этом погрешность измеряется расстоянием или нормой разности точного и приближенного решений в соответствующем пространстве.