А для коротких балок, нагруженных значительными поперечными силами вблизи опор, проводить расчет по касательным напряжениям. Для тонкостенных профилей (двутавр и швеллер) необходимо проверять прочность балки в точках, где полка сочленяется со стенкой. Здесь и нормальные, и касательные напряжения значительны.
При поперечном изгибе нормальные напряжения определяются по такой же формуле, что и при чистом изгибе.
3.40.Понятие о линейных и угловых перемещениях при изгибе. Под действием поперечных нагрузок продольная ось балки искривляется. Если материал подчиняется закону Гука, после снятия нагрузок брус выпрямляется, поэтому изогнутую ось бруса называют упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.
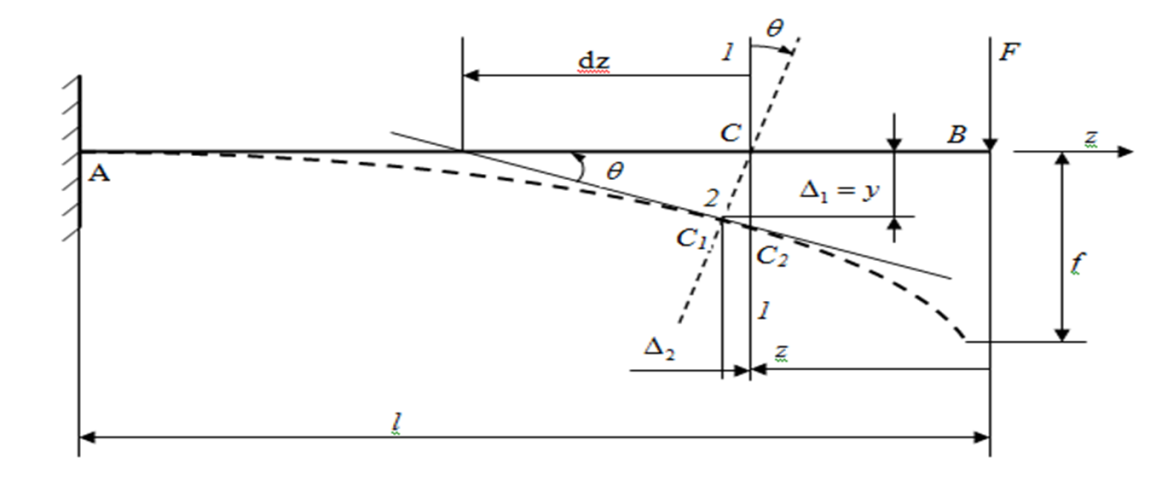
Рис.73. Линейные и угловые перемещения при поперечном изгибе
Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонтальные перемещения сечений ничтожно малы и не учитываются. Рассматривают вертикальные перемещения центра тяжести сечения, называемые прогибами (у). Максимальные прогибы обозначают: f = умаx.
Примеры расчета балок, подвергаемых изгибу.
Пример 1. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 74.
Решение. При построении эпюр для балок с одним защемленным концом можно не определять опорные реакции. Проводя сечение, будем рассматривать равновесие той части, к которой приложены только внешние (активные) силы. Для балки такой частью будет левая.
Рассматривая равновесие левой отсеченной части балки, выразим поперечную силу и изгибающий момент в произвольном сечении:
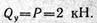
Поперечная сила положительна, так как внешняя нагрузка направлена слева от сечения вверх, Qy постоянна на всем протяжении балки.
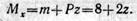
Оба слагаемых, входящих в выражение изгибающего момента, положительны, так как соответствующие внешние силы изгибают балку выпуклостью вниз.
Изгибающий момент выражается линейной функцией от абсциссы сечения z. Поэтому для построения этой эпюры достаточно найти значения изгибающего момента только в двух сечениях балки:
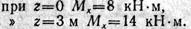
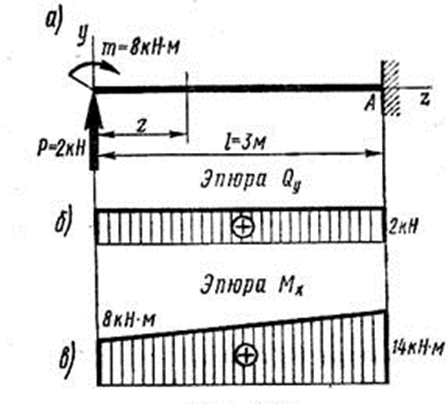
Рис.74. Расчет балки для примера 1
Пример 2. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис.75.
Решение. Определяем опорные реакции. Реакция V А направлена вверх, VB - вниз, так как эти реакции образуют пару сил, уравновешивающую пару с моментом m.
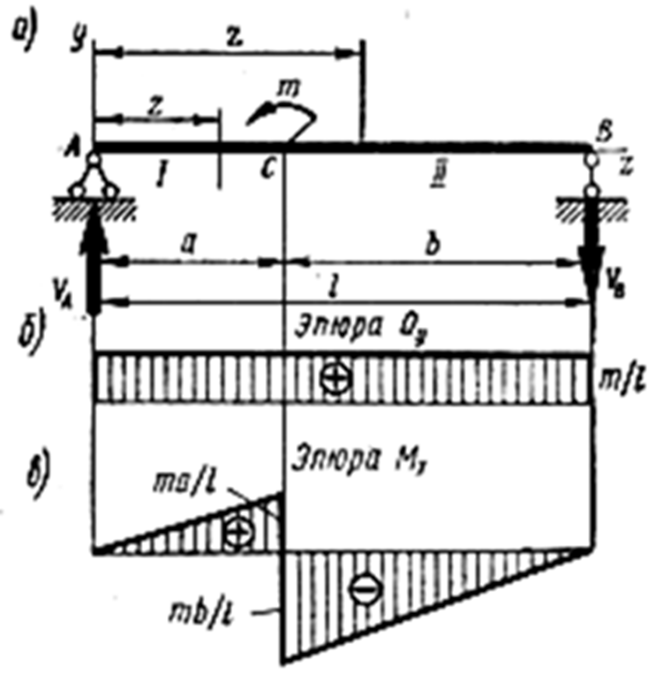
Рис.75. Расчет балки для примера 2
Составляя суммы моментов относительно опорных точек Л и В, находим:
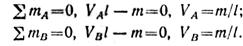
Для проверки опорных реакций составляем сумму проекций на вертикальную ось:
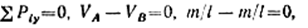
следовательно, реакции вычислены правильно.
Балка имеет два участка I, II. Проводим произвольное сечение на участке I на расстоянии z от опоры А и рассматриваем левую отсеченную часть. Поперечная сила на этом участке постоянна, равна реакции VА и положительна, так как эта реакция направлена вверх и приложена слева от сечения.
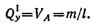
Изгибающий момент в произвольном сечении участка I:
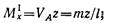
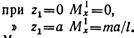
Момент положителен, так как сила VA изгибает балку выпуклостью вниз. В произвольном сечении участка II поперечная сила будет такой же, как на участке I:
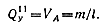
Изгибающий момент в произвольном сечении участка II:
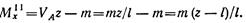
Вычислим изгибающий момент в начале и в конце участка II:

Эпюры Qy и Мх показаны на рис.75. В сечении, где приложен сосредоточенный момент, в эпюре изгибающих моментов имеется скачок, равный по величине внешнему моменту.
Пример 3. Для балки, изображенной на рис.76, построить эпюры Qy и Мx.
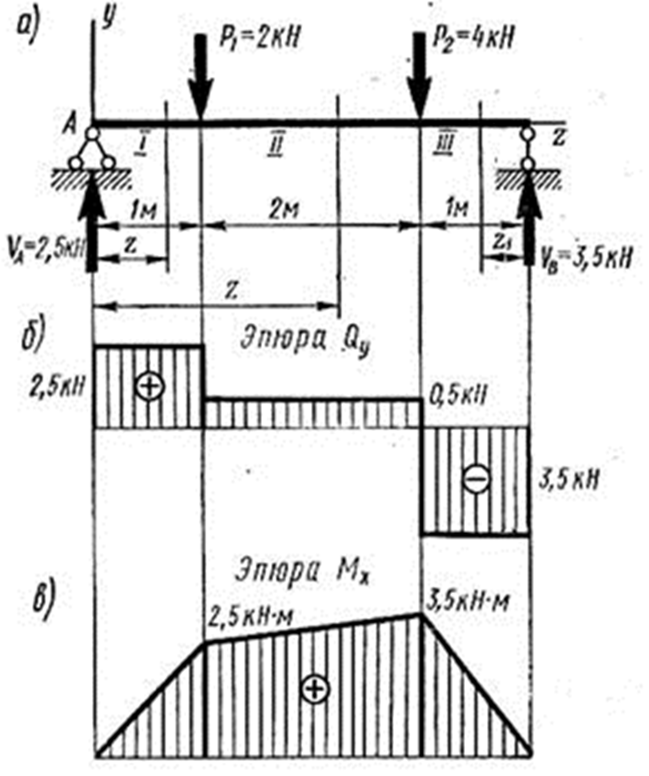
Рис.76. Расчет балки для примера 3
Решение. Определяем опорные реакции VA и VB:
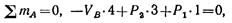
Откуда:
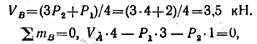
Откуда:
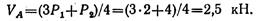
Составляем проверочное уравнение:
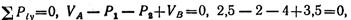
следовательно, опорные реакции определены верно.
Балка имеет три участка I, II, III: участок I — от опоры А до силы Р1 (0 < z < l м), участок II — от силы Р1 до силы Р2 (1 м << z < 3 м), участок III — от силы Р2 до опоры В. На этом участке абсциссу удобнее отсчитывать не слева, а справа, т. е. от опоры В ( 0 < z1 < 1 м).
Поперечная сила в произвольном сечении участка I:
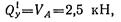
в произвольном сечении участка II:
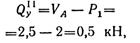
в произвольном сечении участка III:
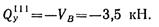
Если рассматривать левую отсеченную часть балки, то получим то же самое значение поперечной силы:
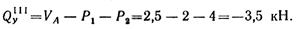
В последнем случае вычисления оказались более громоздкими, так как к левой части балки приложено три силы, а к правой — только одна. В пределах каждого участка поперечная сила постоянна. По вычисленным значениям с соблюдением правила знаков эпюра Qy построена на рис.76.
Эпюра имеет скачки под сосредоточенными силами VA, P1, Р2, VB, величина и направление скачка соответствуют величине и направлению внешней силы.
Переходим к построению эпюры изгибающих моментов. Берем сечение в пределах участка 1: слева от него расположена одна сила — опорная реакция VA. Изгибающий момент в произвольном сечении участка I:
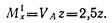
Полученное выражение является уравнением прямой, поэтому для построения эпюры моментов на этом участке достаточно найти ординаты двух точек:
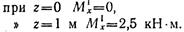
Значение ординаты Мх = 2,5 кН·м в выбранном масштабе откладываем вверх под точкой приложения силы Pv. Для определения изгибающего момента на участке II также рассматриваем равновесие левой отсеченной части балки:
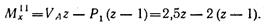
Полученное выражение является уравнением прямой. Для построения эпюры изгибающих моментов на участке II нужно определить ординаты в двух точках:
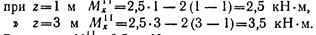
Значение MxII = 3,5 кН·м откладываем вверх под силой Р2 и соединяем с уже построенной ординатой в сечении под силой P1.
На участке III целесообразно рассмотреть правую часть балки, так как к ней приложено меньше сил, чем к левой:
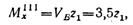
где z1 отчитывается от опоры В и изменяется в пределах от 0 до 1 м:
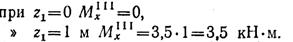
Под силой Р2 значение MxII = Mx11I, что подтверждает правильность решения. Эпюра изгибающих моментов изображена на рис.76.
3.42. Контрольная работа по дисциплине
«Сопротивление материалов».
Для выполнения контрольной работы необходимо решить свой вариант задачи.
Определить необходимое количество заклепок диаметром d для соединения внахлестку двух листов металла толщиной δ1 и δ2 под действием растягивающей силы F .
Допускаемые напряжения: [τсрез] = 150 Мпа, [σсмятие] = 280 Мпа. (Смотри табл. 9,10 и рис. 77).
Вариант исходных данных к задаче выбирается по последней и предпоследней цифре зачетной книжки.
Таблица 9.
| Вариант, последняя цифра зачетной книжки | Растягивающая сила F, кН | Диаметр заклепки d, мм |
| 0 | 100 | 2 |
| 1 | 125 | 3 |
| 2 | 150 | 4 |
| 3 | 175 | 5 |
| 4 | 200 | 6 |
| 5 | 250 | 8 |
| 6 | 300 | 10 |
| 7 | 350 | 12 |
| 8 | 400 | 16 |
| 9 | 450 | 18 |
Таблица 10.
| Вариант, предпоследняя цифра зачетной книжки | Толщина первого листа δ1, мм | Толщина второго листа δ2 , мм |
| 0 | 1 | 2 |
| 1 | 2 | 2 |
| 2 | 4 | 6 |
| 3 | 6 | 6 |
| 4 | 8 | 8 |
| 5 | 10 | 12 |
| 6 | 12 | 14 |
| 7 | 14 | 16 |
| 8 | 16 | 16 |
| 9 | 18 | 20 |
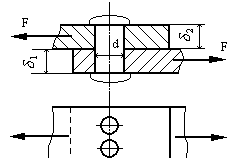
Рис.77. Соединение внахлестку двух листов металла заклепками
4.Основы дисциплины «Теория механизмов и машин».
Лекция 1. Что изучает дисциплина «Теория механизмов и машин». Звено, кинематическая пара, механизм, машина. Классификация машин и механизмов. Классификация кинематических пар, класс кинематической пары. Кинематическая цепь. Структурный анализ механизма.
Лекция 2. Цель и задачи кинематического анализа механизма. Методы кинематического анализа. Методы планов положений, скоростей и ускорений. Аналитические методы кинематического анализа механизма.
Лекция 3. Цель и задачи динамического анализа механизма. Определение сил, действующих на звенья механизма. Определение динамических нагрузок при поступательном, вращательном и плоскопараллельном движении звеньев. Графоаналитический метод кинетостатического расчета. Определение уравновешивающей силы по теореме Жуковского. Определение истинного закона движения ведущего звена механизма, диаграмма Виттенбауэра.
Контрольная работа по дисциплине «Теория механизмов и машин».
Курсовой проект (курсовая работа) по дисциплине «Теория механизмов и машин».
4.1.Что изучает дисциплина «Теория механизмов и машин». ТММ изучает: строение (структуру), кинематику и динамику механизмов при их анализе и синтезе.
Цель дисциплины ТММ - анализ и синтез типовых механизмов. Основные задачи дисциплины ТММ - разработка общих методов исследования строения (структуры), кинематики и динамики типовых механизмов.
Анализ механизма - дан механизм, требуется определить его свойства, характеристики. Синтез механизма - заданы свойства (характеристики) механизма, требуется создать механизм. Вторая задача намного сложнее первой.

Рис.78. Объект исследования дисциплины ТММ
4.2.Основные термины, понятия и определения в ТММ. Машина - это устройство, предназначенного для преобразования: энергии, материалов, информации.
В зависимости от выполняемых функций машины можно разделить на следующие классы: энергетические (двигатель внутреннего сгорания, турбины), технологические (токарный станок), транспортные (автомобили, лифты, транспортеры), кибернетические (компьютеры, искусственное сердце, почки).
Каждая машина состоит чаще всего из нескольких механизмов. Механизм - это система тел, предназначенных для преобразования одного вида движения в другой вид движения. Например: вращательное движение преобразуется во вращательное, вращательное в возвратно-поступательное и т.д.
С точки зрения функционального назначения механизмы делятся на следующие виды: механизмы двигателей (ДВС), передаточные механизмы (редуктора), исполнительные механизмы (механизмы прессов, металлорежущих станков), механизмы управления (механические щупы), механизмы транспортировки (винтовые шнеки для транспортировки сыпучих материалов), механизмы взвешивания и упаковки продукции и т.д.

Рис.79. Основные понятия в ТММ: машина, механизм, звено,
Кинематическая пара
Механизм состоит из звеньев. Стойка - неподвижное звено любого механизма. Кривошип - совершает вращательное движение (полный оборот вокруг оси). Коромысло (качающееся звено) - совершает неполный оборот вокруг оси. Шатун - совершает сложное плоско-параллельное движение (движется поступательно и одновременно вращается). Ползун - совершает возвратно-поступательное движение. Кулиса - звено, совершающее поступательное, вращательное или качательное движения, по которому перемещается ползун. В этом случае ползун называют камень кулисы.
Звенья в механизме соединяются между собой подвижным соединением. Подвижное соединение двух звеньев называется кинематической парой.
Кинематические пары
Классы Группы
Звено Звено
Подвижное соединение
Рис.80. Кинематическая пара
Если соединяются два звена, то будет одна кинематическая пара. Если соединяются три звена, то будет две кинематических пары. Если соединяются N звеньев, то будет N-1 кинематическая пара.
4.3. Классификация кинематических пар. Кинематические пары делятся на классы и группы. Класс кинематической пары определяется по числу ограничений, накладываемых на взаимное движение звеньев пары. Класс кинематической пары = S (числу ограничений).
H = 6
S = 0
H - степень свободы
S = 6 - H
S - число ограничений
Y
Рис.81. Алгоритм определение класса кинематической пары
H = 5; S = 1; класс 1.
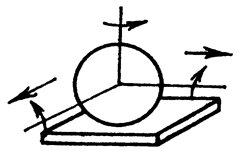
Рис.82. Кинематическая пара: шар – плоскость (высшая, 1-го класса)
H = 3; S = 3; класс 3.
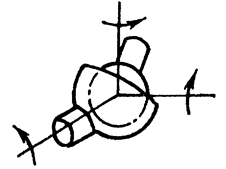
Рис.83. Сферическая кинематическая пара (низшая, 3-его класса)
H = 3; S = 3; класс 3.
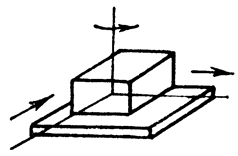
Рис.84. Плоскостная кинематическая пара (низшая, 3-его класса)
H = 2; S = 4; класс 4.

Рис.85. Цилиндрическая кинематическая пара (низшая, 4-го класса)
H = 1; S = 5; класс 5.
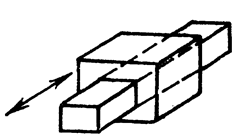
Рис.86. Поступательная кинематическая пара (низшая, 5-го класса)
H = 1; S = 5; класс 5.
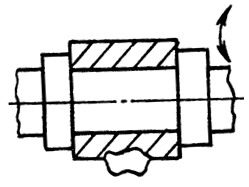
Рис.87. Вращательная кинематическая пара (низшая, 5-го класса)
H = 1; S = 5; класс 5.

Рис.88. Винтовая кинематическая пара (низшая, 5-го класса)
В винтовой кинематической паре вращение винта и его перемещение взаимосвязаны. Следовательно, степеней свободы не две, а одна. Тогда ограничений пять и класс кинематической пары пятый.
Кинематические пары делятся на группы: высшие и низшие. Высшие кинематические пары - контакт между звеньями происходит по линии или в точке. Низшие кинематические пары - контакт между звеньями происходит по поверхности.
4.4. Кинематические цепи. Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами.
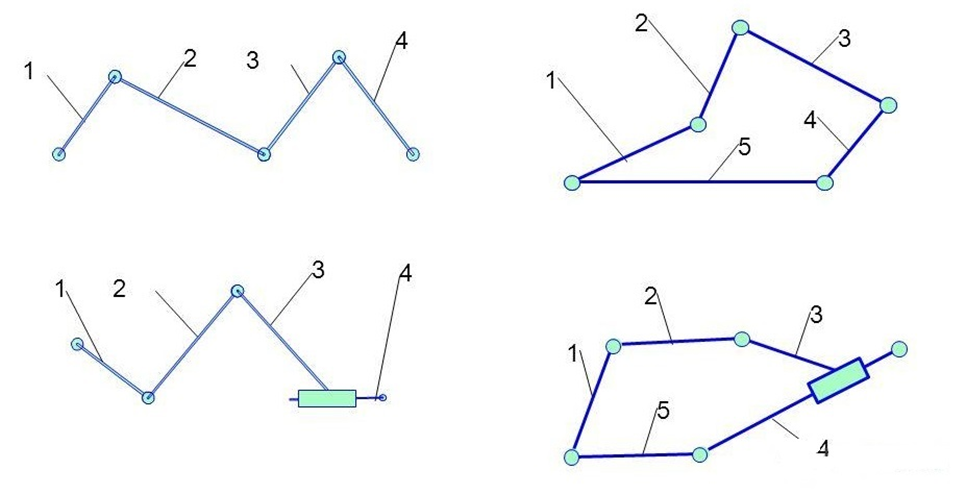
Рис.89. Кинематические цепи: разомкнутые и замкнутые
Имеется определенная классификация кинематических цепей - цепи могут быть простыми и сложными, замкнутыми (закрытыми) и разомкнутыми (открытыми), пространственными и плоскими. Любой механизм представляет из себя кинематическую цепь, в которой одно звено является неподвижным (стойка).
4.5. Степень подвижности плоских механизмов. Под степенью
подвижности понимается число степеней свободы всех подвижных звеньев механизма относительно неподвижного звена (стойки). Степень подвижности определяется по формуле Чебышева П.Л.:
W ═ 3·n ― 2·p5 ― p4 ,
где:
W – степень подвижности,
n - число подвижных звеньев механизма (кинематической цепи),
p5 - число кинематических пар пятого класса,
p4 - число кинематических пар четвертого класса.
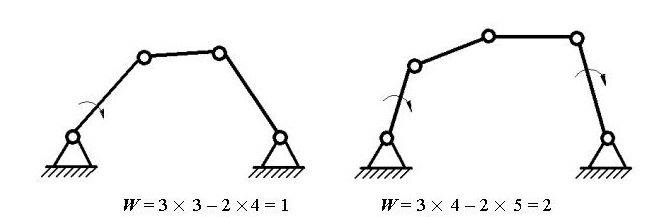
Рис.90. Определение степени подвижности плоского механизма
По формуле Чебышева П.Л.
4.6. Принцип образования плоских механизмов, предложенный
Ассуром Л.В.: «К ведущему звену и стойке последовательно присоединяются кинематические цепи с нулевой степенью подвижности». Эти цепи называются группы Ассура.
W=1 W=0 W=0 W=1
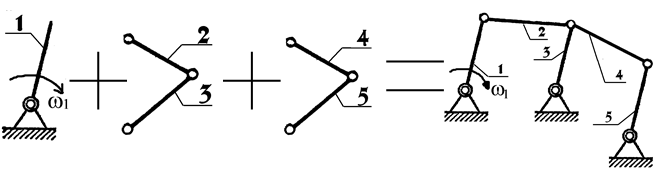
Исходный Группы Ассура
механизм 2-го класса. Новый механизм
(1-го класса). 2-го класса.
Рис.91. Принцип образования плоских механизмов
Кинематическая цепь с нулевой степенью подвижности, которая не распадается на более простые кинематические цепи, также обладающие нулевой степенью подвижности называется группой Ассура.
Группы Ассура бывают: 2-го, 3-его и 4-го классов. Порядок группы Ассура определяется числом элементов, которыми она присоединяется.
Группа Ассура 2-го класса состоит из двух звеньев, группы Асура
3-его и 4-го классов состоят из четырех звеньев.
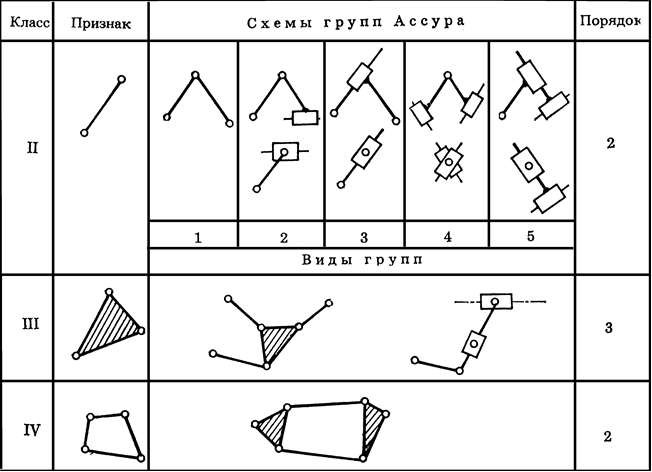
Рис.92. Классификация групп Ассура
4.6.1. Алгоритм структурного анализа механизма. Цель структурного анализа механизма - определить класс механизма. Класс механизма равен наивысшему классу группы Ассура, входящей в состав механизма.
1. Начертить структурную схему механизма.
2. Обозначит все подвижные звенья механизма.
3.Заглавными буквами латинского алфавита обозначить все кинематические пары и указать класс кинематической пары.
4. Определить степень подвижности механизма по формуле Чебышева П.Л.
5. Удалить лишние степени свободы (если они есть).
6. Удалить пассивные связи (если они есть).
7. Заменить высшие кинематические пары на низшие.
8. Отсоединить от механизма группу Ассура 2-го класса (два звена), так чтобы: оставшийся механизм продолжал работать, а степень его подвижности (W) не менялась (оставалась прежней).
9. Если нельзя отсоединить группу Ассура 2-го класса, то отсоединить группу Ассура 3-го класса (четыре звена) так, чтобы: оставшийся механизм продолжал работать, а W не менялась.
10. Если нельзя отсоединить группу Ассура 3-го класса, то отсоединить группу Ассура 4-го класса, так, чтобы: оставшийся механизм продолжал работать, а W механизма не менялась.
11. Класс механизма определяем по наивысшему классу группы Ассура, входящей в состав механизма.
4.7. Вопросы для самопроверки по структурному анализу механизма.
1. Кто из выдающихся деятелей культуры эпохи Возрождения разработал проекты конструкций механизмов ткацких станков, печатных машин ?
Ответ: Леонардо да Винчи (1452-1519).
2. Действительный член Петербургской Академии наук XVIII века, автор 850 научных трудов, в том числе: «О машинах вообще» (1753 г.) и «Принципы теории машин»?
Ответ: Леонард Эйлер (1707-1783).
3. Какой русский механик впервые разработал проект двухцилиндрового парового двигателя и осуществил в 1765 году его испытание?
Ответ: Ползунов Иван Иванович.
4. Именем какого русского ученого названа структурная формула плоских механизмов?
Ответ: Чебышев Пафнутий Львович.
5. «Отец русской авиации», который был не только основоположником современной аэродинамики, но и автор целого ряда работ по прикладной механике и теории регулирования хода машин?
Ответ: Жуковский Николай Егорович.
6. Автор учебников, академик, организатор советской школы теории механизмов и машин, зав. кафедрой ТММ в МАИ ?
Ответ: Артоболевский Иван Иванович.
7. Что такое звено механизма? Ответ: твёрдое тело, состоящее из одной или нескольких деталей.
8. Что такое анализ механизма? Ответ: исследование структурных, кинематических или динамических свойств механизма.
9. Из чего состоит механизм?
Ответ: из отдельных звеньев.
10. Как называется каждая подвижная деталь или группа деталей, образующих одну жесткую систему тел в механизме?
Ответ: подвижное звено механизма.
11. Как называются неподвижные детали, которые образуют одну жесткую неподвижную систему тел в механизме?
Ответ: неподвижное звено (стойка).
12. Сколько неподвижных звеньев в механизме?
Ответ: 1.
13. Чем отличается механизм от кинематической цепи?
Ответ: наличием стойки.
14. Как называется соединение двух соприкасающихся звеньев, допускающее их относительное движение?
Ответ: кинематическая пара.
15. Как называется система звеньев, связанных между собой кинематическими парами?
Ответ: кинематическая цепь.
16. Чему равен максимальный класс кинематической пары?
Ответ: 5.
17. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 5?
Ответ: S = 6 - H = 6 - 5 = 1
18. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 4?
Ответ: S = 2
19. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 3?
Ответ: S = 3.
20. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 1?
Ответ: S = 5.
21. Назовите максимальное число условий связи?
Ответ: S=5.
22. Назовите максимальное число степеней свободы звена кинематической пары в относительном движении?
Ответ: H = 5.
23. Чему равно число степеней свободы, если число условий связи равно 1?
Ответ: H = 5, так как H = 6 - S.
24. Чему равно число степеней свободы, если число условий связи равно 2?
Ответ: H = 4.
25. Чему равно число степеней свободы, если число условий связи равно 4?
Ответ: H = 2.
26. Чему равно число степеней свободы, если число условий связи равно 5?
Ответ: H = 1.
27. Как называется кинематическая пара, если её звенья соприкасаются по поверхности?
Ответ: низшая кинематическая пара.
28. Как называется кинематическая пара, если её звенья соприкасаются по линии или в точке?
Ответ: высшая кинематическая пара.
29. Напишите формулу Чебышева П. Л.
Ответ: W = 3n-2p5-p4.
30. Как называется кинематическая цепь, степень свободы которой равна нулю?
Ответ: ферма.
31. Как влияют лишние степени свободы на закон движения ведомого звена и однозначность его перемещения?
Ответ: никак.
32. Напишите название кинематической пары, которая представляет собой шар, перекатывающийся со скольжением по плоскости
Ответ: шар – плоскость.
33. Напишите класс кинематической пары, которая представляет собой шар, перекатывающийся со скольжением по плоскости.
Ответ: 1 класс.
34. Как называется кинематическая пара, представляющая собой цилиндр, лежащий на плоскости?
Ответ: высшая кинематическая пара 2-го класса.
35. Напишите формулу Сомова-Малышева.
Ответ: W=6n - 5p5 - 4p4 - 3p3 - 2p2 - p1.
36. Начертите условное изображение пары:
шар-плоскость.
37. Начертите условное изображение пары:
сферическая (шаровая).
38. Начертите условное изображение пары:
плоскостная.
39. Начертите условное изображение пары:
цилиндрическая.
40. Начертите условное изображение пары:
сферическая с пальцем.
41. Начертите условное изображение пары:
поступательная.
42. Начертите условное изображение пары:
вращательная.
43. Начертите условное изображение пары:
винтовая.
44. Как классифицируют кинематические пары?
Ответ: по числу S (условий связи). S = 6 – H.
45. Название пары, допускающей относительное вращательное движение звеньев вокруг оси?
Ответ: вращательная пара.
46. Название пары, допускающей лишь прямолинейное поступательное относительное движение звеньев?
Ответ: поступательная пара.
47. Название пары., допускающей независимые вращательное и поступательное относительные движения звеньев?
Ответ: цилиндрическая пара.
48. Название пары, допускающей три независимых относительных вращения звеньев, вокруг осей x, y, z.
Ответ: сферическая пара.
49. Как называется механизм, все подвижные звенья которого движутся в параллельных плоскостях?
Ответ: плоский механизм.
50. Как называется механизм, подвижные звенья которого описывают траектории, лежащие в пересекающихся плоскостях?
Ответ: пространственный механизм.
51. Что произойдет, если S=6?
Ответ: кинематическая пара становится жестким соединением деталей, т.е. одним звеном.
52. Что произойдет, если S=0?
Ответ: пары не существует, а имеются 2 тела, движущихся независимо друг от друга.
53. Что представляет собой механизм 1-го класса?
Ответ: это механизм, состоящий из подвижного звена и стойки.
54. Чему равно число механизмов 1-го класса в механизме?
Ответ: число механизмов 1-го класса равно числу степеней свободы механизма.
55. Как называется звено, совершающее полный оборот вокруг неподвижной оси?
Ответ: кривошип.
56. Как называется подвижное звено (вращающееся, качающееся или движущееся возвратно-поступательно), которое является направляющей ползуна?
Ответ: кулиса.
57. Что такое группа Ассура?
Ответ: это кинематическая цепь с нулевой степенью подвижности, которая не распадается на более простые кинематические цепи, также обладающие нулевой степенью подвижности.
58. Какое число звеньев должно быть в группе Ассура?
Ответ: чётное (2 или 4).
59. На что подразделяются группы Ассура?
Ответ: на классы, порядки и виды
60. Чем определяется порядок групп Ассура?
Ответ: числом элементов, которыми она присоединяется.
61. В каком году Ассур Л.В. сформулировал принцип образования плоских механизмов?
Ответ: 1914г.
62. Для каких механизмов подходит формула Чебышева для подсчёта степени подвижности?
Ответ: для плоских.
63. Что можно определить при помощи следующей формулы:
W = 3n – 2p5 – р4?
Ответ: степень подвижности плоского механизма.
64. В каких механизмах все звенья перемещаются в одной или параллельных плоскостях?
Ответ: в плоских.
65. В каких механизмах звенья перемещаются в пересекающихся плоскостях?
Ответ: в пространственных.
66. Что в формуле Чебышева обозначается как р4?
Ответ: число кинематических пар 4-го класса.
67. Что в формуле Чебышева обозначается как р5?
Ответ: число кинематических пар 5-го класса.
68. Что определяет формула Сомова-Малышева?
Ответ: степень подвижности пространственного механизма.
69. Как определить число кинематических пар в сложном шарнире?
Ответ: подсчитать число соединяемых звеньев (подвижных и неподвижных) и вычесть единицу.
70. Что изучает ТММ?
Ответ: строение, кинематику и динамику машин и механизмов при их анализе и синтезе.
71. Что такое машина?
Ответ: устройство для преобразования энергии, информации и материала.
72. Что такое механизм?
Ответ: система звеньев, которая предназначена для преобразования одного движения в другое.
73. Какое звено называется шатун?
Ответ: звено, совершающее сложное плоско параллельное движение.
74. Какое звено называется ползун?
Ответ: звено, совершающее поступательное прямолинейное движение.
75. Какое звено называется коромысло?
Ответ: звено, которое совершает неполный оборот вокруг оси, связанной со стойкой.
76. Чем отличается звено механизма от детали механизма?
Ответ: звено механизма состоит из одной или нескольких деталей.
77. Какое звено называется стойкой?
Ответ: неподвижные детали, которые образуют одну жесткую неподвижную систему тел в механизме.
78. Что такое кинематическая цепь?
Ответ: система звеньев, связанных между собой кинематическими парами.
79. Что такое кинематическая пара?
Ответ: подвижное соединение двух соприкасающихся звеньев.
80. Сколько классов кинематических пар Вы знаете?
Ответ: пять классов.
81. Напишите алгоритм определения класса кинематической пары.
Ответ: подсчитать число простейших движений, которыми обладает звено кинематической пары в относительном движении; вычесть полученное число из шести, получив при этом число связей, налагаемых данной кинематической парой на относительное движение её звеньев, и этим определим класс пары.
82. Определите класс кинематической пары, образованной звеньями: шар – плоскость.
Ответ: S = 6 – H = 6 – 5 = 1, 1 класс.
83. Определите класс кинематической пары, образованной звеньями: плоскость – цилиндр.
Ответ: S = 6 – H = 6 – 4 = 2, 2 класс.
84. Алгоритм замены высшей кинематической пары на низшую.
Ответ: проводим нормаль через точку касания кривых и отмечаем на ней центры кривизны кривых, образующих вращательные пары, в которых соединяются условные звенья.
85. С какой целью удаляют из механизма пассивные связи?
Ответ: чтобы упростить механизм, так как пассивные связи не оказывают никакого влияния на характер движения механизма.
86. С какой целью удаляют из механизма лишние степени свободы?
Ответ: чтобы упростить механизм.
87. С какой целью конструктора применяют в механизмах пассивные связи?
Ответ: для повышения его жесткости или для устранения неопределенности движения звеньев в некоторых положениях.
88. С какой целью конструктора применяют в механизмах лишние степени свободы?
Ответ: для уменьшения сил трения и износа звеньев.
89. Принцип образования плоских механизмов.
Ответ: последовательное присоединение кинематических цепей, являющимися группами Ассура.
90. Что такое механизм первого класса?
Ответ: это механизм с одной степенью свободы, состоящий из стойки и подвижного звена.
91. Алгоритм структурного анализа механизма.
Ответ: Построить кинематическую схему механизма. Обозначить все подвижные звенья механизма. Заглавными буквами латинского алфавита обозначить все кинематические пары и класс кинематической пары. Удалить лишние степени свободы (если они есть). Удалить пассивные связи (если они есть). Определить степень подвижности механизма. Заменить высшие кинематические пары на низшие. Отсоединить от механизма группу Ассура 2-го класса (два звена) так, чтобы: оставшейся механизм продолжал работать, а W не менялась. Если нельзя отсоединить группу Ассура 2-го класса, то отсоединить группу Ассура 3-го класса (четыре звена) так, чтобы: оставшейся механизм продолжал работать, а W не менялась. Если нельзя отсоединить группу Ассура 3-го класса, то отсоединить группу Ассура 4-го класса, так, чтобы: оставшейся механизм продолжал работать, а W механизма не менялась.
92. Цель структурного анализа механизма.
Ответ: определить класс механизма.
93. Алгоритм определения степени подвижности плоского механизма по формуле Чебышева.
Ответ: определить число подвижных звеньев, определить число кинематических пар, определить среди них высшие и низшие, посчитать по формуле Чебышева степень подвижности.
94. Начертите группу Ассура 4го класса.
Ответ: 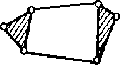
95. Начертите группу Ассура 3го класса.
Ответ:
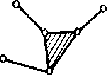
96. Начертите группу Ассура 2го класса, 1го вида.
Ответ: 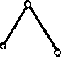
97. Начертите группу Ассура 2го класса, 2го вида.
Ответ: 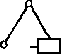
98. Начертите группу Ассура 2го класса, 3го вида.
Ответ: 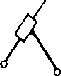
99. Начертите группу Ассура 2го класса, 4го вида.
Ответ:
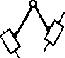
100. Начертите группу Ассура 2го класса, 5го вида.
Ответ: 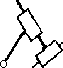
101. Как определяется класс механизма.
Ответ: по максимальному классу группы Ассура, входящей в механизм.
102. Назовите машины, с которыми Вы столкнетесь, работая по выбранной Вами специальности.
Ответ: двигатели внутреннего сгорания, гидротурбины и т.д.
103. Что это значит, если по формуле Чебышева Вы определили степень подвижности, и она равна 0.
Ответ: это значит, что ни одно звено не может двигаться относительно неподвижного звена, и кинематическая цепь превращается в ферму.
104. Что это значит, если по формуле Чебышева Вы определили степень подвижности, и она равна +2.
Ответ: это значит, что у механизма два ведущих звена.
105. Что это значит, если по формуле Чебышева Вы определили степень подвижности, и она равна –2.
Ответ:
106. Из скольких звеньев состоит группа Ассура 2го класса?
Ответ: 2.
107. Из скольких звеньев состоит группа Ассура 3го класса?
Ответ:4.
108. Из скольких звеньев состоит группа Ассура 4го класса?
Ответ:4.
109. Как определяется порядок группы Ассура?
Ответ: порядок равен числу поводков, которыми группа Ассура присоединяется.
4.8. Примеры решения задач по
структурному анализу механизма.
Пример 1. Определить класс механизма, ведущее звено 1 – ползун.
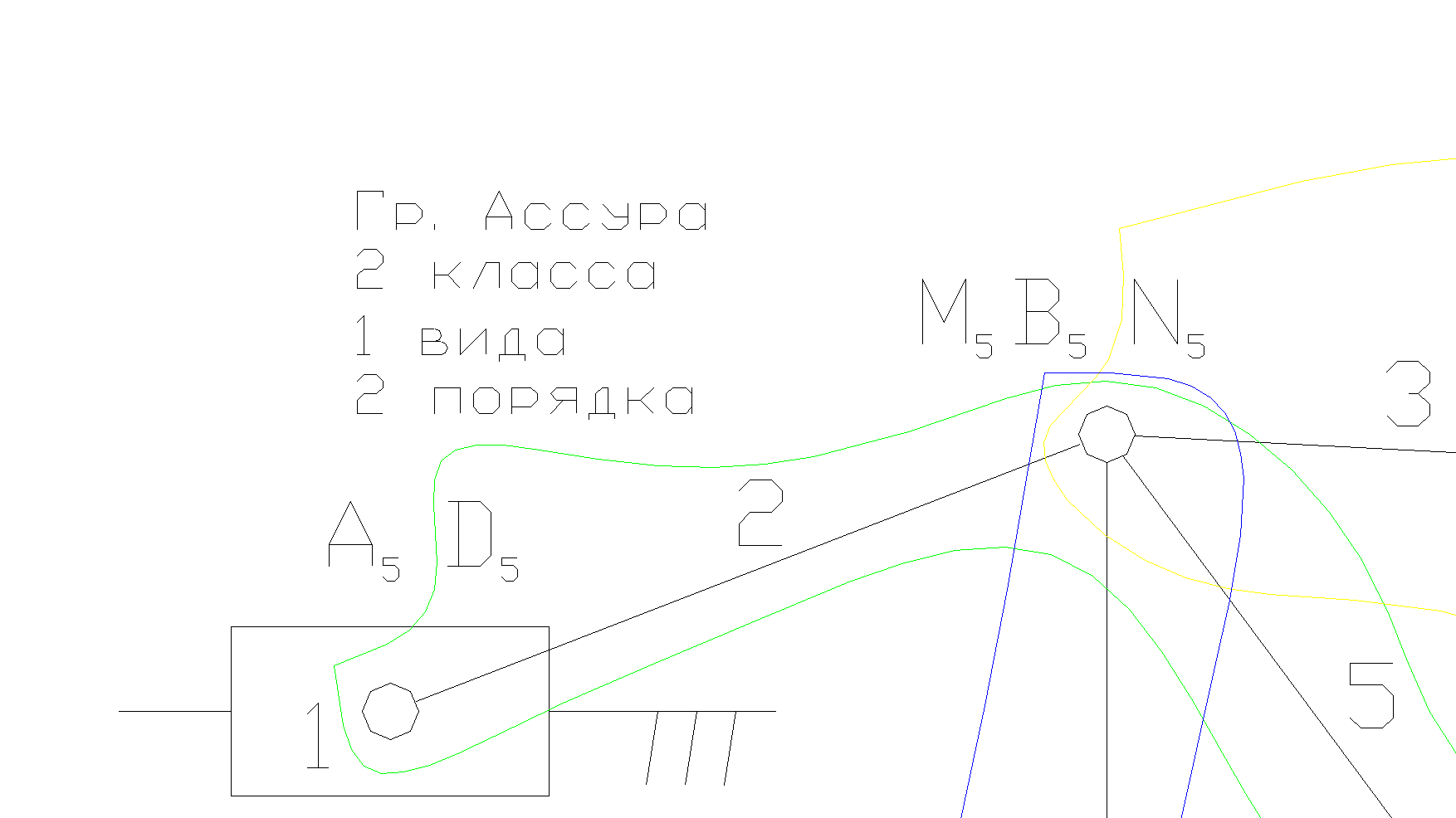
Решение.
1.Чертим структурную схему механизма.
2.Обозначаем все подвижные звенья механизма: 1 - ведущее звено ползун, это звено, которое совершает возвратно-поступательное движение,
2, 3, 6 – шатун, это звено, которое совершает сложное плоско-параллельное движение,
5, 7 – коромысло, это звено, которое совершает неполный оборот вокруг своей оси (качается).
3.Обозначаем все кинематические пары заглавными буквами латинского алфавита и указываем их класс: А5, С5 – кинематические пары 5-го класса низшие, поступательные,
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4.Определяем степень подвижности механизма по формуле Чебышева П.Л.:
W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1 – степень подвижности равна 1,
следовательно у механизма одно ведущее звено.
5.Лишних степеней свободы нет.
6.Пассивных связей нет.
7.Высших кинематических пар нет.
8.Отсоединяем последовательно три группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,5; 3,4. После отсоединения групп Асура остается ведущее звено 1 и стойка (начальный механизм или механизм первого класса).
9.Группы Ассура 3-го класса нет.
10.Группы Ассура 4-го класса нет.
11.Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Пример 2. Определить класс механизма, ведущее звено 4 – ползун.
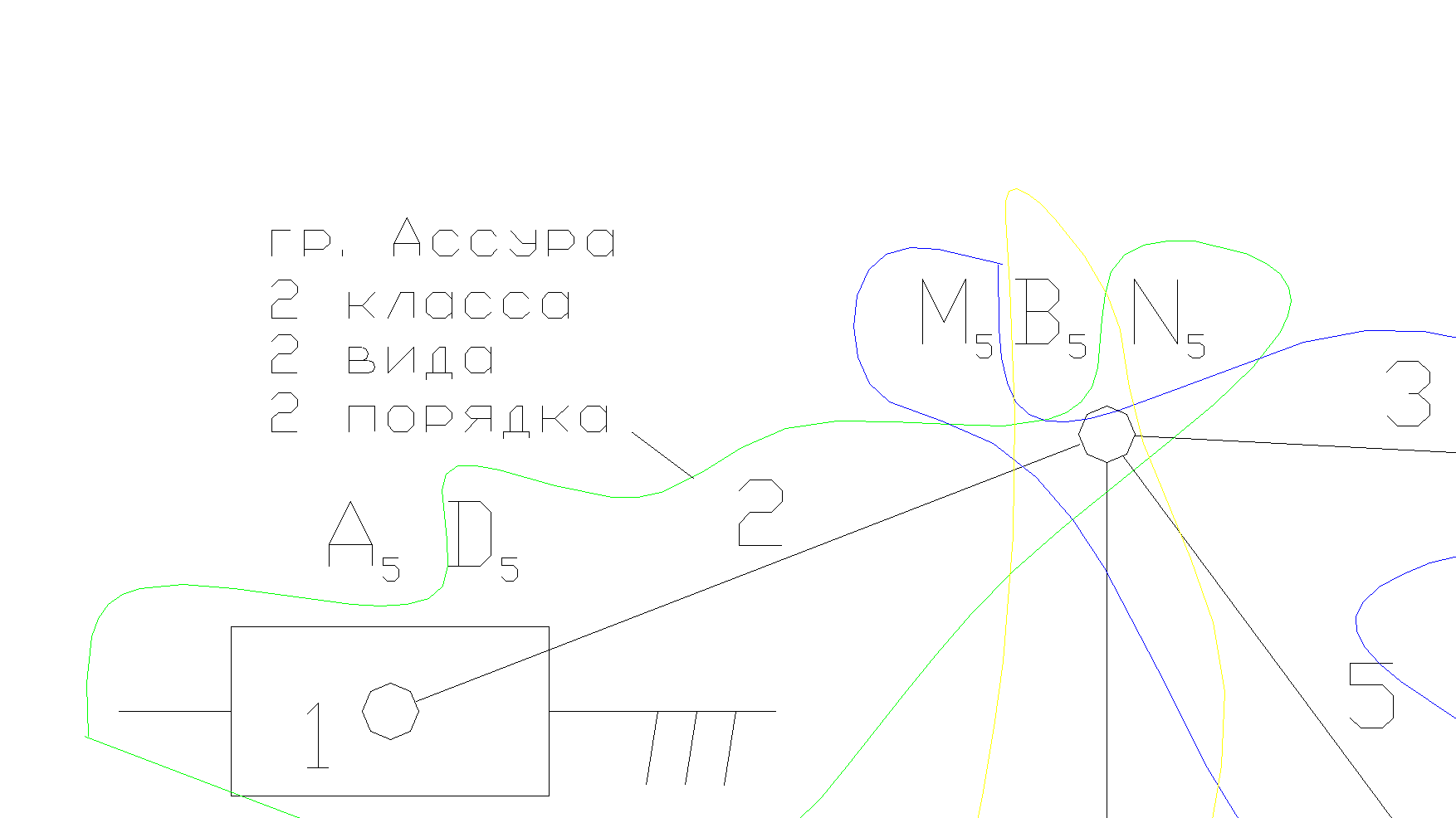
Решение.
1.Чертим структурную схему механизма.
2.Обозначаем все подвижные звенья механизма: 4 – ведущее звено ползун,
2, 3, 6 – шатун, 5, 7 – коромысло.
3.Обозначаем все кинематические пары: А5, С5 – кинематические пары 5-го класса низшие, поступательные, D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4.Определяем степень подвижности механизма:
W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5.Лишних степеней свободы нет.
6.Пассивных связей нет.
7.Высших кинематических пар нет.
8.Отсоединяем последовательно группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,1; 3,5. Осталось ведущее звено и стойка.
9.Группы Ассура 3-го класса нет.
10.Группы Ассура 4-го класса нет.
11.Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Пример 3. Определить класс механизма,
ведущее звено 5 – коромысло.
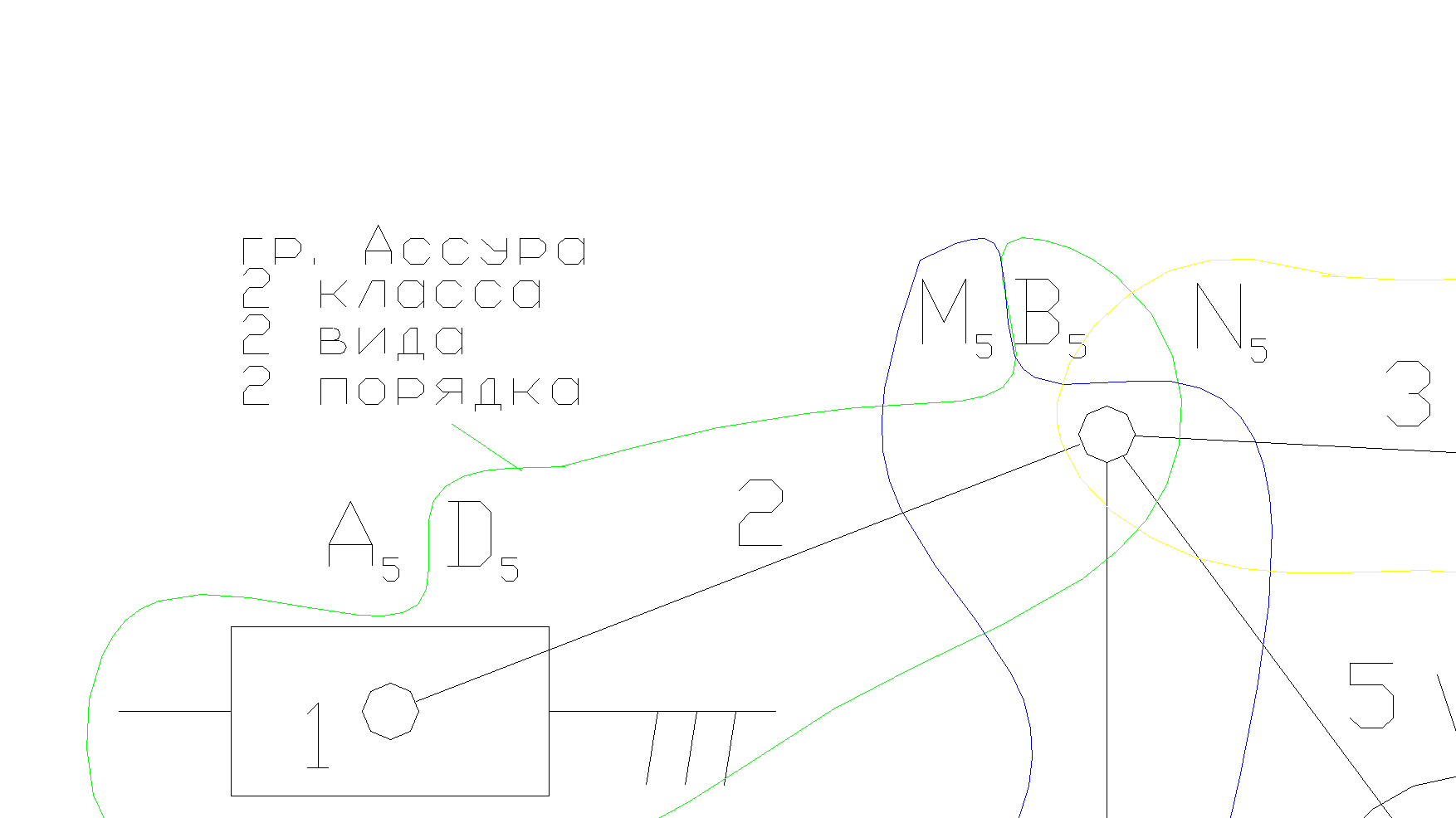
Решение.
1.Чертим структурную схему механизма.
2.Обозначаем все подвижные звенья механизма: 5 - ведущее звено коромысло, 1 – ползун, 2, 3, 6 – шатун, 5, 7 – коромысло.
3.Обозначаем все кинематические пары: А5, С5 – кинематические пары 5-го класса низшие, поступательные, D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4.Определяем степень подвижности механизма:
W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5.Лишних степеней свободы нет.
6.Пассивных связей нет.
7.Высших кинематических пар нет.
8.Отсоединяем последовательно группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,1; 3,4. Осталось ведущее звено и стойка.
9.Группы Ассура 3-го класса нет.
10.Группы Ассура 4-го класса нет.
11.Класс механизма 2-й, т.к. наивысший класс группы Ассура входящий в состав механизма 2-й.
Пример 4. Определить класс механизма,
ведущее звено 7 – кривошип.
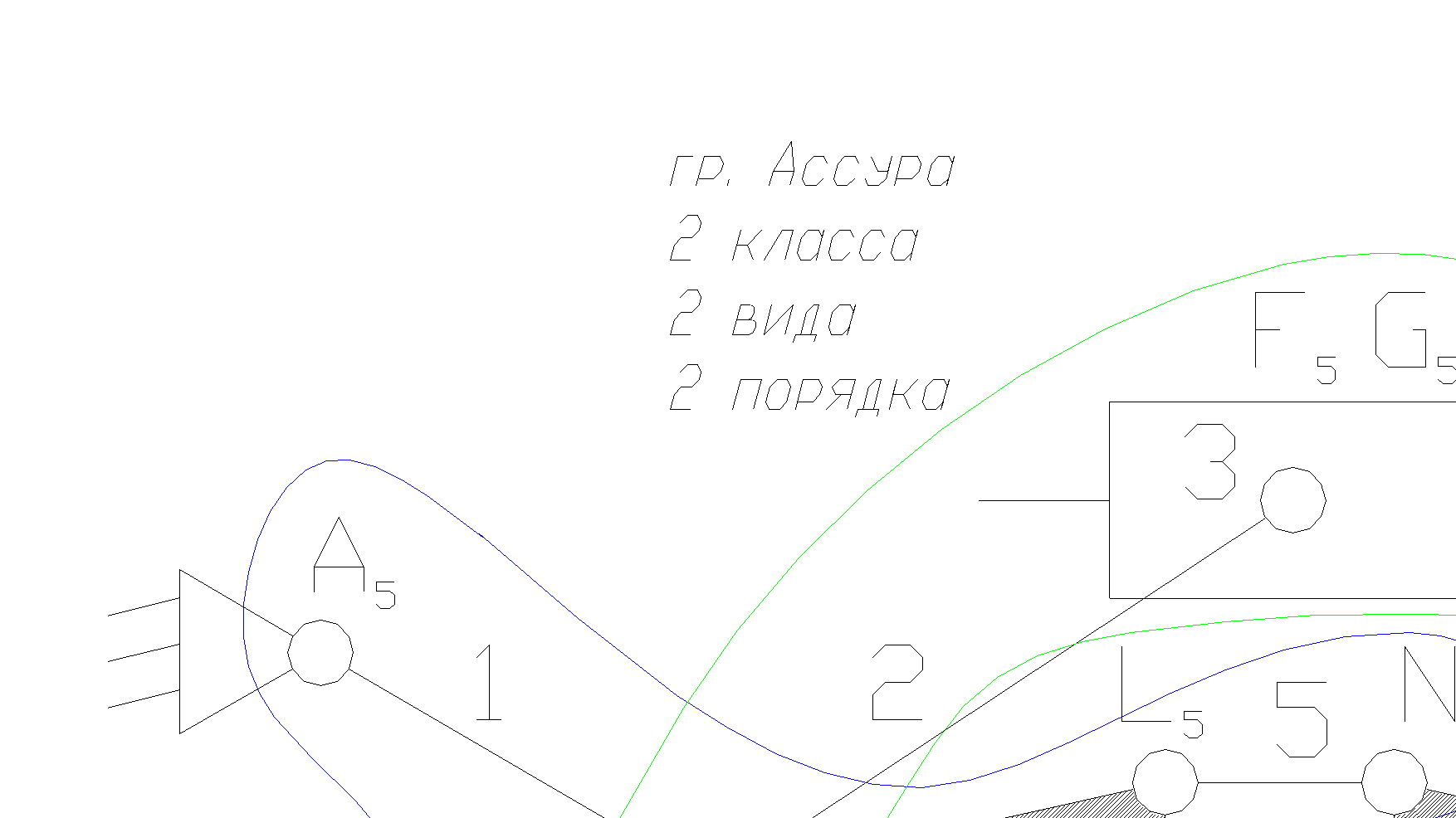
Решение.
1.Чертим структурную схему механизма.
2.Обозначаем подвижные звенья механизма: 7 - ведущее звено кривошип,
1 – коромысло, 2, 4, 5, 6 - шатун, 3 – ползун.
3.Обозначаем кинематические пары: A5, B5, C5, F5, K5, L5, N5, M5, H5 - кинематические пары 5-го класса низшие, вращательные, G5 - кинематическая пара 5-го класса низшая, поступательная.
4.Определяем степень подвижности механизма:
W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5.Лишних степеней свободы нет.
6.Пассивных связей нет.
7.Высших кинематических пар нет.
8.Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
9.Отсоединяем группу Ассура 3 класса, состоящую из звеньев 1,4,5,6. Осталось ведущее звено и стойка.
10.Группы Ассура 4-го класса нет.
11.Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Пример 5. Определить класс механизма, ведущее звено 1 – коромысло.
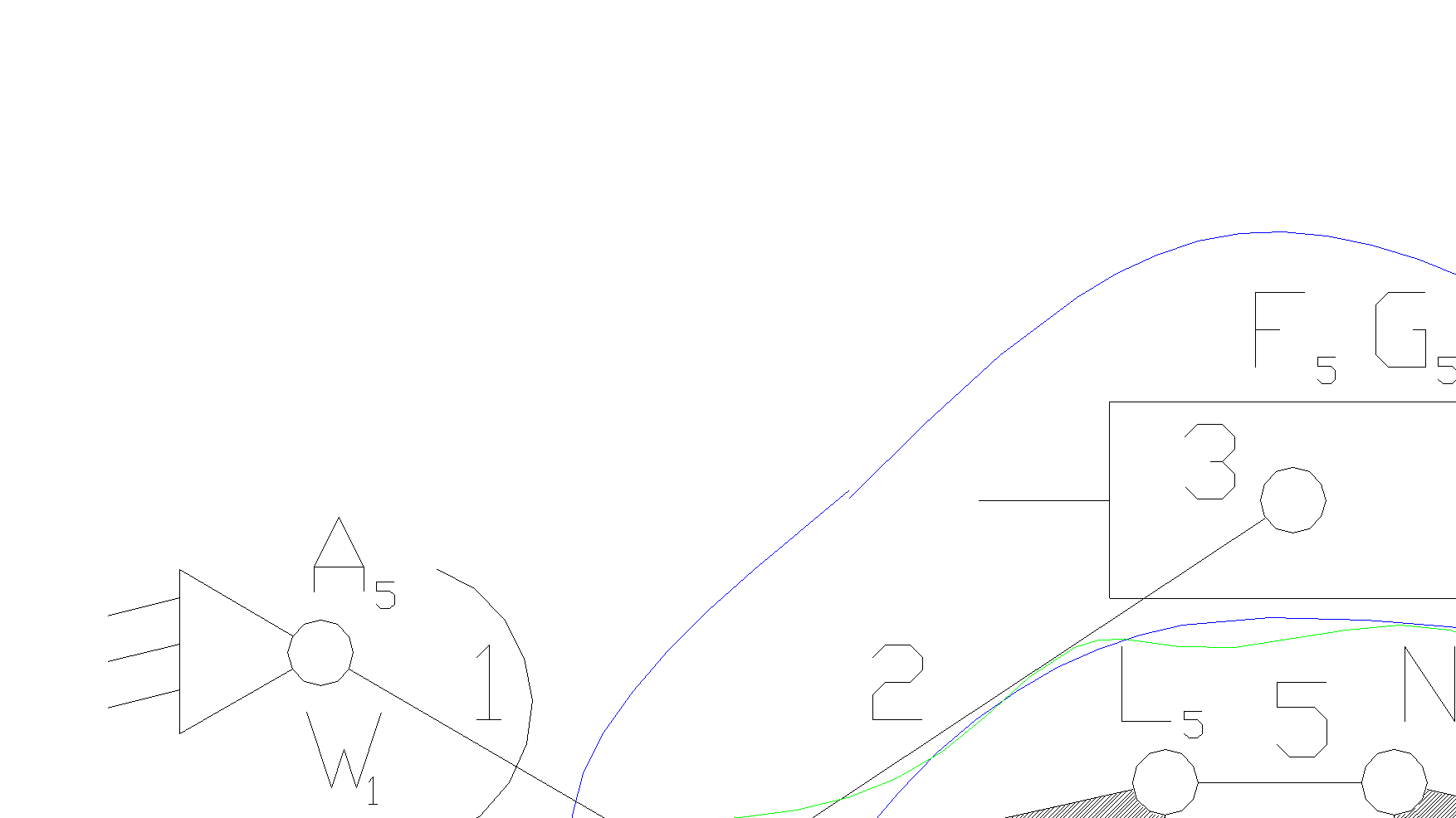
Решение.
1.Чертим структурную схему механизма.
2.Обозначаем подвижные звенья механизма: 1- ведущее звено коромысло, 2, 4, 5, 6 - шатун, 3 – ползун, 7 - кривошип.
3.Обозначаем кинематические пары: A5, B5, C5, F5, K5, L5, N5, M5, H5 - кинематические пары 5-го класса низшие, вращательные, G5 - кинематическая пара 5-го класса низшая, поступательная.
4.Определяем степень подвижности механизма:
W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5.Лишних степеней свободы нет.
6.Пассивных связей нет.
7.Высших кинематических пар нет.
8.Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
9.Группы Ассура 3-го класса нет.
10.Отсоединяем группу Ассура 4-го класса, состоящую из звеньев 4,5,6,7. Осталось ведущее звено и стойка.
11.Класс механизма 4-й, т.к. наивысший класс группы Асcура, входящий в состав механизма 4-й.
4.9. Цель и задачи кинематического анализа механизма. Цель кинематического анализа - изучить движение звеньев механизма, без учета сил, вызывающих это движение. Задачи: определение перемещений, скоростей, ускорений.
4.10. Методы кинематического анализа механизма. На практике применяют несколько методов: графический (или метод графиков и диаграмм), графоаналитический (или метод планов скоростей и ускорений), аналитический и экспериментальный.
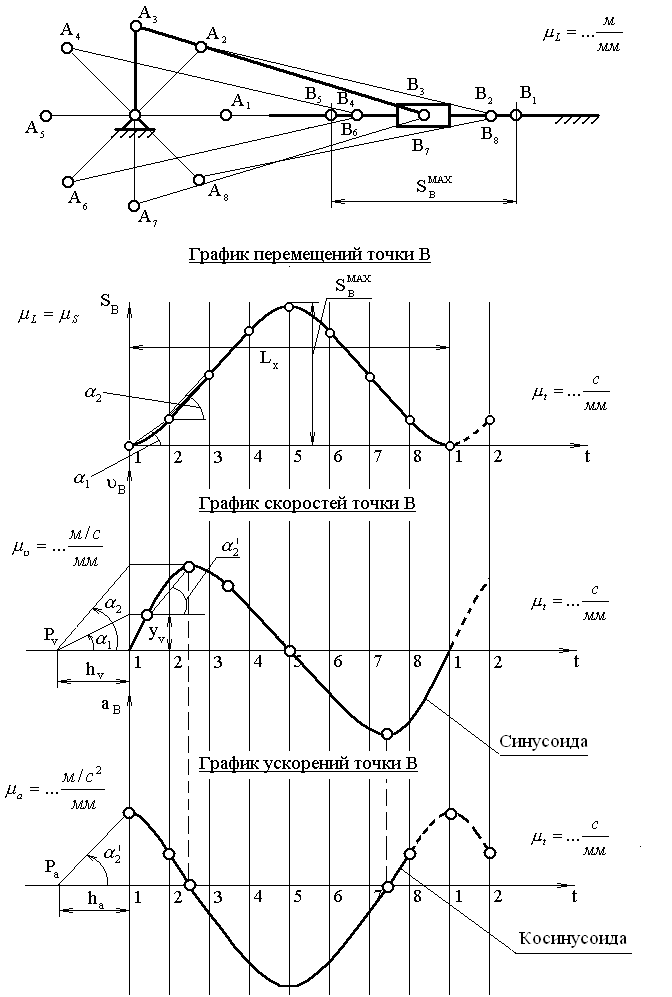
Рис.93. Пример графического метода кинематического анализа
Дата: 2019-02-25, просмотров: 658.