| Функции положения | Задача о скоростях | Задача об ускорения |
Определить функции положения:
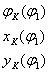
| Определение аналогов скоростей
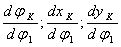Вычисление скоростей
| Определение
аналогов ускорений
 
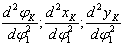Вычисление ускорений
|
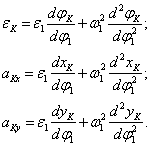
Как следует из приведенной таблицы, для решения задачи о положениях звеньев исследуемого механизма необходимо найти функции положения (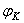 
или ХК и YК ), предварительно составив векторное уравнение замкнутого векторного контура кинематической цепи и уравнения проекций его на координатные оси Х и Y. Из этих уравнений находят функции положения (зависимости положений исследуемого звена от положения ведущего звена). При известном (заданном) законе движения ведущего звена задаются шагом и вычисляют координаты исследуемых звеньев (угловые координаты для вращающегося звена и прямоугольные для звена, совершающего возвратно-поступательное движение).
Для решения задачи о скоростях необходимо найти аналоги скоростей исследуемых звеньев и, умножив их на угловую скорость ведущего звена, получить формулы расчета искомых скоростей.
Для решения задачи об ускорениях находят также аналоги ускорений звеньев и по формулам, приведенным в таблице, находят величины ускорений.
Графическое дифференцирование и интегрирование.
Алгоритм графического дифференцирования:
| S |
| 2s |
| 3s |
| 1s |
| V |
| Кривая линия –исходный график |
0 1 2 3 4 5 6 7 8 j
0v 0 1 2 3 4 5 6 7 8 j
Hv
Рис.96. Графическое дифференцирование
1. На 1-ом графике кривую линию на каждом участке заменяем прямой.
2. На 2-ом графике выбираем полюсное расстояние HV=20¸40 мм.
3. Прямую 01S с 1-го графика параллельно переносим в точку 0V
2-го графика до тех пор пока она не пересечёт ось V.
Отрезок отсекаемый на оси V показывает значение скорости на
участке ( 01 ) 2-го графика.
4. Прямую 1S2S с 1-го графика параллельно переносим в точку 0V
2-го графика.
5. Аналогично поступаем на остальных участках.
6. Середины участков на 2-ом графике соединяем кривой линией.
Алгоритм графического интегрирования:
| 8 |
| 7 |
| 6 |
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 0 |
| j |
A
| 1A |
0A 0 1 2 3 4 5 6 7 8
HA
V
| j |
Рис. 97. Графическое интегрирование
1. На 1-ом графике кривую линию на каждом участке заменяем прямой.
2. На 1-ом графике выбираем полюсное расстояние Ha = 20¸40 мм.
3. Середину каждого участка на 1-ом графике параллельно сносим на ось A. Точку пересечения с осью A соединяем с точкой 0A.
4. Прямую 0A1A с 1-го графика параллельно переносим на участок 01 2- го графика.
5. На остальных участках поступаем аналогично.
Вопросы для самопроверки по кинематическому анализу механизма.
1. Цель кинематического анализа механизма.
Ответ: изучить движение звеньев механизма без учёта сил, вызывающих это движение.
2. Как называются графики, построенные по полученным значениям кинематических величин?
Ответ: кинематические диаграммы.
3. Назовите численные значения масштабного коэффициента.
Ответ: 1, 2, 2,5, 4, 5.
4. Как называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению ускорениям различных точек звеньев механизма в данный момент?
Ответ: план ускорений.
5. Единица измерения масштабного коэффициента скорости?
Ответ: м сек-1 / мм.
6. Напишите формулу для определения численного значения нормальной составляющей ускорения любой точки кривошипа.
Ответ: аn = w2. R
7. Как определить направления угловой скорости звена?
Ответ: угловая скорость и вектор относительной скорости
направлены в одну сторону.
8. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки кривошипа.
Ответ:
9. Скорость самолета 2500 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ: 694,4 м/сек.
10. Скорость автомобиля 80 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ: 22 м.
11. Задачи КАМ.
Ответ: определение перемещений звеньев и траекторий, описываемых точками звеньев; определение скоростей отдельных точек звеньев и угловых скоростей звеньев; определение ускорений отдельных точек звеньев и угловых ускорений звеньев.
12. Понятие масштабного коэффициента в ТММ?
Ответ: Масштабный коэффициент это отношение действительной величины к отрезку в мм, который изображает эту величину на чертеже.
13. Алгоритм графического интегрирования.
Ответ:
14. Напишите формулу для определения численного значения скорости любой точки кривошипа.
Ответ: V = w R.
15. Чем задаётся положение ведущего звена, если оно входит в поступательную пару?
Ответ: функцией перемещения s = s(t).
16. Как определить направления углового ускорения звена?
Ответ: угловое ускорение направлено в сторону тангенциальной составляющей относительного ускорения.
17. С какой целью определяют ускорения точек звеньев механизма?
Ответ: например, для определения силы инерции.
18. Сделайте чертеж и напишите векторное уравнение для определения ускорения любой точки кривошипа.
Ответ:
19. Скорость самолета 2400 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ: 666,7м/сек.
20. Скорость автомобиля 40 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ: 10 м.
21. Цель кинематического анализа механизма.
Ответ: изучить движение звеньев механизма без учёта сил, вызывающих это движение.
22. Алгоритм графического дифференцирования.
Ответ:
23. Для каких целей строят кинематические диаграммы?
Ответ: для кинематического исследования механизма.
24. Единица измерения масштабного коэффициента времени?
Ответ: сек / мм
25. Чем определяется положение ведущего звена, если оно входит во вращательную пару, со стойкой?
Ответ: функцией угла поворота j = j(t).
26. С какой целью определяют перемещения (траектории) точек звеньев механизма?
Ответ: для построения кинематических диаграмм, а также для выбора размеров корпусных деталей при проектировании механизма.
27. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки ползуна.
Ответ:
28. Скорость самолета 2300 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ: 638,9 м/сек.
29. Напишите формулу для определения угловой скорости w (рад./сек), если известна частота вращения n (об./мин.).
Ответ: w = 2 П n / 60
30. Скорость автомобиля 90 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ: 25 м.
31. Задачи КАМ.
Ответ:
32. Как называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент?
Ответ:
33. Единица измерения масштабного коэффициента длины?
Ответ: м / мм.
34. Напишите формулу для определения численного значения тангенциальной составляющей ускорения любой точки кривошипа.
Ответ: аt = Е R.
35. С какой целью определяют скорости точек звеньев механизма?
Ответ: например, для выбора типа смазки.
36. Сделайте чертеж и напишите векторное уравнение для определения ускорения любой точки ползуна.
Ответ:
37. Напишите формулу для определения угловой скорости звена, если известна частота вращения (об./мин.).
Ответ:
38. Скорость самолета 2200 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
39. Скорость автомобиля 50 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
40. Скорость пули 200 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ: 720 км.
41. Цель кинематического анализа механизма.
Ответ:
42. Единица измерения масштабного коэффициента угла поворота?
Ответ: град. / мм, или рад./мм.
43. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки шатуна.
Ответ:
44. Скорость самолета 2000 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
45. Скорость автомобиля 60 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
46. Скорость пули 220 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ:
47. Спортсмен пробегает 100 метров за 10 сек. А сколько километров спортсмен мог бы пробежать за один час, если бы двигался с такой же скоростью?
Ответ: 36 км.
48. Что такое кинематические диаграммы.
Ответ: графики, построенные по полученным значениям кинематических величин.
49. Что такое план скоростей?
Ответ: чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент?
50. Что такое план ускорений.
Ответ: чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению ускорениям различных точек звеньев механизма в данный момент?
51. Задачи КАМ.
Ответ:
52. Как называются графики, построенные по полученным значениям кинематических величин?
Ответ:
53. Понятие масштабного коэффициента в ТММ?
Ответ:
54. Что такое графическое дифференцирование?
Ответ:
55. Как называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент?
Ответ:
56. Единица измерения масштабного коэффициента угла поворота?
Ответ:
57. Сделайте чертеж и напишите векторное уравнение для определения ускорения любой точки шатуна.
Ответ:
57. Скорость самолета 1800 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
58. Скорость автомобиля 70 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
59. Скорость пули 240 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ:
60. Цель кинематического анализа механизма.
Ответ:
61. Кратный каким числам выбирается масштабный коэффициент?
Ответ:
62. Для каких целей строят кинематические диаграммы?
Ответ:
63. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки шатуна.
Ответ:
64. Скорость самолета 1700 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
65. Скорость автомобиля 100 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
66. Скорость пули 260 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ:
67. Спортсмен пробегает 100 метров за 11 сек. А сколько километров спортсмен мог бы пробежать за один час, если бы двигался с такой же скоростью?
Ответ:
68. Скорость самолета 1400 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
69. Скорость автомобиля 120 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
70. Скорость пули 300 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
4.13. Задачи для самостоятельного решения по кинематике механизмов: построить планы скоростей и ускорений для заданного положения механизма.
Задача 1.
4.14.Цель и задачи динамического анализа механизма. Цель - изучить движение звеньев механизма с учетом сил, вызывающих это движение. Задачи: силовой анализ механизма и динамика механизма.
При проектировании новых механизмов конструктор, выполнив структурный и кинематический анализы механизма, приступает к решению первой задачи динамического анализа, которая называется «Силовой анализ механизма». При этом он полагает, что:
- угловая скорость ведущего звена постоянна, то есть такая же, как и при кинематическом анализе механизма,
- задаваемые силы (движущие силы, силы сопротивления, силы тяжести звеньев, силы инерции) в механизме считаются известными, или их можно определить по известным формулам.
Исходя из принятых предположений, конструктор определяет:
1. Реакции в кинематических парах, знание которых позволяет ему выбрать размеры и массу звеньев и подшипников механизма, то есть провести расчет на прочность.
2. Уравновешивающую силу, под которой понимают условную силу, приложенную к ведущему звену механизма. Уравновешивающая сила в каждый момент времени уравновешивает все силы и моменты, действующие на звенья механизма, и следовательно, ведущее звено механизма в этом случае будет равномерно вращаться с постоянной угловой скоростью.
Решив первую задачу, конструктор приступает ко второй задаче, которая называется «Динамика механизма». При этом из решения первой задачи он знает размеры и массу, а следовательно, и моменты инерции звеньев механизма, а также все задаваемые силы (движущие, сопротивления, тяжести, инерции). По известным данным конструктор определяет истинный закон движения ведущего звена механизма, так как в реальных механизмах угловая скорость ведущего звена никогда не бывает постоянной, а все время колеблется между максимальным и минимальным значениями. Сравнив размах колебаний угловой скорости ведущего звена с допустимыми значениями для данного типа машин, конструктор прекращает дальнейший расчет, если укладывается в допустимые значения.
Если колебания угловой скорости ведущего звена спроектированного механизма превышают допустимые значения, то конструктор продолжает расчет. Суть дальнейшего расчета заключается в подборе размеров и массы маховика, который устанавливается на ведущее звено механизма, являясь аккумулятором кинетической энергии и дает возможность уменьшить размах колебаний угловой скорости ведущего звена до допустимых значений.
4.15.Определение сил, действующих на звенья механизма. Классификация сил в механизме.
Движущие силы направлены в сторону перемещения их точек приложения или составляют с этими перемещениями острые углы. Без движущих сил не работает ни одна машина. С энергетической стороны движущие силы совершают положительную работу. Движущие силы приложены к ведущим звеньям механизма.
Силы сопротивления направлены против перемещения их точек приложения или составляют с этими перемещениями тупые углы. С энергетической стороны силы сопротивления совершают отрицательную работу.
Силы сопротивления делятся на силы: производственных сопротивлений и силы трения. Силы производственных сопротивлений это те силы для преодоления которых и создан механизм, например: силы резания в токарном станке, силы прессования в прессах, силы строгания в строгальном станке. Эти силы часто задаются в виде графика для рабочего и холостого хода станка.
| Все силы, действующие в механизме |
| Задаваемые силы |
| Реакции связей |
| Движущие силы |
| Силы инерции звеньев |
| Силы тяжести звеньев |
| Силы сопротивления |
| Силы производственных сопротивлений |
| Силы трения |
Рис.98. Классификация сил, действующих на звенья механизма
Силы производственных сопротивлений приложены к исполнительным звеньям механизма. Силы трения (качения и скольжения, также определяются по известным формулам) возникают в кинематических парах. Часто в курсовых проектах, силами трения пренебрегают.
Силы тяжести звеньев приложены в центре масс звена (определяются по известным формулам: G ═ m·g) и могут совершать: положительную, отрицательную работы или не совершать никакой работы (если центр масс звена не перемещается или остается на одном горизонтальном уровне). С энергетической стороны силы тяжести звеньев совершают за период работы механизма столько же положительной работы, сколько и отрицательной.
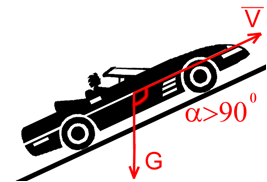
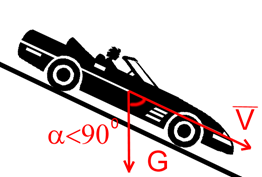
Рис.99. Сила тяжести звеньев
Дата: 2019-02-25, просмотров: 442.
