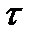
|
| n |
| S2 |
| П, O |
| a |
| b |
| Mn2 |
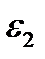
|
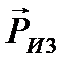
|
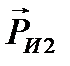
|
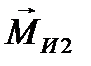
|
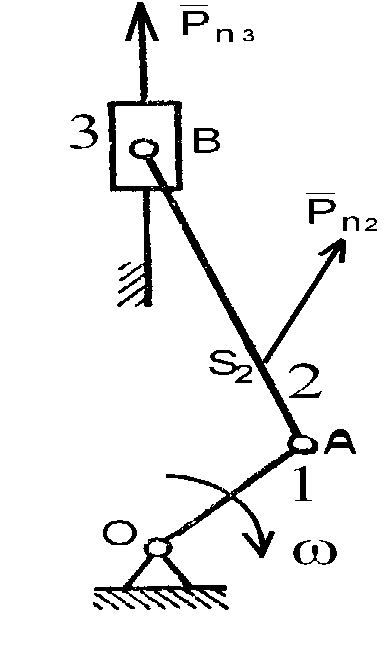
Рис.100. Силы инерции и моменты пар сил инерции, действующие
на звенья кривошипно-шатунного механизма
Силы инерции и момент пары сил инерции возникает, если у звена имеется масса и звено движется. Силы инерции за период работы механизма могут совершать положительную, отрицательную работы или не совершать никакой работы.
Силы инерции определяются по формуле:
→ →
Pи ═ ― m·as ,
где:
→
Pи - вектор силы инерции,
m - масса звена,
→
as - вектор ускорения центра масс звена.
Так как центр масс кривошипа (звено 1), находится в точке О, ускорение которой равно нулю. То и сила инерции, действующая на кривошип также равна нулю.
Центр масс шатуна (звено 2) находится в точке S2. Тогда вектор силы инерции, действующей на шатун будет направлен в противоположную сторону ускорения точки S2, показанного на плане ускорений.
Аналогично, вектор силы инерции, действующей на ползун (звено 3) будет направлен в противоположную сторону ускорения точки В, показанный на плане ускорений.
Момент пары сил инерции определяется по формуле:
Mи ═ ― Ԑ·Jх ,
где:
Mи - момент пары сил инерции,
Ԑ - угловое ускорение звена,
Jх - момент инерции звена, относительно оси, проходящей через
центр тяжести звена.
Так как угловая скорость кривошипа (звено 1) постоянна, то угловое ускорение равно нулю. В этом случае, момент пары сил инерции на кривошип не действует.
Так как угловое ускорение шатуна (звено 2) направлено по часовой стрелке в сторону тангенциальной составляющей ускорения τ, то момент пары сил инерции будет направлен против углового ускорения, то есть против часовой стрелки.
Угловое ускорение ползуна (звено 3) отсутствует, так как ползун совершает возвратно-поступательное движение и не вращается. В этом случае, момент пары сил инерции на ползун действовать не будет.
Для примера покажем, как будет направлен момент пары сил инерции, действующий на вращающийся диск (колесо автомобиля, ротор турбины) (рис.101).
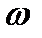
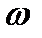
|
|
| MИШ |
|
| MИ |
|
Рис.101. Направление действия момента пар сил инерции на вращающийся диск
4.17. Графоаналитический метод кинетостатического расчета механизма. В ТММ силовой расчет механизма основывается на принципе
Д,Аламбера, сущность которого заключается в следующем: если к звеньям механизма мысленно приложить еще и силы инерции, то сумма всех сил, действующих на механизм будет равна нулю. Этот метод называется еще кинетостатическим расчетом механизма, в отличие от статического расчета, когда не учитываются силы инерции звеньев. Этот расчет достаточно трудоемкий и в курсовом проекте по ТММ этот расчет выполняется на отдельном листе формата А1.
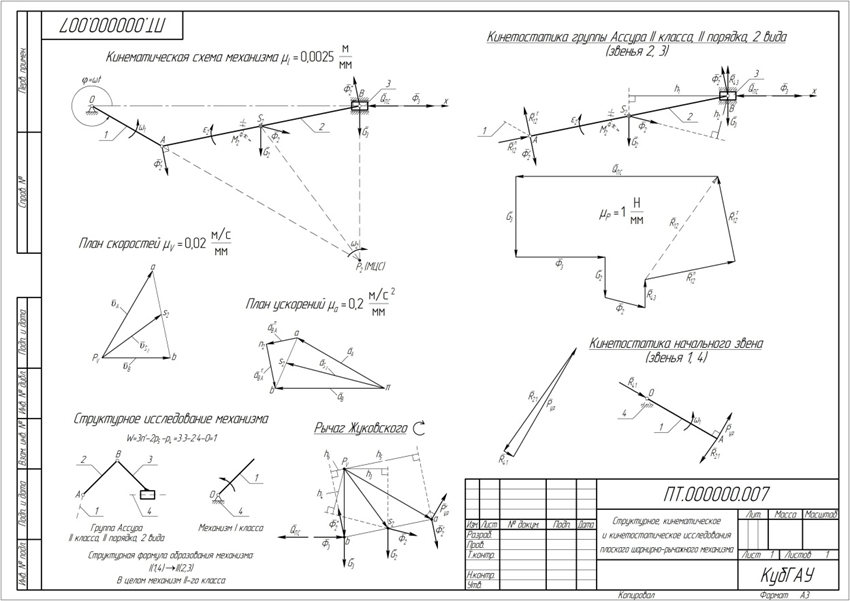
Рис.102. Пример кинетостатического расчета механизма
Графоаналитическим методом
Порядок кинетостатического расчета механизма. Группа Ассура является статически определимой кинематической цепью. Поэтому алгоритм расчета следующий:
Шаг 1: провести структурный анализ механизма.
Шаг 2: провести кинематический анализ механизма и определить значения ускорений.
Шаг 3: провести силовой расчет последней группы Ассура, затем предпоследней и так до тех пор, пока не останется ведущее звено и стойка.
Шаг 4: провести силовой расчет ведущего звена.
Реакции в кинематических парах механизма. Если не учитывать силу трения при кинетостатическом расчете механизма, то:
- во вращательной кинематической паре 5-го класса реакция одного звена на другое проходит через центр шарнира, а неизвестны: величина и направление реакции,
- в поступательной кинематической паре 5-го класса реакция перпендикулярна к оси относительного движения звеньев, а неизвестны: величина и точка приложения реакции,
- в высшей кинематической паре 4-го класса реакция приложена в точке касания звеньев и направлена по нормали, проведенной через точку касания, неизвестна величина реакции.
Порядок силового расчета группы Ассура.
Шаг 1: отсоединить группу Ассура от механизма и приложить к ней известные силы, в том числе и силы инерции, а действия звеньев заменить реакциями.
Шаг 2: найти сумму моментов всех сил, действующих на одно звено группы Ассура, относительно точки (кинематической пары, так чтобы из полученного уравнения можно было найти значение тангенциальной составляющей реакции).
Шаг 3: составить векторное уравнение всех сил, действующих на группу Ассура, которое равно нулю. В векторное уравнение войдут два неизвестных вектора, их пересечение при графическом построении даст нам решение векторного уравнения.
Порядок силового расчета ведущего звена. Условно в ТММ за ведущее звено принимается звено (кривошип), к которому подводится движение извне и которое приводит в движение механизм рабочих машин, или звено (кривошип) от которого передается движение наружу (вовне) механизма двигателя.
Шаг 1: отсоединить ведущее звено от стойки, а действие стойки заменить реакцией.
Шаг 2: приложить к ведущему звену известные силы.
Шаг 3: приложить к ведущему звену силу реакции группы Ассура, равную по величине, но направленную в противоположную сторону силы реакции ведущего звена на группу Ассура, которую определили в результате расчета группы Ассура.
Шаг 4: приложить к ведущему звену в любой точке, кроме оси вращения кривошипа, неизвестную по величине и направлению уравновешивающую силу.
Шаг 5: найти сумму моментов всех сил, действующих на ведущее звено, относительно оси вращения кривошипа. Из этого уравнения определим уравновешивающую силу.
Шаг 6: составить векторное уравнение всех сил, действующих на ведущее звено, которое равно нулю. Из уравнения найдем реакцию стойки на ведущее звено.
4.18. Определение уравновешивающей силы по теореме Жуковского. Теорема Жуковского звучит следующим образом: «Если в соответствующие точки плана скоростей механизма, повернутого относительно полюса на 90 градусов, параллельно самим себе перенести все силы, действующие на звенья механизма, включая силы инерции и уравновешивающую силу, которая неизвестна, то сумма моментов всех сил относительно полюса равна нулю.»
Алгоритм определения уравновешивающей силы:
1. Построить план скоростей.
2. Повернуть план скоростей относительно полюса на 90о.
3. В соответствующие точки плана скоростей перенести параллельно самим себе все силы, действующие на звенья механизма.
4. Найти сумму моментов всех сил относительно полюса.
5. Решить уравнение и найти значение уравновешивающей силы.
Дата: 2019-02-25, просмотров: 526.