Таким образом, хрупкий и пластично-хрупкий материалы не имеют площадки текучести, а в справочниках отсутствует характеристика «предел текучести». По этой особенности их можно узнать.
Пластично-хрупкие материалы значительно деформируются, этого нельзя допустить в работающей конструкции. Поэтому их деформацию обычно ограничивают. Максимально возможная относительная деформация ε = 0,2%. По величине максимально возможной деформации определяется соответствующее нормальное напряжение σ0,2, которое принимают за предельное.
3.16.Предельные и допустимые напряжения. Предельным напряжением считают напряжение, при котором в материале возникает опасное состояние (разрушение или опасная деформация).
Для пластичных материалов предельным напряжением считают предел текучести, т.к. возникающие пластические деформации не исчезают после снятия нагрузки.
Для хрупких материалов, где пластические деформации отсутствуют, а разрушение возникает по хрупкому типу, за предельное напряжение принимают предел прочности.
Для пластично-хрупких материалов предельным напряжением считают напряжение, соответствующее максимальной деформации 0,2% .
Допускаемое напряжение - максимальное напряжение, при котором реальная конструкция или деталь должны нормально работать.
Допускаемые напряжения получают по предельным с учетом запаса прочности:
σ предельное
[σ] ═ ――――,
[ s ]
где:
[σ] - допускаемое напряжение,
[s] – допускаемый коэффициент запаса прочности.
Допускаемый коэффициент запаса прочности зависит от качества материала, условий работы детали, назначения детали, точности обработки и расчета и т. д. и выбирается конструктором под свою ответственность. Он может колебаться от 1,25 для простых деталей до 12,5 для сложных деталей, работающих при переменных нагрузках в условиях ударов и вибраций.
3.17.Особенности поведения материалов при испытаниях на сжатие. Пластичные материалы практически одинаково работают при растяжении и сжатии. Механические характеристики при растяжении и сжатии одинаковы. Хрупкие материалы обычно обладают большей прочностью при сжатии, чем при растяжении: σвр < σвс. Если допускаемое напряжение при растяжении и сжатии различно, их обозначают [σр] (растяжение), [σс] (сжатие).
3.18.Расчеты на прочность при растяжении и сжатии. В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы из-за опасной деформации детали или разрушение детали.
Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких - предел прочности.
Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации наибольшие напряжения (рабочие напряжения или действующие напряжения) были меньше предельных в [s] раз, то есть меньше допускаемых напряжений. Тогда расчетная формула при растяжении и сжатии имеет вид:
σ = N / А ≤ [σ],
и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле: σ = N /А, не должно превышать допустимое (допускаемое).
На практике расчеты на прочность проводят для решения трех задач:
проектный расчет, при котором определяются минимальные размеры опасного сечения,
проверочный расчет, при котором определяется рабочее напряжение и сравнивается с предельно допустимым,
определение допускаемой нагрузки при заданных размерах опасного сечения.
3.19.Основные предпосылки расчетов на сдвиг (срез) и смятие. Если детали соединений: болты, штифты, шпонки, заклепки работают так, что можно учитывать только один внутренний силовой фактор - поперечную силу Q, то такие детали рассчитываются на сдвиг (срез).
Сдвиг - такая деформация детали, когда ее плоские слои смещаются параллельно друг другу.
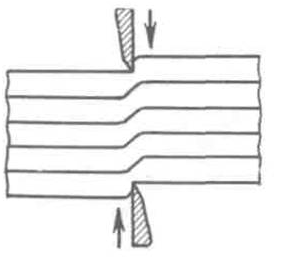
Рис.48. Пример деформации сдвига:
при резке ножницами бумаги или листовой стали
3.20.Сдвиг. Закон Гука при сдвиге. На сечения бруса действуют поперечные силы, вызывающие касательные напряжения τ в поперечном сечении бруса. Грани бесконечно малой площадки в поперечном сечении сдвигаются на угол ɣ, который называют углом сдвига.
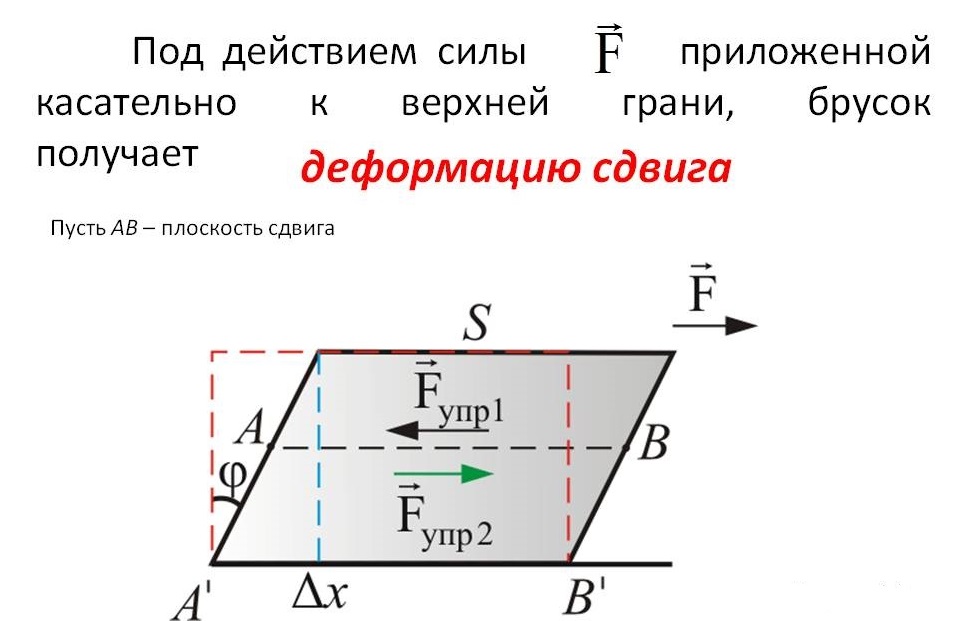
Рис.49. Деформация сдвига
В области упругих деформаций выполняется Закон Гука при сдвиге:
τ ═ G·ɣ,
где:
τ - касательное напряжение, (МПа),
Ԍ - модуль упругости сдвига, (Мпа), (модуль упругости второго рода),
Ԍ = 0,4 Е,
где: Е – модуль упругости при растяжении, (Мпа),
ɣ - угол сдвига (безразмерная величина).
Основные допущения при расчете деталей на сдвиг:
- при расчете на сдвиг изгиб детали не учитывается,
- силы упругости распределены по сечению равномерно,
- если при сдвиге нагружены несколько деталей (например, несколько болтов или заклепок), то внешняя сила распределяется между ними равномерно.
3.21.Расчет касательных напряжений при сдвиге:
τ ═ Q / A ,
где:
Q - поперечная сила,
A - площадь сдвига.
Q ═ F / n ,
где:
F - внешняя сила,
n - количество нагруженных деталей.
3.22.Условие прочности при сдвиге:
τ ═ Q/A ≤ [τ],
где:
τ - действующее касательное напряжение сдвига,
Q - поперечная сила,
A - площадь сдвига,
[τ] - допускаемое напряжение сдвига, [τ] ═ 0,3σт,
где:
σт - предел текучести материала при растяжении.
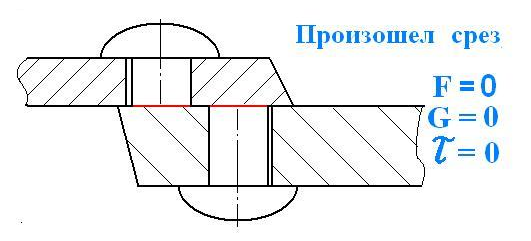
Рис.50. Срез заклепки
В области упругих деформаций происходит сдвиг. При снятии внешней нагрузки, деталь принимает первоначальный вид.
В случае, если внешняя сила продолжает увеличиваться, то наступает пластическая деформация и деталь разрушается (перерезается поперек). Такой вид разрушения называется срез.
3.23.Смятие. Если, рассчитываемая деталь соединяет пластины, то одновременно со сдвигом происходит смятие боковой поверхности детали в месте контакта с пластинами. На поверхности детали (болт, заклепка, и т.д.) возникают сжимающие напряжения, называемые напряжениями смятия - σсм.
Если деталь имеет цилиндрическую поверхность, то при расчете на смятие, вместо боковой поверхности цилиндра в расчете используют плоскую поверхность, проходящую через диаметр.
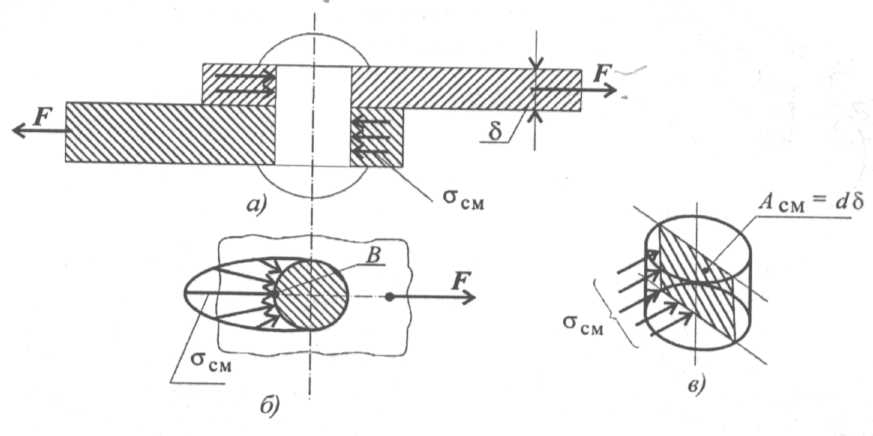
Рис.51. Смятие заклепки:
а, б – напряжения смятия, в – площадь смятия
3.24.Условие прочности при смятии:
σ ═ F/A ≤ [σ],
где:
σ – действующее напряжение смятия, (Мпа),
F – внешняя сила,
A – площадь смятия детали,
где: A ═ dδ,
d – диаметр детали,
δ – наименьшая высота соединяемых пластин,
[σ] – допускаемое напряжение смятия,
где:
[σ] ═ 0,4 σт.
σт - предел текучести материала при растяжении.
3.25.Пример расчета детали, работающей на срез и смятие (шпонка). Ширину (b) и высоту (h) ненапряженной шпонки принимают по ГОСТу в зависимости от диаметра вала (d), а длину (L) шпонки рассчитывают из условия прочности: то есть должно обеспечиваться отсутствие среза и смятия.
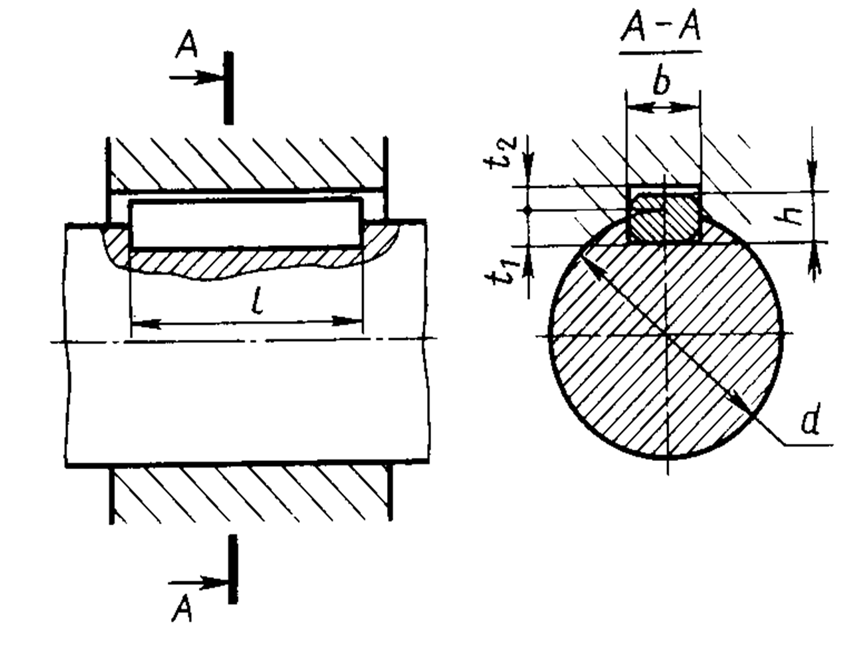
Рис.52. Расчет шпонки на срез и смятие
Внешнее усилие, действующее на шпонку, связано с вращающим моментом зависимостью:
F ═ 2M / d,
где:
М – вращающий момент,
d – диаметр вала.
Площадь среза (А среза) шпонки определяют по формуле:
А среза = L · b ,
где:
L – длина шпонки,
b – ширина шпонки.
Площадь смятия (А смятия) шпонки определяют по формуле:
А смятия = L · ( h - t 1 ),
где:
L – длина шпонки,
t1 – глубина шпоночного паза вала,
h – высота шпонки,
h-t1 - часть шпонки, которая выступает за пределы вала.
В результате получаем формулы для расчета призматических шпонок на:
- сдвиг (срез): τ ═ 2М/dLb ≤ [τ],
- и смятие: σ ═ 2М/dL(h―t1) ≤ [σ]
Дата: 2019-02-25, просмотров: 474.