Иногда приходится исследовать равновесие нетвердых тел. При этом будем пользоваться предположением, что если это нетвердое тело находится в равновесии под действием сил, то его можно рассматривать как твердое тело, используя все правила и методы статики.
Связи, как и другие понятия, встречающиеся в аксиомах, являются абстракциями, весьма условно отражающими свойства реальных объектов. Например, рассмотренная выше гибкая невесомая нить может быть моделью подвесных и вантовых систем, у которых масса погонного метра троса составляет десятки и сотни килограммов. Однако усилия, возникающие в таких тросах, во столько раз больше их собственного веса, что при расчете последним можно пренебречь, считая их невесомыми.
Пример 1. На невесомую арку с тремя шарнирами действует горизонтальная сила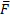 
(рис.19). Определить линию действия реакции 
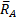(реакции связи в точке А).
Решение: Рассмотрим правую часть арки отдельно. В точках В и С приложим силы реакции связей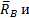 
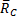. Тело под действием двух сил находится в равновесии. Согласно аксиоме о равновесии двух сил, силы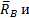 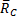равны по величине и действуют вдоль одной прямой в противоположные стороны. Таким образом, направление силы 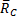нам известно (вдоль линии ВС).
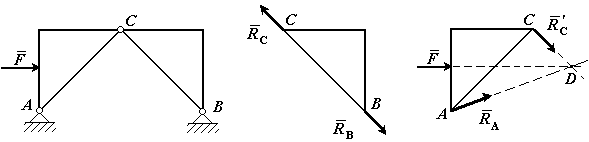
Рис.19. Арка с тремя шарнирами
Рассмотрим левую часть арки отдельно. В точках А и С приложим силы реакции связей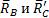 
. Сила 
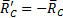, действие равно противодействию. На тело действуют три силы, направления двух сил ( 
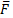и 
) и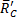звестно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила 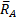направлена вдоль линии AD.
Пример 2. Однородный стержень закреплен шарнирно в точке А и опирается на гладкий цилиндр. Определить линию действия реакции 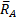(реакции связи в точке А), смотри (рис. 20).
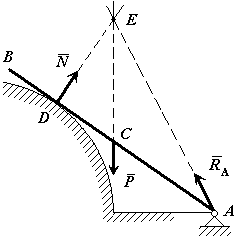
Рис.20. Реакции стержня, закрепленного в шарнире
Решение: Так как стержень однородный, то равнодействующая сил тяжести (сила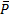 
), действующих на стержень, приложена в его геометрическом центре (точка С). Так как стержень опирается на гладкую поверхность, то реакция связи (сила 
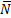) в точке касания (точка D) направлена по нормали к этой поверхности. На тело действуют три силы, направления двух сил ( 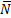и .) и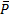звестно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила 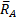направлена вдоль линии A Е.
2.5. Основные понятия кинематики. Очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее кто-то толкнул. Абсолютно все равно.
К основным понятиям кинематики относятся: траектория, радиус-вектор, закон движения тела.
Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
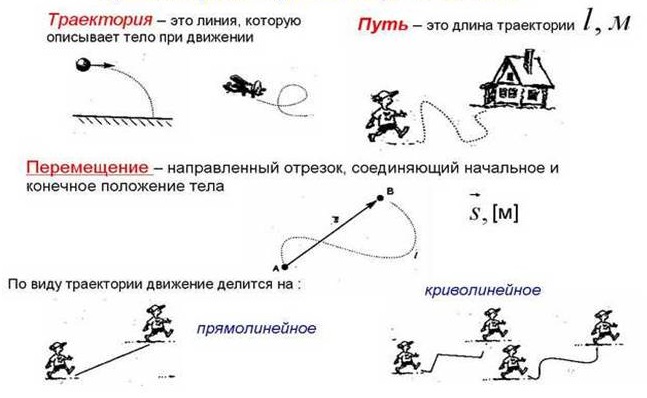
Рис.21. Траектория, путь, перемещение
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения. В системе СИ перемещение и длина пути измеряются в метрах. Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло.
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость (скорость в данный момент времени) – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
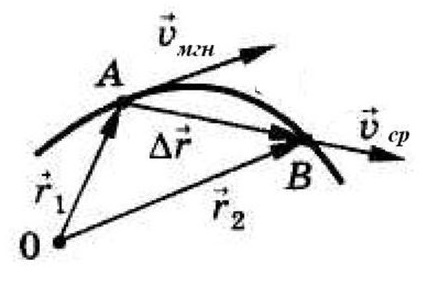
Рис.22. Средняя и мгновенная скорости
В системе СИ скорость измеряется в метрах в секунду. Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение (изменение скорости за единицу времени) показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают.
Рис.23. Ускорение
В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории в сторону углового ускорения (перпендикулярно нормальному ускорению).
Нормальное же ускорение характеризует быстроту изменения скорости по направлению и всегда направлено к центру вращения.
Вектор нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
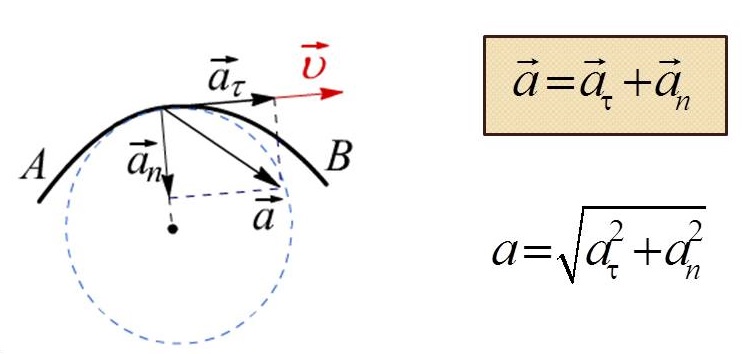
Рис.24. Тангенциальное, нормальное и полное ускорения
2.6. Основные понятия динамики. Динамика — раздел теоретической механики, в котором, устанавливается связь между движением тел и действующими на них силами.
В динамике решают два типа задач:
— определяют параметры движения по заданным силам;
— определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
2.7. Аксиомы динамики. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею.
Первая аксиома (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния. Это состояние называют состоянием инерции. Вывести точку из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела. Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома (второй закон Ньютона — основной закон динамики). Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая: F=ma, где m — масса точки, кг; а — ускорение точки, м/с2. Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли: F тяж = mg, где g — 9,81 м/с² , ускорение свободного падения.
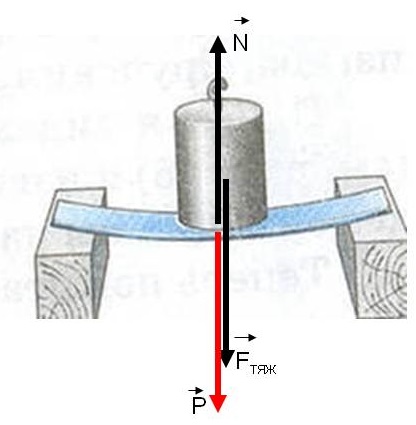
Рис.25. Сила тяжести и вес тела
Сила тяжести (F тяж) вызвана взаимодействием тела с Землей, приложена к центру масс тела и направлена к центру Земли.
Вес тела (Р) вызван взаимодействием тела и опоры. Вес тела приложен к опоре. Если опора покоится или движется с постоянной скоростью, то вес тела равен силе тяжести. Если опора движется с ускорение, то вес тела может быть: больше силы тяжести, меньше силы тяжести или равен нулю.
Сила реакции опоры ( N ) (сила упругости) приложена к телу и направлена в противоположную сторону силе веса тела.
Третья аксиома (третий закон Ньютона). Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны.
Четвертая аксиома (закон независимости действия сил). Каждая сила системы сил действует так, как она действовала бы одна. Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности.
2.8. Силы трения. Абсолютно гладких и абсолютно твердых тел в природе не существует, и поэтому при перемещении одного тела по поверхности другого возникает сопротивление, которое называется трением.
Трение — это явление сопротивления относительному перемещению, возникающее между двумя телами в зонах соприкасания поверхностей по касательной к ним.
Трение чрезвычайно распространено в природе и имеет большое значение. На трении основана работа ременных и фрикционных передач, тормозных устройств, прокатных станов, наклонных транспортеров, фрикционных муфт и т. п. Трение обеспечивает сцепление с землей и, следовательно, работу автомобилей, тракторов и других транспортных машин. При отсутствии трения человек не мог бы ходить. Наряду с этим трение во многих случаях является вредным сопротивлением, на преодоление которого затрачивается нередко весьма большое количество энергии. Эти затраты энергии бесполезны, и их стремятся уменьшить.
Трение классифицируется по наличию и характеру движения.
Трением покоя называется трение двух тел при микросмещениях без макросмещения, т. е. при малом относительном перемещении тел в пределах перехода от покоя к относительному движению.
Трением движения называется трение двух тел, находящихся в относительном движении.
Рассмотрим виды трения в зависимости от наличия и характера относительного движения.
Трением скольжения называется трение движения, при котором скорости тел в точке касания различны по значению и (или) направлению.
Трение скольжения, как и трение покоя, обусловлено прежде всего шероховатостью и деформацией поверхностей, а также наличием молекулярного сцепления у прижатых друг к другу тел. Трение скольжения сопровождается изнашиванием, т. е. отделением или остаточной деформацией материала, а также нагревом трущихся поверхностей тел (остаточной называется деформация, не исчезающая после прекращения действия внешних сил).
Трение характеризуется силой трения. Причина – механическое зацепление выступление выступов.
Сила трения есть сила сопротивления относительному перемещению двух тел при трении.
Возьмем тело, лежащее на горизонтальной шероховатой плоскости. Сила тяжести G уравновешивается нормальной реакцией N. Если к телу приложить небольшую движущую силу F, то оно не придет в движение, так как эта сила будет уравновешиваться силой трения FТР. Сила трения является, таким образом, реакцией опорной плоскости, направленной вдоль плоскости. Если постепенно увеличивать сдвигающую силу F, то до определенного ее значения тело будет оставаться в покое; при дальнейшем увеличении силы F тело придет в движение.
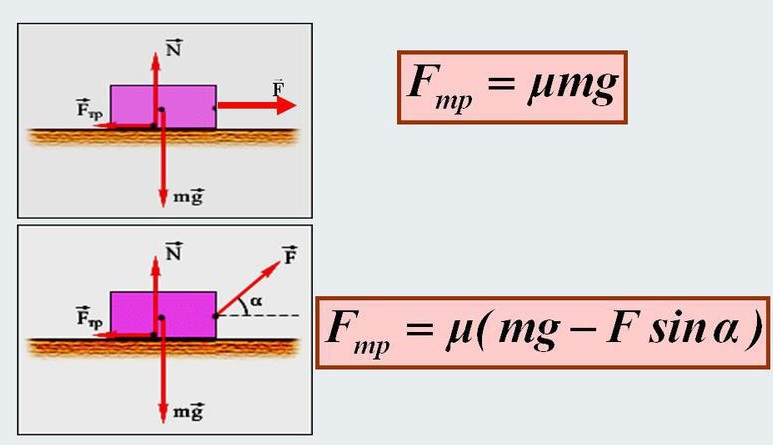
Рис.26. Сила трения скольжения
Отсюда видно, что сила трения в состоянии покоя в зависимости от степени предварительного смещения (микросмешения) может изменяться от нуля до какого-то максимального значения, причем по модулю Fтр всегда равна сдвигающей силе F .
Максимальное значение сила трения покоя имеет в момент начала относительного движения и называется наибольшей силой трения покоя или просто силой трения покоя.
Сила трения всегда направлена в сторону, противоположную направлению относительного движения тела.
Сила трения качения — сила сопротивлению движения, возникающая при перекатывании тел друг по другу
,
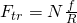где:
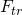— сила трения качения,
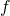— Коэффициент трения качения,
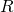— радиус тела,
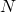— реакция опоры.
Происхождение трения качения можно наглядно представить себе так. Когда шар или цилиндр катится по поверхности другого тела, он немного вдавливается в поверхность этого тела, а сам немного сжимается. Таким образом, катящееся тело все время как бы вкатывается на горку. Вместе с тем происходит отрыв участков одной поверхности от другой, а силы сцепления, действующие между этими поверхностями, препятствуют этому. Оба эти явления и вызывают силы трения качения. Чем тверже поверхности, тем меньше вдавливание и тем меньше трение качения.
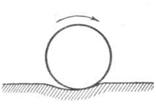
Рис.27. Трение качения
Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется свободной. Задачи решаются с помощью основного закона динамики.
Материальные точки, движение которых ограничено связями, называются несвободными.
Для несвободных точек необходимо определять реакции связей. Эти точки движутся под действием активных сил и ограничивающих движение реакций связей (пассивных сил).
Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождаемости от связей).
2.9.Сила инерции. Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел.
Сила инерции — сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом. Силу инерции называют фиктивной, потому, что нельзя указать тело, со стороны которого она действует. Момент пары сил инерции всегда направлен в противоположную сторону углового ускорения тела.
Рассчитано, что сила инерции равна Fин = | m а|. Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению (движению).
Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).
Даламбер предложил условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становиться уравновешенной, и можно при решении задач динамики использовать уравнение статики.
2.10. Принцип Даламбера: материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии.
Порядок решения задач с использованием принципа Даламбера:
1. Составить расчетную схему.
2. Выбрать систему координат.
3. Выяснить направление и величину ускорения.
4. Условно приложить силу инерции.
5. Составить систему уравнений равновесия.
6. Определить неизвестные величины.
2.11. Работа. Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы».
Работа служит мерой действия силы, работа — скалярная величина.
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения: А = FScosα. Единицы измерения работы: 1 Дж (джоуль)= 1 Н*м; 1 кДж (килоджоуль) = 103 Дж.
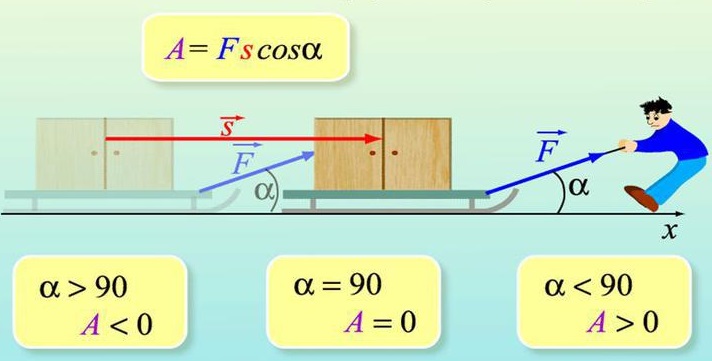
Рис.28. Работа силы
Рассмотрим частные случаи.
Силы, совпадающие с направлением перемещения, называются движущими силами. Направление вектора силы совпадает с направлением перемещения. В этом случае а = 0° (cos α = 1).
Тогда А = FS > 0.
Силы, перпендикулярные направлению перемещения, работы не производят. Сила F перпендикулярна направлению перемещения, а = 90° (cosa = 0); А = 0.
Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления. Сила F направлена в обратную от перемещения S сторону.
В этом случае а — 180° (cos α = —1), следовательно, А = — FS < 0.
Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость. Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
Работа силы тяжести зависит только от изменения высоты и равна произведению модуля силы тяжести на вертикальное перемещение точки:
А(G) = G(hi - h2) = GΔh, где Δh — изменение высоты. При опускании работа положительна, при подъеме отрицательна.
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
2.12. Мощность — работа, выполненная в единицу времени. Характеризует скорость осуществления механической работы (работа за единицу времени). Единица измерения мощности: ватты, киловатты
(1 нм/сек = 1 Дж/сек = 1 Вт).
Мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Работа и мощность при вращении тела. Часто встречаются детали машин, вращающиеся вокруг неподвижных осей. Причиной вращения является приложенный к телу вращающий момент относительно оси, который создается парой сил или силой F, линия действия которой не пересекает ось вращения.
Работа определяется как произведение силы на перемещение или равна произведению момента на угол поворота.
Mощность при вращательном движении тела равна произведению вращающего момента (момента пары) на угловую скорость.
| [Введите цитату из документа или краткое описание интересного события. Надпись можно поместить в любое место документа. Для изменения форматирования надписи, содержащей броские цитаты, используйте вкладку "Средства рисования".] |
2.13. Энергия. КПД. Способность тела при переходе из одного состояния в другое совершать работу называется энергией. Энергия есть общая мера различных форм движения и взаимодействия материи.
Рис.29. КПД механизма
При передаче или преобразовании энергии, а так же при совершении работы происходит потеря энергии. В процессе передачи движения или выполнения работы движущие силы механизмов и машин преодолевают силы сопротивления, которые подразделяются на силы полезного сопротивления и силы вредного сопротивления. Потери на преодоление сил вредного сопротивления имеются во всех механизмах и машинах и вызываются силами трения и силами сопротивления окружающей среды.
Относительное количество энергии, используемой в машине по прямому назначению, характеризуется коэффициентом полезного действия (КПД).
Коэффициент полезного действия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»). η = Wпол/Wcyм. КПД является безразмерной величиной и часто измеряется в процентах.
Существуют две основные формы механической энергии: потенциальная энергия, или энергия, которой обладают тела в состоянии покоя. Кинетическая энергия, или энергия движения, это энергия тела, приобретенная при движении. Эти две энергии могут превращаться друг в друга.
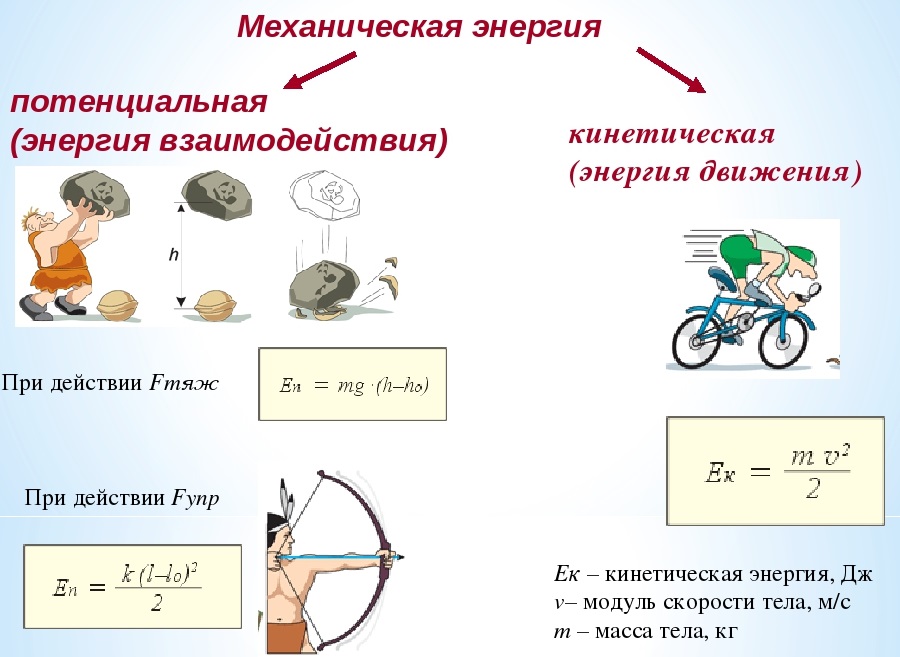
Рис.30. Потенциальная и кинетические энергии
Чаще всего приходится иметь дело с потенциальной энергией сил тяжести. Потенциальной энергией силы тяжести материальной точки или тела в механике называется способность этого тела или точки совершать работу при опускании с некоторой высоты до уровня моря (до какого-то уровня). Потенциальная энергия численно равна работе силы тяжести, произведенной при перемещении с нулевого уровня до заданного положения.
Кинетическая энергия определяется способностью движущегося тела (или точки) совершать работу. Для материальной точки кинетическая энергия численно равна полупроизведению ее массы на квадрат скорости.
Потенциальная и кинетическая энергия измеряются в единицах работы – в Джоулях.
2.14.Контрольная работа по дисциплине
«Теоретическая механика».
Для выполнения контрольной работы необходимо решить свой вариант задачи.
Дано: тело в виде цилиндра (например, бревно, бочка, труба) определенной массы и диаметра (смотри данные в табл. 7,8 и рис. 31) лежит на ровной поверхности. Заданы коэффициенты трения скольжения и коэффициенты трения качения.
Найти: усилие Q при котором цилиндр сдвинется с места, а также определить, как цилиндр будет двигаться: катиться или скользить?
Вариант исходных данных к задаче выбирается по последней и предпоследней цифре зачетной книжки.
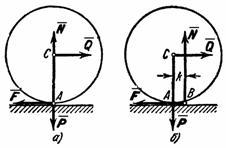
Рис.31. Качение цилиндра по поверхности
Таблица 7.
| Вариант, последняя цифра зачетной книжки | Масса цилиндра, кг | Коэффициент трения скольжения |
| 0 | 100 | 0,6 |
| 1 | 200 | 0,5 |
| 2 | 300 | 0,4 |
| 3 | 400 | 0,3 |
| 4 | 500 | 0,2 |
| 5 | 600 | 0,1 |
| 6 | 700 | 0,09 |
| 7 | 800 | 0,06 |
| 8 | 900 | 0,03 |
| 9 | 1000 | 0,01 |
Таблица 8.
| Вариант, предпоследняя цифра зачетной книжки | Диаметр цилиндра, м | Коэффициент трения качения, мм |
| 0 | 0,5 | 190 |
| 1 | 0,7 | 170 |
| 2 | 0,9 | 150 |
| 3 | 1,2 | 130 |
| 4 | 1,4 | 110 |
| 5 | 1,6 | 90 |
| 6 | 1,8 | 70 |
| 7 | 2,0 | 50 |
| 8 | 2,2 | 30 |
| 9 | 2,4 | 10 |
3.Основы дисциплины «Сопротивление материалов».
Лекция 1. Что изучает дисциплина «Сопротивление материалов». Основные требования к деталям и конструкциям и виды расчетов. Основные гипотезы и допущения. Классификация нагрузок. Расчетные модели. Метод сечений. Внутренние силовые факторы. Напряжения. Напряжения при растяжении и сжатии. Продольные и поперечные деформации. Закон Гука. Перемещение. Механические испытания. Механические характеристики прочности и пластичности. Виды диаграмм растяжения. Предельные и допустимые напряжения. Расчеты на прочность при растяжении и сжатии.
Лекция 2. Основные предпосылки расчетов на сдвиг (срез) и смятие. Закон Гука при сдвиге. Примеры деталей, работающих на срез и смятие. Практические расчеты осей, шпонок, заклепок, сварных швов. Деформации при кручении, гипотезы. Напряжение и деформации при кручении. Распределение напряжений по поперечному сечению. Максимальные напряжения. Расчеты на прочность. Расчеты на жесткость.
Лекция 3. Дифференциальные зависимости при прямом поперечном изгибе. Правила построения и контроля эпюр. Деформации при чистом изгибе. Нормальные напряжения при изгибе. Рациональные сечения при изгибе. Расчет на прочность при изгибе. Понятие о касательных напряжениях при изгибе. Понятие о линейных и угловых перемещениях.
Контрольная работа по дисциплине «Сопротивление материалов».
3.1.Что изучает дисциплина «Сопротивление материалов». Дисциплина «Сопротивление материалов» - это раздел «механики», в котором излагаются методы расчета элементов конструкций на: прочность, жесткость и устойчивость.
Прочность - способность не разрушаться под нагрузкой.
Жесткость - способность незначительно деформироваться под нагрузкой.
Устойчивость - способность сохранять первоначальную форму упругого равновесия.
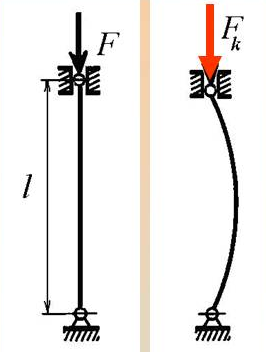
Рис.32. Устойчивость стержня
Дополнительные свойства конструкций: выносливость - способность длительное время выдерживать переменные нагрузки, вязкость - способность воспринимать ударные нагрузки и др.
3.2.Основные требования к деталям и конструкциям. Детали должны быть: прочными, то есть не разрушаться под нагрузкой, жесткими, то есть не деформироваться под нагрузкой, устойчивыми, то есть не терять первоначальную форму упругого равновесия.
3.3.Виды расчетов в сопротивлении материалов. Расчет на прочность обеспечивает неразрушение конструкции. Расчет на жесткость обеспечивает деформации конструкции под нагрузкой в пределах допустимых норм. Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.
Дополнительные расчеты: например, для обеспечения прочности конструкций, работающих при ударных нагрузках (при ковке, штамповке и подобных случаях), проводятся расчеты на удар.
3.4.Основные гипотезы и допущения. Решение задач в сопромате с полным учетом всех свойств реального объекта невозможно. Поэтому принимается ряд допущений и гипотез.
3.4.1.Допущения о свойствах материалов. Материалы однородные - в любой точке материалы имеют одинаковые физико-механические свойства.
Материалы представляют сплошную среду - тело, сплошное и непрерывное до деформации, остается таким же и в процессе деформации, а кристаллическое строение и микроскопические дефекты не учитываются.
Материалы изотропны - механические свойства не зависят от направления нагружения, в любой точке тела и в любом направлении физико-механические свойства материала считаются одинаковыми.
Материалы обладают идеальной упругостью - полностью восстанавливают форму и размеры после снятия нагрузки, т.е. деформации полностью исчезают после прекращения нагрузок.
3.4.2. Допущения о формах элементов конструкции. Все многообразие форм деталей сводятся к четырем видам: брус, пластина, оболочка и массивное тело. Брус (стержень) - тело, длина которого превышает его поперечные размеры. Пластина - тело плоской формы, у которого длина и ширина больше по сравнению с толщиной. Оболочка - тело, ограниченное двумя близко расположенными криволинейными поверхностями. Толщина оболочки мала по сравнению с другими габаритными размерами, радиусами кривизны ее поверхности. Массивное тело (массив) - тело, у которого все размеры одного порядка.
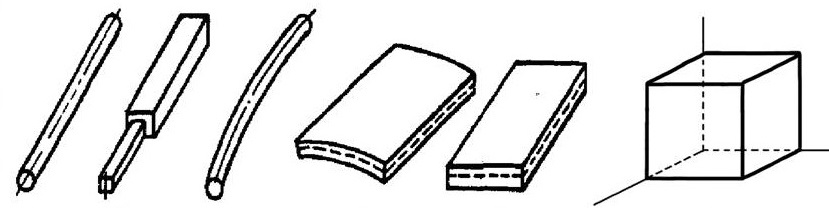
а б в г д е
Рис.33. Формы элементов конструкции:
а,б,в – брус, г – оболочка, д – пластина, е – массивное тело
3.4.3. Допущения о характере деформаций. Деформации, возникающие в деталях под действием внешних сил, очень малы по сравнению с размерами тела. Деформации настолько малы, что не изменяют положения внешних сил, действующих на тело.
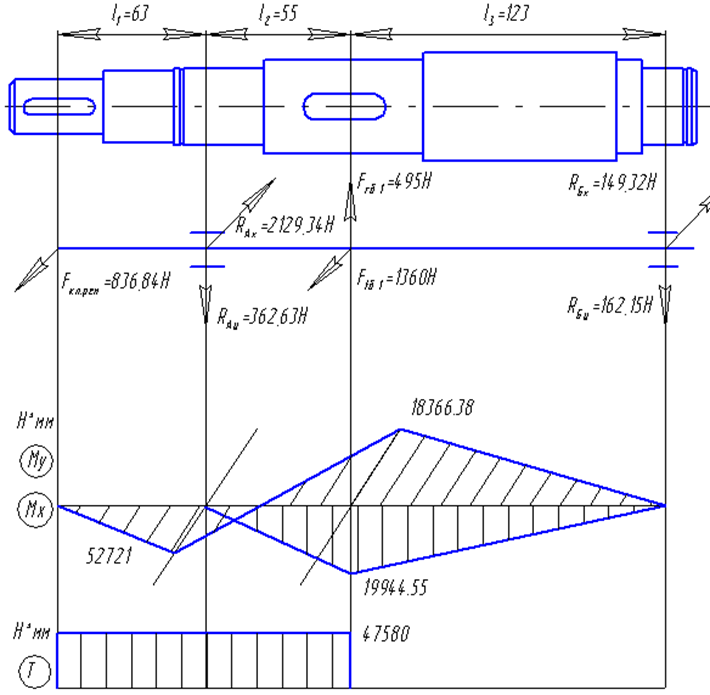
Рис.34. Реальная конструкция вала и его расчетная схема
Перемещения точек деталей прямо пропорциональны действующим нагрузкам. Внешние силы действуют независимо друг от друга (принцип суперпозиции), то есть деформации тела, вызванные действиями нескольких сил, равняются сумме деформаций, вызванных каждой силой в отдельности. Гипотеза плоских сечений: сечение детали плоское до деформирования остается плоским и после деформации. Принцип Сен-Венана: статически эквивалентные системы сил, действующие на малую, по сравнению с общими размерами тела, его часть, при достаточном отдалении от этой части вызывают одинаковые деформации тела. Принцип затвердения: тело, испытывающее деформирование, затвердело и к нему можно применять уравнения статики.
3.4.4.Каждый инженерный расчет состоит из трех этапов:
1. Идеализация объекта (выделяются наиболее существенные особенности реальной конструкции - создается расчетная схема).
2. Анализ расчетной схемы.
3. Обратный переход от расчетной схемы к реальной конструкции и формулирование выводов.
3.5.Классификация нагрузок. Различают внешние и внутренние силы и моменты.
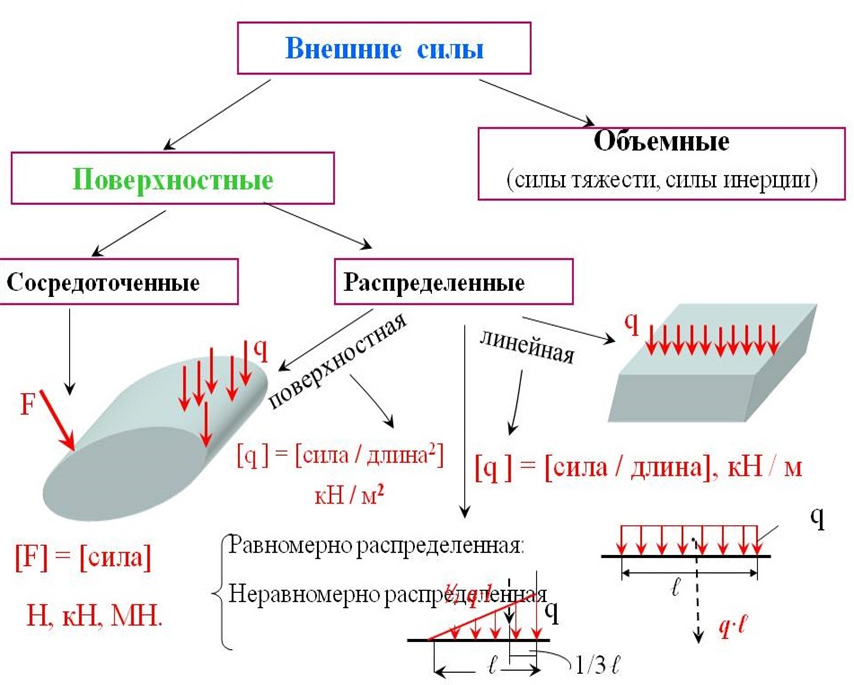
Рис.35. Схематизация внешних сил
3.5.1.Внешние силы - это активные силы и реакции связи. По характеру действия внешние силы делятся на:
статические - прикладывается медленно, возрастая от нуля до конечного значения, и не изменяются,
динамические - изменяют величину или направление за короткий промежуток времени,
динамические внезапные - действуют сразу на полную силу,
ударные - действуют на протяжении короткого времени,
циклические – действуют периодически, например нагрузка на зубья зубчатого колеса.
При нагрузке тел внешними силами тела могут изменять свою форму и размеры. Изменение формы и размеров тела под действием внешних сил называется деформацией .
3.5.2.Деформации бывают: упругие - исчезают после прекращения действия вызвавших их сил, пластичные - не исчезают после прекращения действия вызвавших их сил.
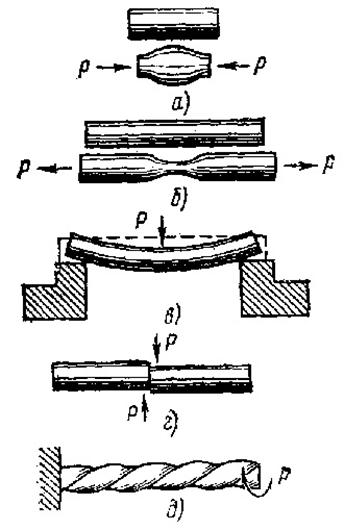
Рис.36. Виды деформаций:
а – сжатие, б – растяжение, в – изгиб, г – сдвиг (срез), д – кручение
В зависимости от характера внешних сил различают следующие виды деформаций:
растяжение-сжатие - состояние сопротивления, которое характеризуется удлинением или укорочением,
сдвиг - смещение двух сопредельных поверхностей относительно друг друга при неизменном расстоянии между ними,
кручение - взаимный поворот поперечных сечений относительно друг друга,
изгиб – состоит в искривлении оси.
Бывают более сложные деформации, которые образуются сочетанием нескольких основных видов деформаций, например – изгиб и кручение.
Линейные деформации связаны с перемещением точек или сечений вдоль прямой линии (растяжение, сжатие).
Угловые деформации связаны с относительным поворотом одного сечения относительно другого (кручение).
3.5.3.Внутренние силы - это силы механического взаимодействия между частичками материала, возникающие в процессе деформирования как реакции материала на внешнюю нагрузку. Можно и так сказать, что внутренние силы – это силы, которые сопротивляются изменению формы и размеров под действием внешних сил.
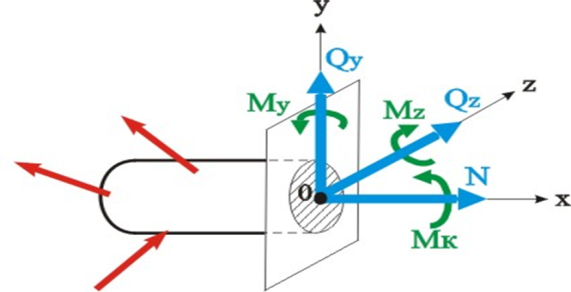
Рис.37. Внутренние силы
3.6.Расчетные модели в сопротивлении материалов. Расчет реального объекта может являться или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов используют расчетные схемы и модели, в которых применяют упрощения, облегчающие расчет.
3.6.1.Расчетная схема (модель) - идеализированная схема, отражающая наиболее существенные особенности реального объекта. В зависимости от постановки задачи и требуемой точности ее решения для одной и той же конструкции может быть предложено несколько расчетных схем.
Одна из целей сопротивления материалов - создать практически приемлемые простые приемы расчета типовых, наиболее часто встречающихся элементов конструкций.
Необходимость перехода от реального объекта к расчетной схеме с целью упрощения расчетов заставляет вводить схематизацию понятий.
Выделяют следующие типы схематизации: физическая схематизация, геометрическая схематизация, силовая схематизация.
3.6.2.Физическая схематизация (модель материала) - все изучаемые тела считают изготовленными из материалов, наделенными идеализированными свойствами. Материал элементов конструкций считают сплошным, однородным, изотропным и линейно упругим.
3.6.3.Геометрическая схематизация (модель формы) - все виды конструктивных элементов, встречающихся в машинах, при всем их разнообразии, можно свести к четырем основным категориям:
массивное тело - это фундаменты сооружений, подпорные стенки, станины станков и т. п.,
брус с прямолинейной осью постоянного сечения, переменного сечения, ступенчатый, и т.д.,
оболочка, различают оболочки цилиндрические, конические, сферические и др. К оболочкам относятся тонкостенные резервуары, котлы, купола зданий, обшивки фюзеляжей, крыльев (и других частей летательных аппаратов), корпуса судов и т. п.,
пластина, толщина пластин, как и оболочек, может быть постоянной или переменной. Пластинами являются плоские днища и крышки резервуаров, перекрытия инженерных сооружений, диски турбомашин.
Тела, имеющие эти основные формы, и являются объектами расчета на прочность, жесткость и устойчивость в сопротивлении материалов.
3.6.4.Схематизацию опор схем реальных устройств можно свести к трем типам.
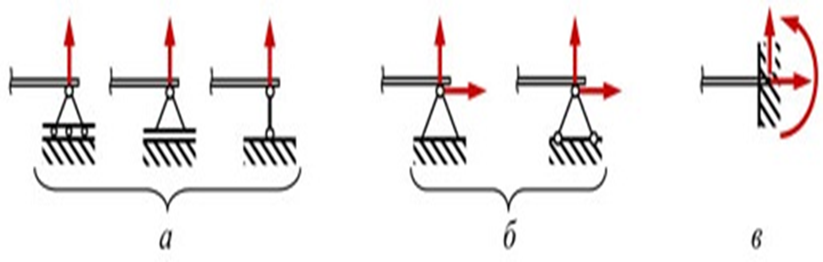
Рис.38. Схематизация опор реальных устройств:
а - шарнирно-подвижная, б - шарнирно-неподвижная, в - заделка
Шарнирно-подвижная опора балки препятствует только вертикальному перемещению конца балки, но ни горизонтальному перемещению, ни повороту. Такая опора при любой нагрузке дает одну реакцию.
Шарнирно-неподвижная опора препятствует вертикальному и горизонтальному перемещениям конца балки, но не препятствует повороту сечения. Дает две реакции: вертикальную и горизонтальную.
Заделка (защемление) препятствует вертикальному и горизонтальному перемещениям конца балки, а также повороту сечения. Дает три реакции: вертикальную и горизонтальную силы и пару сил.
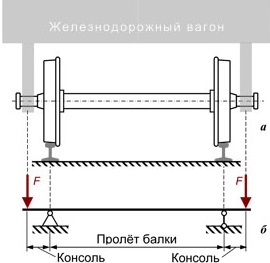
Рис.39. Пример схематизации:
а - реальная конструкция, б - расчетная схема
3.6.5.Силовая схематизация (модель нагружения). В нагруженном теле, находящемся в равновесии, внешние нагрузки стремятся вызвать деформацию тела, а внутренние усилия стремятся сохранить тело как единое целое.
3.7.Метод сечений для определения внутренних сил. Для нахождения и определения внутренних сил применяют метод сечений (РОЗУ), который сводится к следующим операциям:
условно перерезаем тело на две части секущей плоскостью (Р -разрезаем),
отбрасываем одну из частей (О - отбрасываем),
заменяем влияние отброшенной части на оставленную внутренними силами (усилиями) (З - заменяем),
из условий равновесия системы сил, действующих на оставшуюся часть, определяем внутренние силы (У – уравнения равновесия).
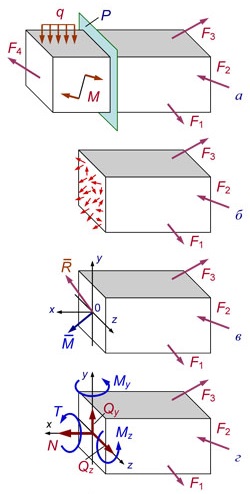
Рис.40. Определение внутренних сил методом сечений
В результате сечения стержня поперечным сечением, разорванные связи между частями заменяются внутренними силами, которые можно свести к главному вектору R и главному моменту М внутренних сил.
При проектировании их на координатные оси получаем шесть компонент внутренний сил: одну продольную (осевую) силу (N), две поперечных силы (Q), один крутящий момент (M) и два изгибающих момента (М). Если известны внешние силы, все шесть компонент внутренних сил могут быть найдены из уравнений равновесия.
3.8.Напряжения. Напряжение в точке тела - это интенсивность внутренней силы, возникающей на бесконечно малой площадке. То есть, напряжение - это внутреннее усилие, приходящееся на единицу площади. Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.
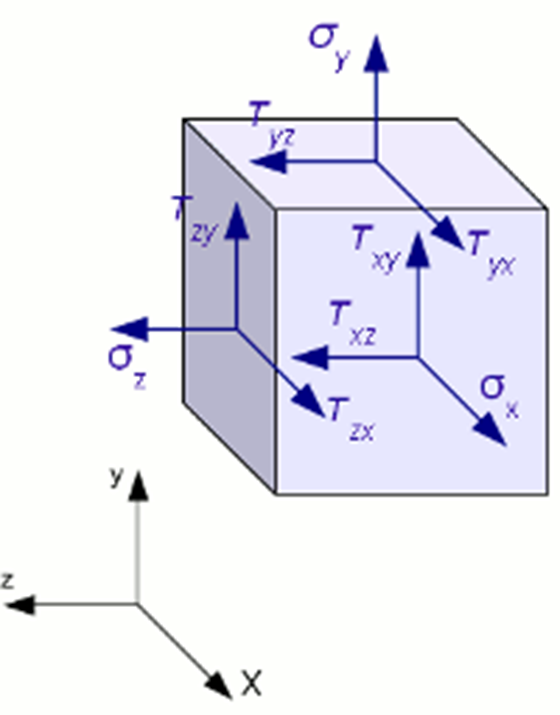
Рис.41. Нормальные и касательные напряжения
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат: нормальное напряжение (σ - сигма), направленное по перпендикуляру к площадке, и касательные напряжения (τ - тау), лежащие в плоскости сечения.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону. Часто используют значения: 1 МПа = 106 Па. В технической системе единицы напряжения измеряются в килограммах силы на миллиметр в квадрате (кгс/мм2).
3.9.Напряжения при растяжении и сжатии. В поперечных сечениях при растяжении-сжатии имеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.
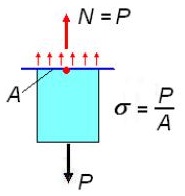
Рис.42. Напряжения в поперечном сечении при растяжении
Знак напряжений зависит от знака внутренней силы на рассматриваемом участке стержня. Для обеспечения необходимой прочности элементов и конструкций напряжения не должны превышать допустимых значений. При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении.
Нормальное напряжение можно рассчитать по формуле:
P N
σ ═ ― ═ ― ,
A A
где:
Р - внешняя сила,
N - внутренняя продольная сила в сечении,
А - площадь поперечного сечения.
Таким образом: величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения, а при сжатии к сечению.
Размерность напряжений: Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа):
1 МПа = 106 Па = 1 Н/мм2.
При определении напряжений брус разбивают на участки, в пределах которых продольные силы не изменяются.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений. Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
Эпюра (чертёж) - это график, который показывает распределение величины нагрузки на объект. Например, для бруса продольная ось симметрии принимается за ось ординат, а по оси абсцисс откладываются значения: вверх (положительные), вниз (отрицательные) значения нагрузок: продольных сил и напряжений. То есть эпюра - это график изменения внутреннего силового фактора по длине бруса. Инженеры-механики чаще используют понятие брус, а инженеры-строители используют понятие стержень, который является частью рам или ферм. Допустимо использовать оба этих понятия.
Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.
Расчет нормальных напряжений при растяжении-сжатии производится по формуле 1. Растяжением - сжатием называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила N. Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в этом сечении.
Продольная сила в любом сечении бруса определяется методом сечений: она равна алгебраической сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось. Если продольная сила по всей длине бруса не постоянна, то строят эпюру «N».
3.9.1.Алгоритм построения эпюр продольных сил:
1. Разбиваем брус на участки, границами которых являются сечения, где приложены внешние силы.
2. В пределах каждого участка применяют метод сечений и определяют продольную силу. При этом если внешняя сила растягивает оставленную часть стержня, т.е. направлена от сечения - продольная сила положительна; если внешняя сила сжимает оставленную часть стержня, т.е. направлена к сечению - продольная сила отрицательна.
3. Откладываем полученные значения по оси абсцисс: вверх от оси ординат - положительное значение, вниз - отрицательное, и строим эпюру продольных сил.
4. Правильность построения эпюр продольных сил определяется следующим образом: в сечениях, где приложена внешняя сила, на эпюре есть «скачки», равные по величине приложенной силе.
Дата: 2019-02-25, просмотров: 567.
