Пример 1. Определить потребное количество заклепок для передачи внешней нагрузки 120 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно: [σ] = 160 МПа; [σсм] = 300 МПа; [τс] = 100 МПа; диаметр заклепок 16 мм.
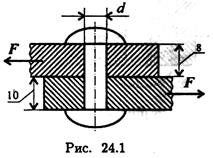
Рис.53. Расчет заклепки на срез и смятие
Решение
1. Определить количество заклепок из расчета на сдвиг.
Условие прочности на сдвиг:
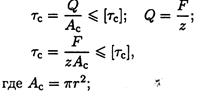
z — количество заклепок.
Откуда:
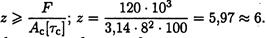
Таким образом, необходимо 6 заклепок.
2. Определить количество заклепок из расчета на смятие. Условие прочности на смятие:
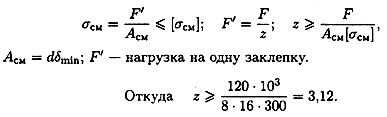
Таким образом, необходимо 4 заклепки.
Для обеспечения прочности на сдвиг (срез) и смятие необходимо 6 заклепок.
Для удобства установки заклепок расстояние между ними и от края листа регламентируется. Шаг в ряду (расстояние между центрами) заклепок 3d; расстояние до края 1,5d. Следовательно, для расположения шести заклепок диаметром 16 мм необходима ширина листа 288мм. Округляем величину до 300мм (b = 300мм).
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями.
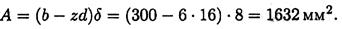
Условие прочности на растяжение:
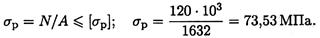
73,53 МПа < 160 МПа. Следовательно, прочность листа обеспечена.
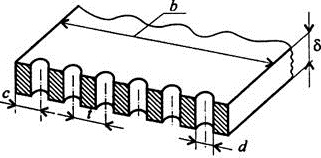
Рис.54. Лист, ослабленный отверстиями под заклепки
Пример 2. Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 60 кН, [τс] = 100 МПа; [σсм] = 240 МПа.
Решение
1.Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (см. рис. 55).
Площадь сдвига каждой заклепки Ас = 2πr2. Площадь смятия боковой поверхности Aсм = dδmin.
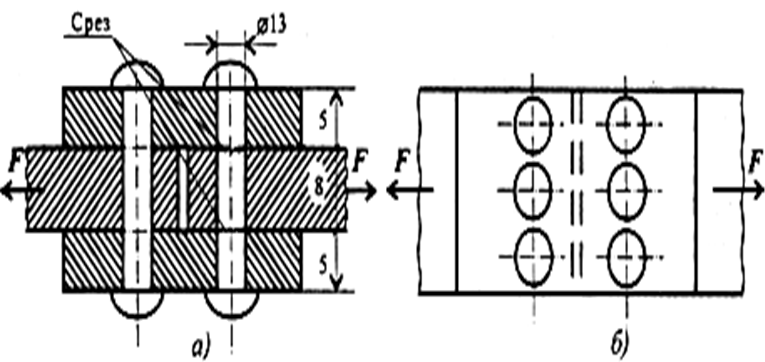
Рис.55. Двухсрезное соединение с заклепками
2. Проверим прочность соединения на сдвиг (срез).
Q = F/z - поперечная сила в поперечном сечении заклепки:
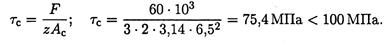
Прочность на сдвиг обеспечена.
3. Проверим прочность соединения на смятие:
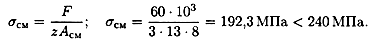
Прочность заклепочного соединения обеспечена.
Пример 3.Определить требуемый диаметр заклепки в нахлесточном соединении (см. рис. 56), если передающаяся сила Q = 120 кН, толщина листов δ = 10 мм. Допускаемые напряжения на срез [τ] = 100 H/мм2, на смятие [σсм] = 200 Н/мм2. Число заклепок в соединении п = 4 (два ряда по две заклепки в каждом).
Решение
Определяем диаметр заклепок. Из условия прочности на срез по сечению аb, учитывая, что заклепки односрезные (т = 1), получаем:
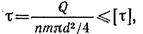
откуда:
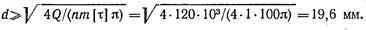
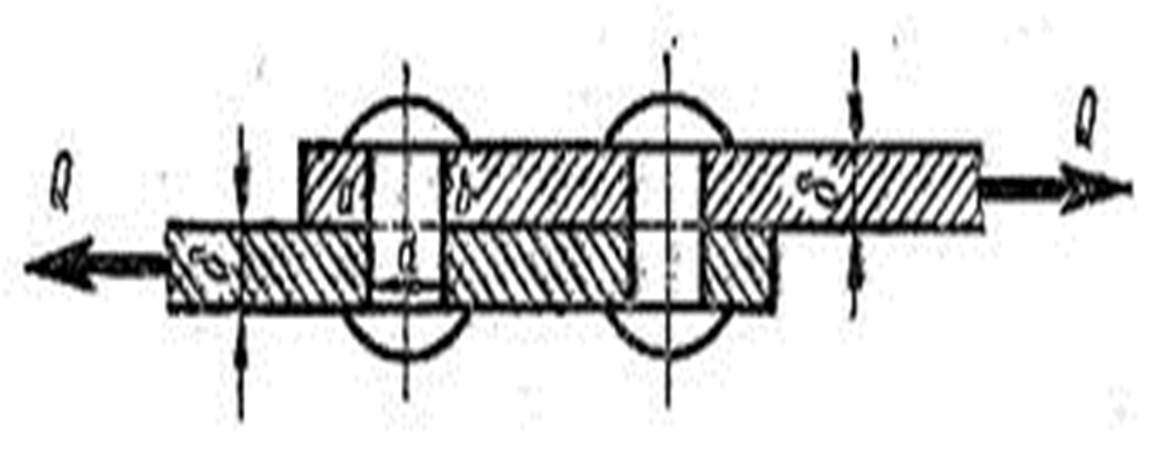
Рис.56. Нахлесточное соединение двух листов с заклепками
Принимаем d = 20 мм.
Из условия прочности соединения на смятие
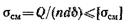
получаем:
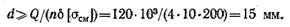
Принимаем большее из найденных значений d = 20 мм.
Пример 4. Определить необходимое количество заклепок диаметром d = 20 мм для нахлесточного соединения двух листов толщиной δ1 = 10 мм и δ2 = 12 мм (см. рис. 56). Сила Q, растягивающая соединение, равна 290 кН. Допускаемые напряжения: на срез [т| = 140 Н/мма, на смятие [σсм] = 300 Н/мм2.
Решение
Из условия прочности на срез необходимое число заклепок при т = 1
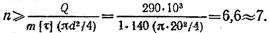
Напряжения смятия будут наибольшими между заклепками и более тонким листом, поэтому в условие прочности на смятие подставляем δmin = 6, и находим
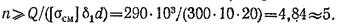
В соединении необходимо поставить 7 заклепок, требуемых по условию прочности на срез.
Пример 5. Два листа с поперечными размерами δ1 = 14 мм, b = 280 мм соединены двусторонними накладками толщиной каждая δ2 = 8 мм (рис.57.). Соединение передает растягивающее усилие Q = 520 кН. Определить число заклепок диаметром d = 20 мм, которое необходимо поставить с каждой стороны стыка. Проверить также прочность листа по опасному сечению, учитывая, что заклепки поставлены по две в ряд (к = 2).
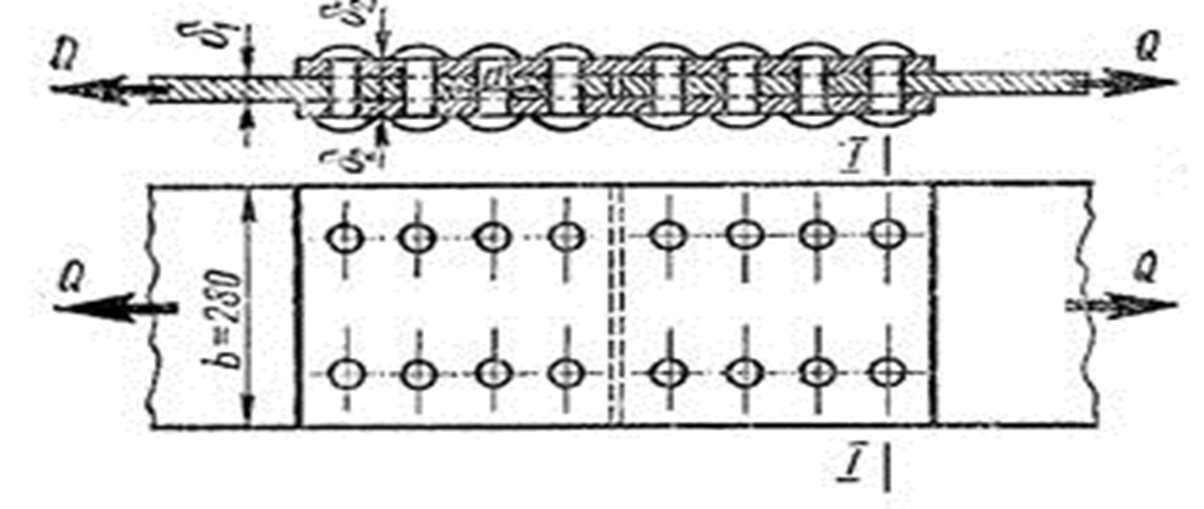
Рис.57. Нахлесточное соединение трех листов с заклепками
Допускаемое напряжение на срез заклепок [τ] = 140Н/мма, на смятие [σсм] = 250 H/мм2, на растяжение листов [σ] = 160 Н/мм2.
Решение
В рассматриваемом соединении заклепки работают как двухсрезные т = 2, т. е. каждая заклепка испытывает деформацию среза по двум поперечным сечениям.
Из условия прочности на срез:
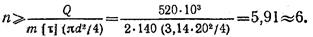
Из условия прочности на смятие, учитывая, что минимальная площадь смятия соответствует δmin = δ1 < 2δ2, получаем:
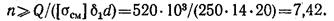
Принимаем п = 8.
В данном случае требуемое количество заклепок из условия прочности на смятие оказалось большим, чем из условия прочности на срез.
Проверяем прочность листа в сечении I — I
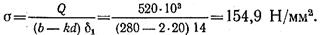
Таким образом, расчетное напряжение в листе меньше допускаемого.
Пример 6. Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 60 кН, допускаемое напряжение металла шва на сдвиг 80 МПа.
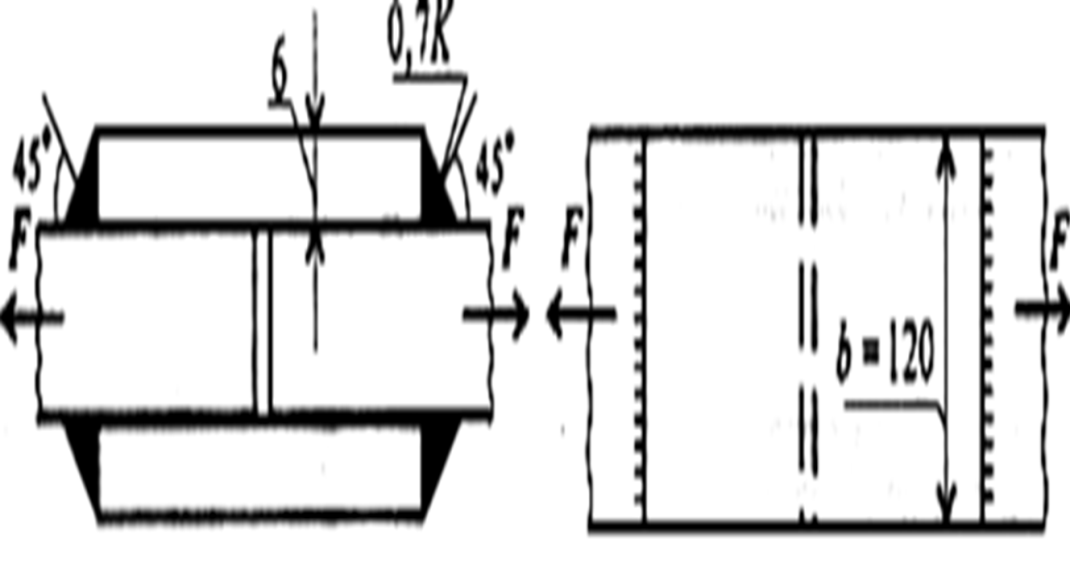
Рис.58. Схема сварного соединения
Решение
1. Нагрузка передается последовательно через два шва слева, а далее - два шва справа. Разрушение угловых швов происходит по площадкам, расположенным под углом 45° к поверхности соединяемых листов.
2. Проверим прочность сварного соединения на срез. Двухсторонний угловой шов можно рассчитать по формуле:
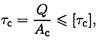
где:
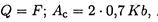
Ас - расчетная площадь среза шва,
К - катет шва, равен толщине накладки,
b - длина шва.
Следовательно,
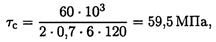
59,5 МПа < 80МПа. Расчетное напряжение меньше допускаемого, прочность обеспечена.
3.27.Деформации при кручении. Кручением называют такой вид деформации, когда в поперечных сечениях бруса возникает единственный силовой фактор – крутящий момент.
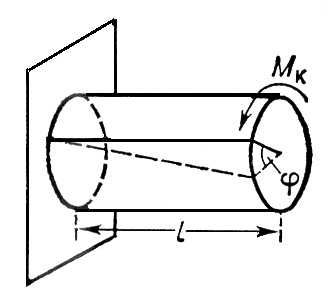
Рис.59. Кручение бруса
Кручение круглого бруса происходит при нагружении моментами (парами сил) в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ, называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения).
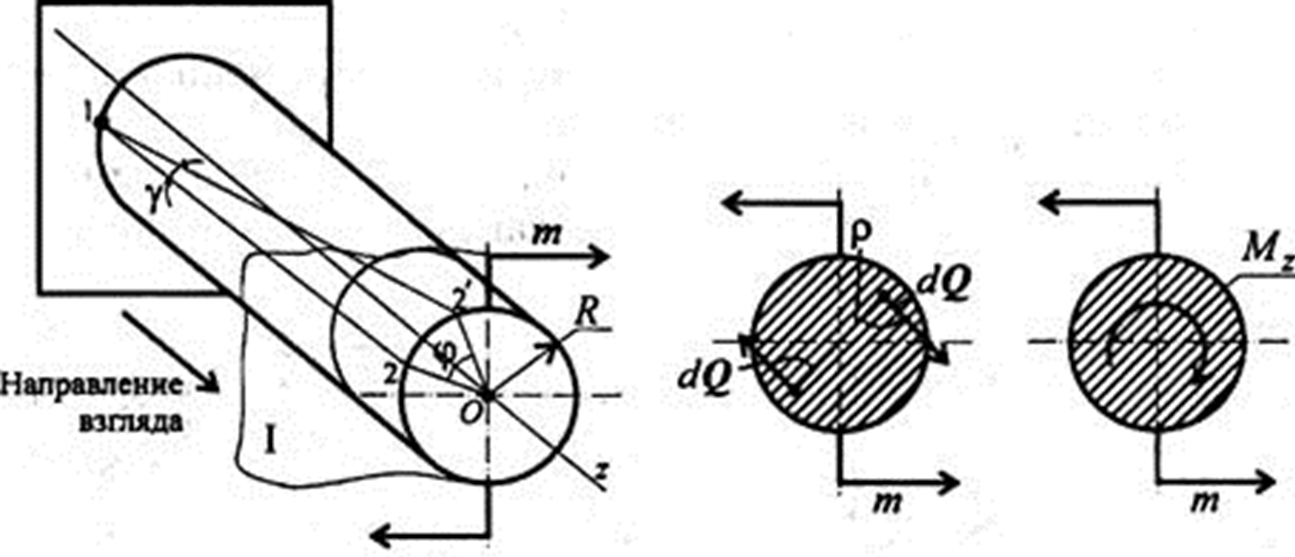
Рис.60. Угол поворота сечения бруса при кручении
3.28.Гипотезы при кручении:
1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).
3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных сечений не меняются.
Рис.61. Пример работы торсиона
Дата: 2019-02-25, просмотров: 632.