В поперечных сечениях бруса нормальные напряжения (направленные вдоль оси) отсутствуют, а возникают только касательные напряжения.
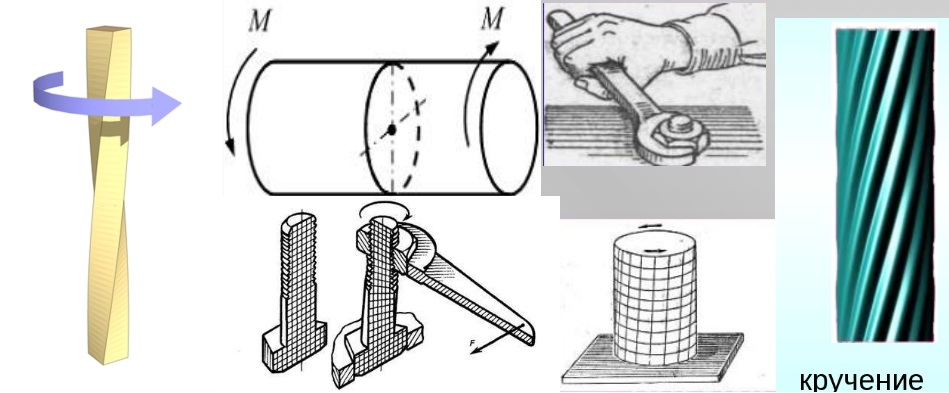
Рис.62. Примеры кручение бруса
Закон Гука при кручении:
τ = Gφ0r,
где:
τ - касательное напряжение при кручении бруса, (Мпа),
G - модуль упругости второго рода, (Мпа), (справочные данные),
φ0 ═ φ / L - относительный угол закручивания,
r - радиус бруса.
3.30.Максимальные напряжения при кручении.
Можно сделать вывод, что для центрального волокна бруса (т. е. расположенного в центре сечения) касательные напряжения равны нулю: так как r = 0, то τ = 0.
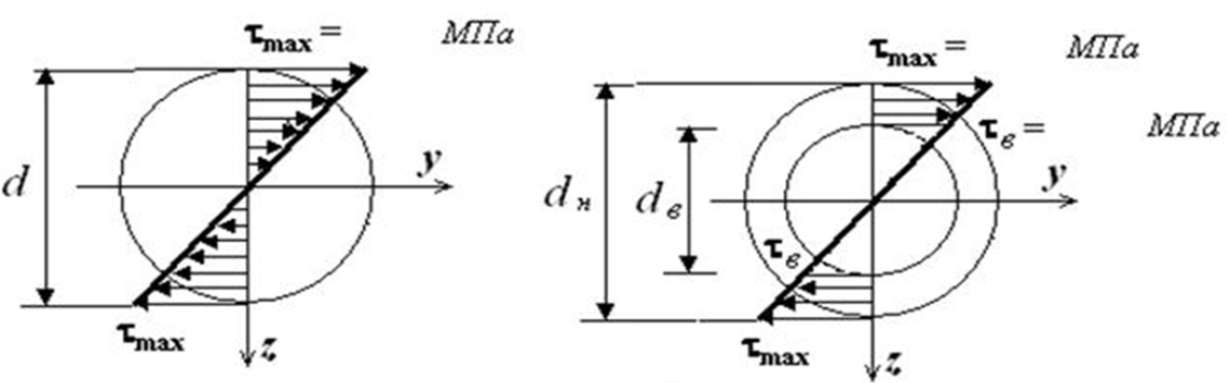
Рис.63. Распределение касательных напряжений по сечению
Полнотелого и пустотелого бруса
Максимального значения касательные напряжения достигают на внешней поверхности бруса, так как r = R, то τ = τmax .
В круглых валах наиболее напряженными являются внешние слои, а внутренние почти не испытывают нагрузки. По этой причине многие валы изготавливаются пустотелыми.
Расчет валов на прочность при кручении.
τmax = Мкр / Wr ≤ [τ],
где:
Wкруч - момент сопротивления сечения кручению (полярный момент сопротивления).
Для круглого вала: Wкруч = πd3 / 16.
Для вала, имеющего кольцевое сечение (труба):
Wкруч = π(d4 мах- d4м in ) / 16D,
Для справки: для стали [τ]=0,55....0,6[σр],
для чугуна [τ] = 1,0....1,2 [σр].
Расчет валов на жесткость при кручении.
За меру жесткости вала принимается: относительный угол закручивания, равный:
φ0 = φ / L ,
Условие жесткости вала выражается формулой:
φ0 = Мкр 180о / Јр Ԍ π ≤ [φ],
где:
Мкр - крутящий момент, (нм),
Јр - полярный момент инерции сечения вала, (м4),
Ԍ - модуль упругости второго рода, Ԍ ≈ 0,4 Е, (н/м2),
π = 3,14
[φ] = (0,3-1,0) град/м, - допустимый угол закручивания.
Дифференциальные зависимости при прямом поперечном
изгибе (теорема Журавского Д.И.)
Изгибающий момент, поперечная сила и интенсивность распределенной нагрузки связаны следующими зависимостями, которые в сопротивлении материалов называются - зависимостями Д.И. Журавского:
1.Интенсивность равномерно распределенной нагрузки равна производной от поперечной силы по длине балки.
2.Поперечная сила равна первой производной от изгибающего момента по длине балки.
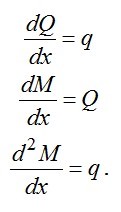
Рис.64. Дифференциальные зависимости при прямом поперечном изгибе
3.34.Правила построения и контроля эпюр. На основании дифференциальных зависимостей можно сделать ряд выводов:
1.Если на некотором участке балки отсутствует распределенная нагрузка (q=0), то эпюра Q - прямая, параллельная к оси абсцисс (Q=const), а эпюра М на этом участке наклонная прямая.
2.Если на некотором участке есть равномерно распределенная нагрузка, то эпюра Q - наклонная прямая, а эпюра М – парабола.
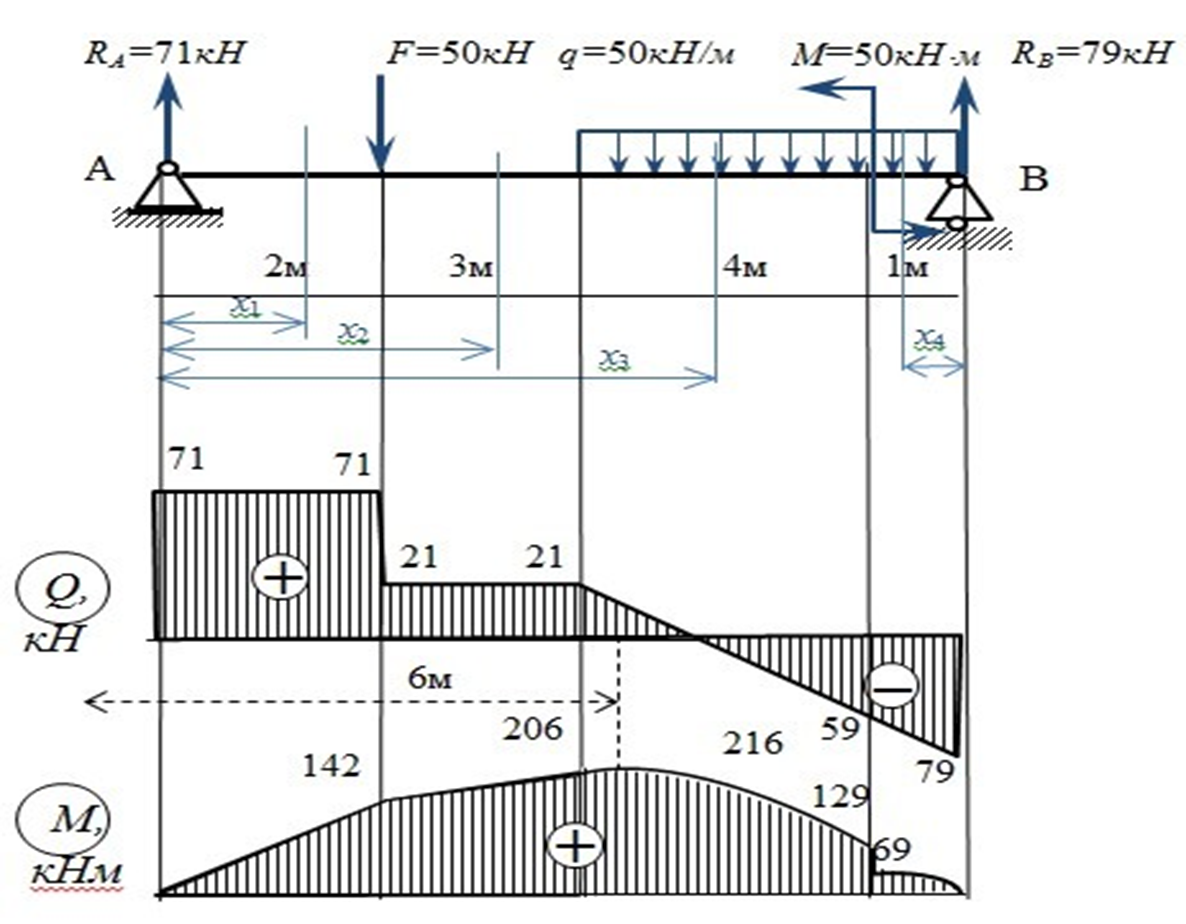
Рис.65. Построение и контроль эпюр
3.Если на некотором участке балки: Q >0, то изгибающий момент возрастает, Q <0,то изгибающий момент убывает, Q = 0, то изгибающий момент постоянный.
4.Если поперечная сила, изменяясь по линейному закону, проходит через нулевое значение, то в соответствующем сечении изгибающий момент будет иметь экстремум.
5.Под сосредоточенной силой на эпюре Q образуется «скачок» на величину приложенной силы, а на эпюру М - резкое изменение угла наклона соседних участков.
6.В сечении, где приложена пара сил, эпюра М будет иметь «скачок» на величину момента пары. На эпюре Q это не отразиться.
7.Если равномерно распределенная нагрузка направлена вниз (вторая производная, которая характеризует кривизну линии), эпюра М обращена выпуклостью вверх, навстречу нагрузке.
3.35.Деформации при чистом изгибе. Чистым называется изгиб, при котором изгибающий момент является единственным внутренним силовым фактором, возникающем в поперечном сечении балки.
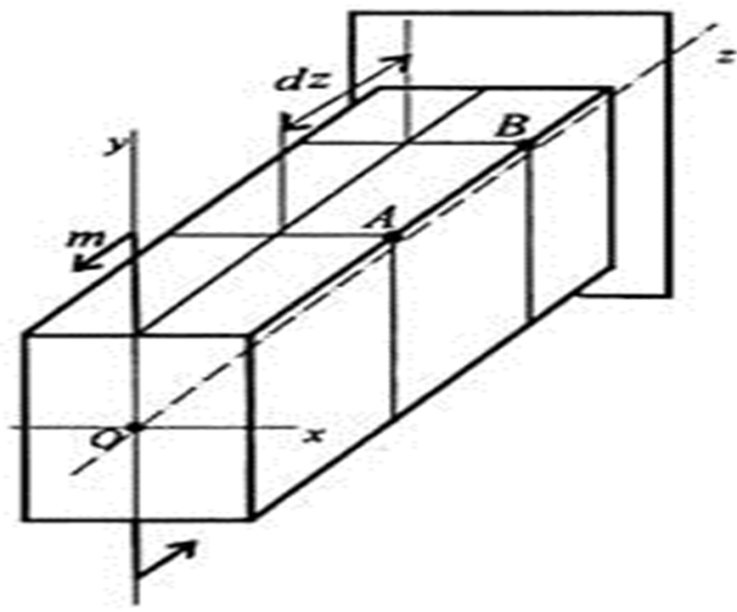
Рис.66. Чистый изгиб балки
Сечения бруса, плоские и перпендикулярные продольной оси, после деформации остаются плоскими и перпендикулярными продольной оси. Продольные волокна не давят друг на друга, поэтому слои испытывают простое растяжение или сжатие. Действуют только нормальные напряжения. Поперечные размеры сечений не меняются.

Рис.67. Деформации балки при чистом изгибе
Продольная ось бруса после деформации изгиба искривляется и образует дугу окружности радиуса ρ. Материал подчиняется закону Гука.
Слои бруса, расположенные ниже продольной оси, сжаты, расположенные выше оси - растянуты. Так как деформации по высоте сечения меняются непрерывно, имеется слой, в котором нормальные напряжения σ равны нулю; такой слой называют нейтральным слоем. Нейтральный слой проходит через центр тяжести сечения; ρ — радиус кривизны нейтрального слоя.
3.36.Нормальные напряжения при чистом изгибе балки
Так как при чистом изгибе деформации волокон балки пропорциональны их расстоянию от нейтрального слоя, то нормальные напряжения изменяются по высоте сечения линейно:
Mx
σ ═ ― · y ,
Jx
где:
σ – нормальное напряжение (растяжения или сжатия),
Mx – изгибающий момент,
Jx – момент инерции сечения балки,
y – координата сечения балки по высоте от нейтрального слоя.
Изгибающий момент «Mx» и координату «y» удобнее всего брать по абсолютному значению, а знак напряжения устанавливать исходя из характера деформирования балки (при растяжении – плюс, при сжатии – минус), т.е. по эпюре «М», ординаты которой откладывают со стороны растянутых волокон.
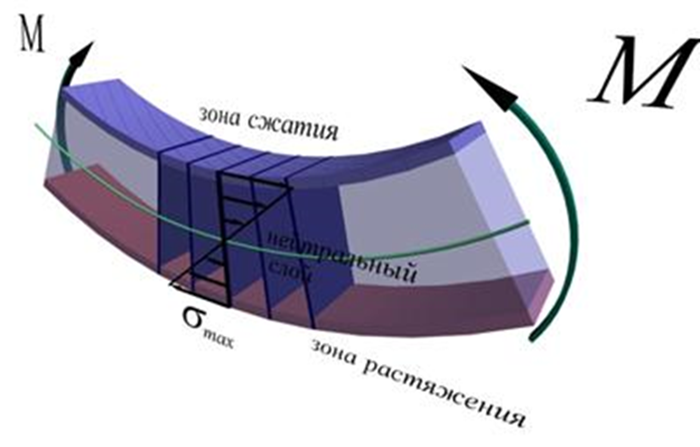
Рис.68. Зона максимальных напряжений при чистом изгибе балки
Следовательно, чем больше координата «y», тем значения напряжений больше. Максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии.
3.37.Рациональные сечения при чистом изгибе балки. Чтобы получить более рациональное сечение, необходимо большую часть материала сечения переместить в зоны, максимально удаленные от нейтральной оси, то есть в те зоны, в которых напряжения максимальны.

Рис.69. Рациональное сечение для пластичного материала балки
при чистом изгибе
Для пластичного материала рациональное сечение будет в форме симметричного двутавра. К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение.
Для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие.
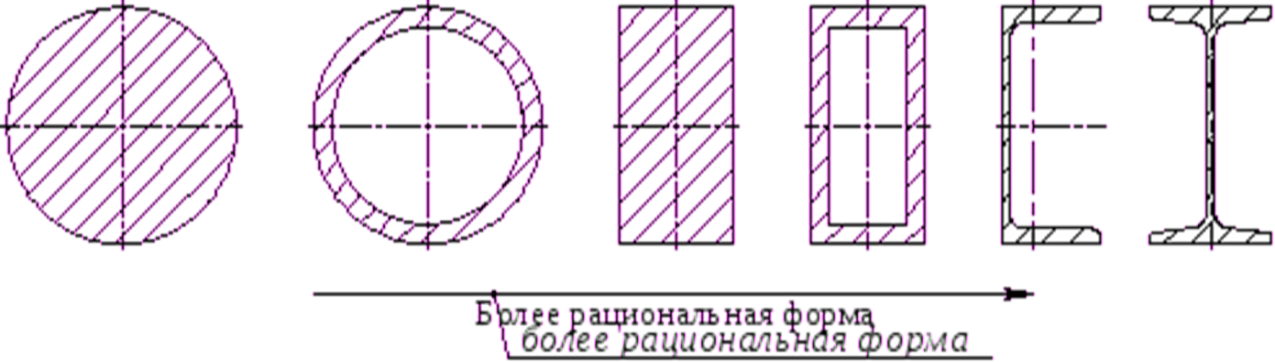
Рис.70. Рациональные сечения балок при чистом изгибе
Вывод: сечения круглые, прямоугольные и ромбовидные нерациональны при чистом изгибе балок.
3.38.Расчет на прочность при изгибе. Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое:
σmax = Мxmax / W ≤ [σ] ,
где:
σmax – максимальное нормальное напряжение в опасном сечении,
Мxmax – максимальный изгибающий момент,
W – момент сопротивления изгибу балки,
[σ] – допускаемое напряжение.
Формула читается так: нормальное напряжение в опасном сечении не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом. Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньшие напряжения возникают в сечении бруса.
Ниже приведены формулы для определения моментов сопротивления изгибу для наиболее часто встречающихся сечений:
1.Прямоугольное сечение размером b x h (ширина и высота сечения): Wпрямоугольное = bh2 / 6 .
2.Круглое сечение диаметром d: Wкруглое = π d3 / 32 ≈ 0,1d3.
3.Кольцо размером D x d: Wкольца = ≈ 0,1 (D4 – d4) / D.
3.39.Понятие о касательных напряжениях при поперечном изгибе. Часто, в поперечном сечении балки наряду с изгибающим моментом возникает также и поперечная сила. Такой изгиб называют поперечным.
При поперечном изгибе в балке возникают не только нормальные, но и касательные напряжения. Последние усложняю картину деформирования, приводя к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений. Однако тщательные исследования показывают, что искажения, вносимые касательными напряжениями, незначительно влияют на нормальные напряжения. Таким образом, при определении нормальных напряжений в случае поперечного изгиба вполне применима теория чистого изгиба. Касательные напряжения в расчетах на прочность, как правило, не учитываются. Большинство балок в конструкциях рассчитывается только по нормальным напряжениям.
Только три вида балок проверяют по касательным напряжениям:
- деревянные балки, т. к. древесина плохо работает на скалывание,
- узкие балки (например, двутавровые), поскольку максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя,
- короткие балки, так как при относительно небольшом изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.
Формула для расчета касательных напряжений для балки квадратного сечения была получена в 1855 году русским инженером Журавским Дмитрием Ивановичем.

Рис.71. Русский инженер-мостостроитель Журавский Д.И.
Наибольшее значение касательного напряжения достигается на нейтральной оси балки. Таким образом, максимальные нормальные напряжения в сечении не совпадают с максимальными касательными.
Журавский Д.И. предложил для длинных балок расчет проводить только по нормальным напряжениям, т. к. касательные здесь незначительны.

Рис.72. Применение формулы Журавского Д.И. при строительстве
Дата: 2019-02-25, просмотров: 816.