1. Разбиваем брус на участки, границами которых являются точки приложения внешних сил и сечения, где меняется площадь.
2. На каждом участке вычисляем нормальные напряжения.
3. Строим эпюру нормальных напряжений, по которой определяем
опасное сечение. При растяжении - сжатии опасным является
сечение, в котором величина нормальных напряжений наибольшая.
Следует помнить, что при растяжении длина детали увеличивается, а
сечение уменьшается; при сжатии - наоборот.
3.9.3.Алгоритм решения задач на построение эпюр продольных сил и нормальных напряжений:
1. Разбить нулевую линию (ось симметрии бруса, стержня) на участки для построения эпюры продольных сил. Границы участков провести в сечениях, где приложены внешние силы.
2. На каждом участке вычислить продольную силу методом сечений.
3. Отложить полученные значения по оси абсцисс и построить эпюру продольных сил. Правильность контролируется так: в сечениях, где к стержню приложены внешние силы, на эпюре продольных сил есть «скачки», численно равные этим силам.
4. Разбить нулевую линию на участки для построения эпюры нормальных напряжений. Границами участков являются сечения, в которых меняется площадь и приложены внешние силы.
5. На каждом участке вычислить нормальное напряжение.
6. Отложить полученные значения по оси абсцисс: (растяжение - плюс, сжатие - минус) и построить эпюру нормальных напряжений. По эпюре определить опасное сечение детали. Опасными являются сечения участка, на котором нормальные напряжения наибольшие.
3.9.4.Методические рекомендации по устранению наиболее часто встречающихся ошибок при построении эпюр:
1.Следует помнить, что на эпюре продольных сил границы участков
проходят в точках приложения внешних сил, а на эпюре нормальных
напряжений - в точках приложения внешних сил и в сечениях, где
меняется площадь стержня.
2.Чтобы правильно подставить значения в формулу нормальных
напряжений, нужно с участка эпюры напряжений, для которого ведется расчет, подняться на эпюру нормальных сил и посмотреть, каково значение продольной силы именно на этом участке. Затем подняться на чертеж детали посмотреть, какова площадь сечения стержня именно на этом участке.
Пример расчета. Рассмотрим брус, нагруженный внешними силами: 3F и 2F вдоль оси. Обнаруживаем три участка нагружения и определяем величины продольных сил.
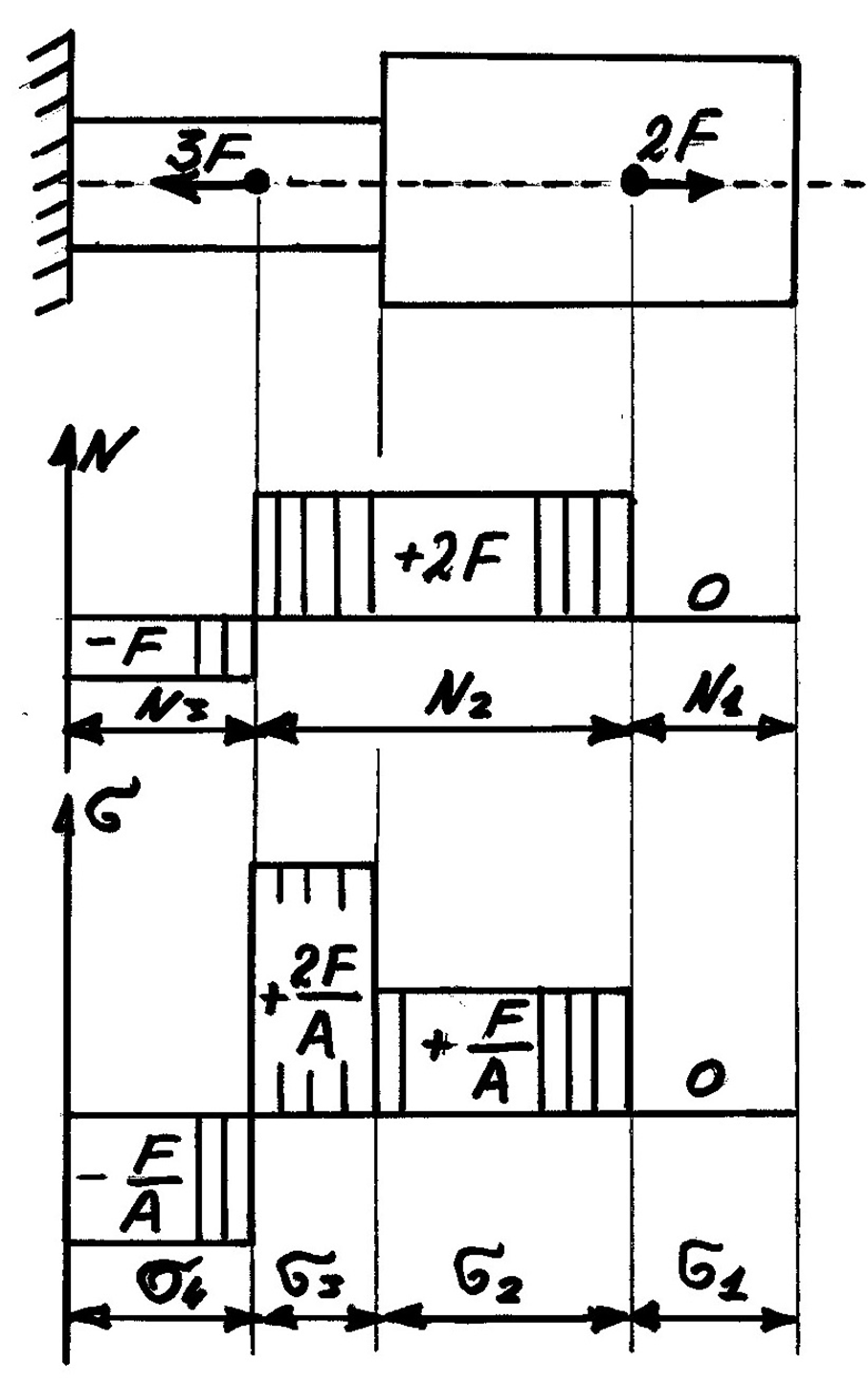
Рис.43. Эпюры продольных сил и напряжений
Границы (3-ех) участков продольных сил N соответствуют границам приложенных внешних сил F.
Участок 1: N1 = 0. Внутренние продольные силы равны нулю.
Участок 2: N2 = 2F. Продольная сила на участке положительна.
Участок 3: N3 = 2F-3F= -F. Продольная сила на участке отрицательна.
Брус - ступенчатый. Напряжения (нормальные) определяем по формуле 1.
Границы (4-ех) участков напряжений соответствуют границам: приложенных внешних сил F и сечений бруса, где меняется его площадь.
Участок 1: N1 = 0, площадь равна 2A.
Участок 2: N2 = 2F, площадь равна 2А.
Участок 3: N3 = 2F, площадь равна А.
Участок 4: N3 = 2F-3F = -F, площадь равна А.
Тогда значения и знаки напряжений равны соответственно:
N1 0
σ 1 ═ ― ═ ― ═ 0,
A 2A
N2 2F F
σ 2 ═ ― ═ ― ═ ― ═ +,
A 2A A
N 3 2 F
σ3 ═ ― ═ ― ═ +,
A A
N 4 - F
σ4 ═ ― ═ ― ═ ̶ ,
A A
По полученным данным строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр выбираются исходя из удобства построения.
3.10.Продольные и поперечные деформации. Пусть в результате деформации первоначальная длина стержня L станет равной L1. Изменение длины:
∆ L ═ L1 ̶ L,
называется абсолютным удлинением стержня.
Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением или продольной деформацией .
Продольная деформация – это безразмерная величина. Формула для определения продольной деформации:
∆ L
ε ═ ―
L
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.
Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются.
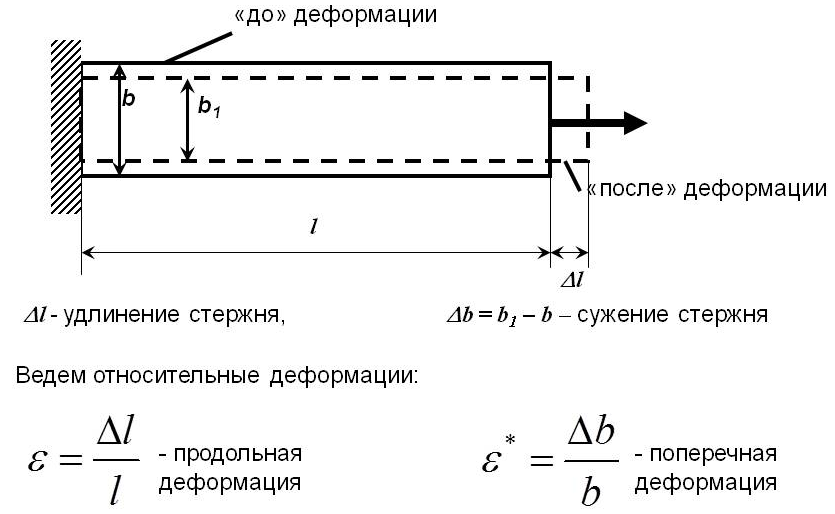
Рис.44. Деформации: продольная и поперечная
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной и называется коэффициентом Пуассона:
έ
μ ═ ―
ε
где:
έ - поперечная деформация,
ε – продольная деформация.
Для различных материалов коэффициент Пуассона изменяется в пределах: 0 ≤ μ ≤ 0,5. Например, для пробки μ ═ 0, для стали μ ═ 0,3. Для каучука μ ═ 0,5.
3.11.Закон Гука: «Каково удлинение, такова и сила»:
σ ═ ε·E ,
где:
E - модуль продольной упругости (модуль Юнга), E = 2·105 Мпа.

Рис.45. Закон Гука
Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения.
Из закона Гука видно, что модуль продольной упругости характеризует жесткость материала при растяжении (сжатии).
3.12.Перемещение - изменение положения точки тела в пространстве вследствие изменения его формы и размеров под действием нагрузки. Перемещения могут быть линейные и угловые. Не путать с деформацией - это изменение формы и размеров тела. Деформация также может быть линейной и угловой.
В частных случаях, например при растяжении и сжатии деформация и перемещение могут совпадать, но в общем случае - это разные вещи.
Например, представим себе канат, прикрепленный к потолку. По канату на некоторую высоту поднялся человек. Очевидно, что под действием веса человека деформируется (растягивается) только верхняя часть каната, заключенная между потолком и местом, где находится человек. Нижняя часть каната не деформируется, а перемещается как твердое тело. Следовательно, не всегда перемещения сечений какого-то участка стержня непосредственно связаны с его деформацией.
3.13.Механические испытания. Механические характеристики материала определяются в результате испытания образца на специальных прессах. При испытании образца автоматически вычерчивает график зависимости между нагрузкой (F) и абсолютным удлинением (∆ L). График называется диаграммой растяжения или диаграмма Бернулли. Эта диаграмма характеризует поведение данного образца, но не материала, из которого он сделан.
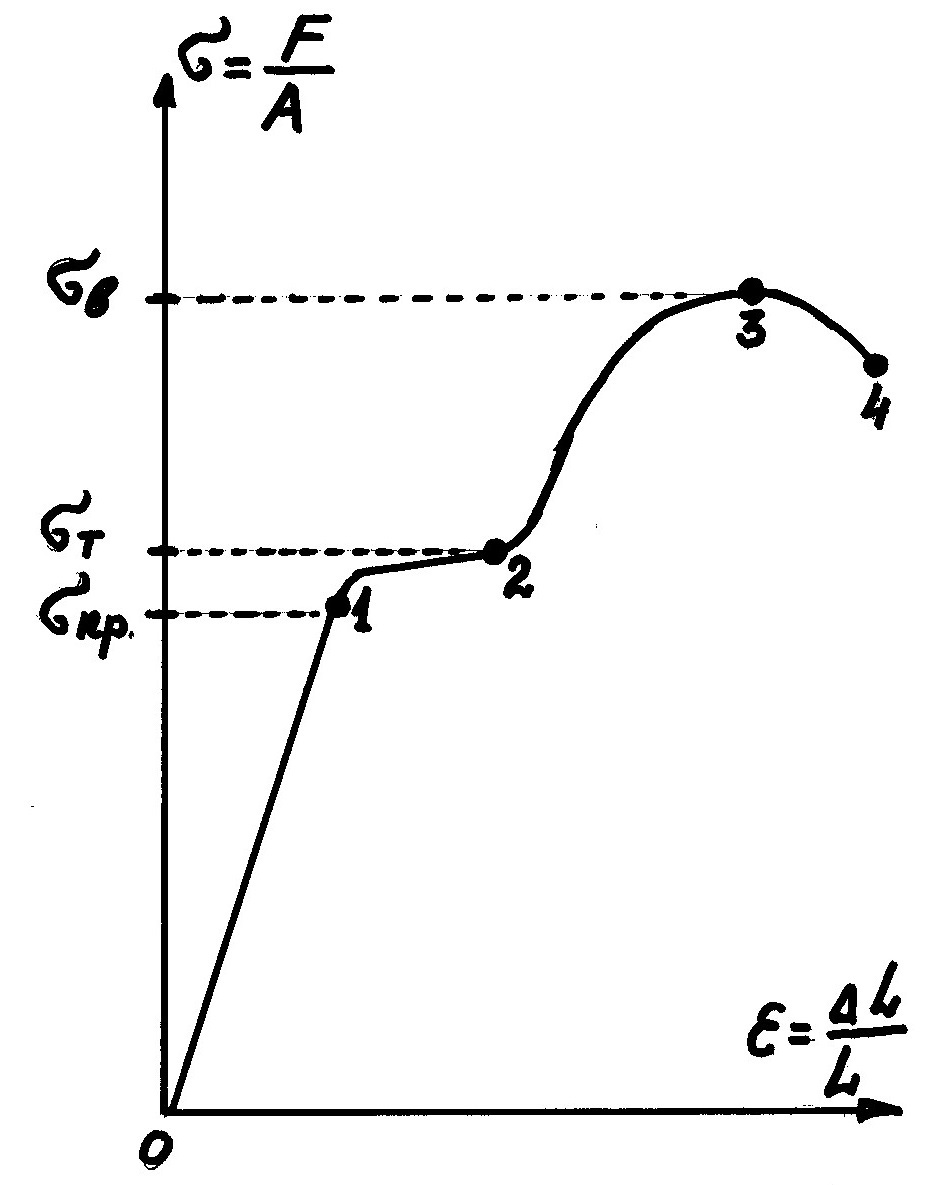
Рис.46. Диаграмма растяжения для малоуглеродистой стали марки Ст.3
Судить о механических свойствах материала, исключая особенности формы и размеров образца, позволяет диаграмма растяжения, представляемая в координатах σ – ε. Здесь σ – условное напряжение; ε – относительное удлинение, А0 – начальная площадь поперечного сечения образца; L0 – начальная длина образца.
Диаграмма растяжения малоуглеродистой стали имеет несколько характерных участков: 01 – участок упругих деформаций; 12 – площадка текучести; 23 – участок упрочнения; 34 – участок образования шейки и разрушения.
Диаграммы растяжения большинства конструкционных металлов: легированных и углеродистых сталей в закаленном и нормализованном состоянии, цветных сплавов, полимеров и других материалов площадки текучести не имеют.
По результатам испытаний определяют характеристики прочности и пластичности.
Дата: 2019-02-25, просмотров: 605.