Погрешности механической обработки и
Законы их распределения
Выделяют три вида погрешностей обработки деталей: погрешности размера, погрешности формы и погрешности взаимного расположения поверхностей и осей детали. При механической обработке деталей на металлорежущих станках источниками этих погрешностей являются станок, приспособление, инструмент и сама обрабатываемая заготовка (сокращенно система СПИЗ).
В зависимости от причин, вызывающих погрешности обработки деталей, выделяют случайные погрешности и систематические. В свою очередь, систематические погрешности подразделяются на постоянные погрешности и закономерно изменяющиеся во времени, т. е. функциональные. Таким образом, все погрешности механической обработки по причинам их образования классифицируют на три основных вида: постоянные, функциональные и случайные.
Требуемая точность обработки в условиях серийного и массового производств обычно обеспечивается настроенным на размер станком. При работе на настроенных станках величина тех или иных погрешностей обработки практически не зависит от оператора, обслуживающего станок. Поэтому в этом случае можно дать следующие определения основным видам погрешностей обработки.
Постоянными называются такие погрешности, которые сохраняют свое значение при обработке каждой новой детали.
Функциональными называются такие погрешности, величина которых закономерно изменяется при обработке каждой новой детали.
Случайными называются такие погрешности, величина которых при обработке каждой новой детали может принять любое численное значение (в определенных пределах), заранее нам неизвестное.
Причин возникновения погрешностей обработки много, но для каждого вида погрешностей можно установить главные, или доминирующие причины.
Постоянныепогрешности обработки возникают вследствие неточности настройки режущего инструмента на размер, неточности изготовления станка, приспособления и мерного режущего инструмента. Погрешности в изготовлении станка, приспособления и режущего инструмента целиком переносятся и на обрабатываемую деталь. Поэтому в зависимости от вида обрабатываемой поверхности и изучаемого параметра точности обработки устанавливается и доминирующая причина постоянных погрешностей. Например, при обработке наружных и внутренних поверхностей резцом или фрезой доминирующей причиной постоянных погрешностей обработки будет неточность установки режущего инструмента на размер; при обработке мерным инструментом (разверткой, зенкером, протяжкой и т. п.) основной причиной постоянных погрешностей будет неточность изготовления режущего инструмента; при нарезании резьбы на токарно-винторезном станке основной причиной постоянной погрешности шага нарезаемой резьбы будет неточность шага ходового винта станка и т. д.
Для погрешностей формы и взаимного расположения поверхностей основными причинами постоянных погрешностей будут являться геометрические неточности станка.
Функциональные погрешности. Главными причинами возникновения функциональных погрешностей обработки являются размерный износ режущего инструмента и его температурные деформации от нагрева в процессе резания, а также температурные деформации станка и температурные деформации обрабатываемой детали. Все эти погрешности являются функцией времени работы станка и режущего инструмента. Однако температурные деформации станка носят временный характер. По истечении определенного времени работы его температура стабилизируется и деформация частей станка прекращается, а погрешность, возникающая по этой причине, превращается в постоянную.
При работе на настроенных станках или при работе мерным режущим инструментом размерный износ систематически изменяет размер каждой новой детали на удвоенную величину износа инструмента при выполнении диаметральных размеров или только на величину износа при выполнении размеров длин. Исследованиями установлено, что размерный износ u режущих инструментов протекает во времени τ по закону, выражаемому кривой 1, показанной на рисунке 1. Эта кривая имеет три участка. Первый участок (от 0 до τн) характеризует изменение износа инструмента в период его приработки. Это участок начального износа инструмента. Второй участок (от τн до τк) характеризует нормальный износ инструмента и третий участок (от τк до конца кривой) - катастрофический износ, при котором наступает быстрое разрушение инструмента.
Если работа производится предварительно доведенным инструментом, размерный износ будет изменяться во времени по закону прямой (см. рисунок 1, линия 2). При этом период стойкости инструмента увеличится, так как доводка инструмента повышает его износостойкость в 1,5 и более раз.
Размерный износ режущего инструмента и интенсивность износа зависят от материала режущего инструмента и материала обрабатываемой детали, от режима резания и геометрии инструмента. Характеристикой интенсивности размерного износа является относительный (удельный) износ u0, т. е. износ в микрометрах, отнесенный к 1000м пути резания l:
.
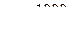Путь резания l определяется по формуле
,
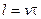где v - скорость резания в м/мин; t - время работы режущего инструмента.
Если известен относительный износ режущего инструмента, погрешность обработки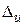 
, вызванная его размерным износом, может быть определена по следующим формулам:
а) для диаметральных размеров
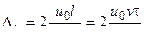мкм; (1)
б) для размеров длин
мкм. (2)
Этот вид погрешностей обычно определяется опытным путем для данных конкретных условий.
Вместе с износом режущего инструмента одновременно происходит и деформация его от нагрева в процессе резания.
Исследованиями установлено, что температурные деформации режущего инструмента Dl в зависимости от времени t его работы протекают по закону, показанному на рисунке 2.
До некоторого момента времени τс наблюдается интенсивное изменение размера режущего инструмента (например, удлинение резца), после чего температура режущего инструмента стабилизируется, и дальнейшее изменение его размера прекращается. По такому же закону происходит и изменение размеров обрабатываемой детали в связи с температурными деформациями режущего инструмента. Например, при обработке резцом наружных цилиндрических поверхностей диаметр каждой обрабатываемой детали сначала будет прогрессивно уменьшаться, а затем после некоторого периода времени τс размер стабилизируется, и функциональная погрешность после момента времени τс превратится в постоянную погрешность.
Если обработка производится с обильным охлаждением, то погрешности обработки, вызванные температурными деформациями режущего инструмента, имеют весьма малые значения и ими можно пренебречь.
При обработке деталей из штучных заготовок большое значение имеет время перерывов в работе режущего инструмента. Если время перерывов будет равно или больше времени работы инструмента, то за этот период инструмент полностью охладится, и изменение его размеров от нагрева для каждой новой детали будет носить постоянный характер и больше влиять на форму детали (например, конусность), чем на размер.
Погрешности от размерного износа режущего инструмента и от его температурных деформаций возникают одновременно и, суммируясь алгебраически, определяют характер изменения суммарной величины функциональных погрешностей обработки. В зависимости от длительности времени работы резца и времени перерывов, наличия или отсутствия доводки режущих граней инструмента суммарная величина функциональных погрешностей при одной настройке станка будет изменяться во времени по одному из следующих законов (рисунок 3).
 |
Кривая на рисунке 3, а характеризует изменение суммарной величины функциональных погрешностей обработки наружной поверхности Δf в зависимости от времени работы инструмента τ. При этом работа производится недоведенным режущим инструментом без охлаждения, время перерывов меньше времени работы инструмента и Δu > Δm.u в момент времени τн; здесь Δm.u - погрешность, вызванная температурными деформациями инструмента в этот же момент времени τн. Аналогичная картина будет иметь место, когда работа производится с охлаждением недоведенным инструментом.
Если же при тех же условиях погрешность Δu будет меньше погрешности Δm.u или если работа производится доведенным резцом без охлаждения и время перерывов инструмента меньше времени его работы, то будет иметь место кривая, показанная на рисунке 3, б.
При работе доведенным инструментом с охлаждением или без охлаждения, но при условии, что время перерывов равно или больше времени работы инструмента, график изменения функциональной погрешности обработки будет приближаться к прямой линии, наклоненной к оси абсцисс под некоторым углом (рисунок 3, в). При обработке внутренних поверхностей кривые изменения функциональных погрешностей во времени будут аналогичны, но повернуты относительно оси абсцисс на 180°.
Случайные погрешности обработки возникают от многих причин, но главными из них являются упругие деформации системы СПИЗ и зазоры в отдельных узлах станка.
Под влиянием колеблющейся силы резания, а также толчков и вибраций происходит неравномерное отжатие инструмента от обрабатываемой поверхности, а также неравномерный по величине и направлению выбор зазоров станка, что приводит к изменению размера обрабатываемой детали. Колебания силы резания возникают главным образом из-за неравномерного припуска на обработку и неравномерной твердости материала обрабатываемых деталей.
Наибольшее значение для образования случайных погрешностей обработки имеет составляющая силы резания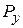 
, которая для точения определяется по следующей формуле:
.
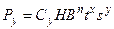Так как Су, НВп и tх не являются постоянными величинами и для каждой новой детали могут иметь свои значения, то предел колебания силы 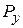для данной партии деталей будет равен
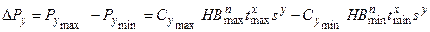(3)
Если известна жесткость j системы СПИД, то величина у отжатия режущего инструмента от обрабатываемой детали будет равна
.
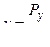Вместо жесткости j удобнее пользоваться обратной величиной, называемой податливостью W, которая равна
.
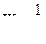Тогда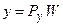 
.
Так как 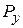колеблется в пределах 
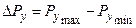, то и размеры обрабатываемых деталей в данной партии будут колебаться в пределах
.
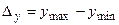Для обработки цилиндрических поверхностей это колебание размеров следует удвоить, т. е.
.
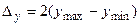Так как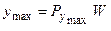 
и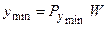 
, то при односторонней обработке деталей
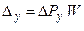(4)
и при обработке цилиндрических поверхностей
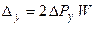. (5)
Если известны пределы колебаний НВ и t в данной партии заготовок, а также известно значение коэффициента Су для остро заточенного инструмента в начале обработки (и после его притупления в конце обработки) партии деталей, а также известна податливость системы, то предел колебания случайных погрешностей Ау может быть вычислен аналитически. Однако, учитывая приближенность эмпирической формулы для Ру, эти вычисления будут также носить приближенный характер.
Случайные погрешности, кроме перечисленных двух основных причин, возникают также в результате:
· неравномерности процесса резания;
· образования и срыва наростов на лезвии режущего инструмента;
· упругих деформаций детали под действием колеблющейся силы зажима;
· температурных деформаций обрабатываемой детали под влиянием колеблющейся температуры нагрева детали;
· несовпадения настроечных баз с конструкторскими;
· действия внутренних напряжений в материале заготовок;
· и других причин.
Все перечисленные причины обычно действуют одновременно и возникающие от них случайные погрешности суммируются, образуя результирующую величину случайных погрешностей для данной детали.
Таким образом, при обработке каждой новой детали возникают свои функциональные и свои случайные погрешности и, кроме того, у каждой детали имеется общая постоянная систематическая погрешность. Так как все эти погрешности возникают одновременно, то в сумме они образуют результирующую или суммарную погрешность обработки детали, которая и будет определять действительное отклонение размера от его номинального значения.
В силу изменчивости функциональных и случайных погрешностей суммарная погрешность обработки одной детали будет отличаться от суммарной погрешности другой детали. В результате этого возникает рассеивание погрешностей размеров и погрешностей формы деталей в партии, обработанной с одной настройки станка. Это рассеивание может подчиняться различным законам распределения. В частности, для погрешностей размеров часто находит применение закон нормального распределения.
Выбор закона нормального распределения для исследования погрешностей размера обосновывается теоремой Ляпунова, которую для рассматриваемого случая можно упрощенно представить следующим образом.
Если наблюдаемая величина х является суммой частных величин xi, вызванных действием значительного числа случайных и некоторого числа систематических факторов; если влияние всех случайных факторов на суммарную величину одного порядка, т. е. среди них нет резко доминирующих; если случайные факторы взаимно независимы и число их не изменяется во времени; если число систематических факторов остается одинаковым и постоянным во времени, то при выполнении этих условий и при достаточно большом числе слагаемых сумма последних будет следовать закону нормального распределения. Причем из теоремы Ляпунова следует, что каждое слагаемое может иметь какое угодно распределение. Сумма же их будет подчиняться закону нормального распределения, если число слагаемых достаточно велико и выполняются остальные условия теоремы Ляпунова.
Опыты показывают, что при работе на настроенных станках, если:
- среди возникающих случайных погрешностей обработки нет резко доминирующих;
- систематические погрешности не изменяются существенно во времени;
- работа протекает в нормальных условиях (станок, приспособление, инструмент находятся в исправном и хорошем состоянии),
то распределение действительных размеров партии деталей, обработанных на станке с одной настройки, подчиняется обычно закону нормального распределения.
Отступление от нормального закона распределения действительных размеров деталей в партии может быть вызвано в основном тремя причинами:
1) наличием доминирующей случайной погрешности или доминирующей систематической погрешности, закономерно изменяющейся во времени;
2) наличием переменного рассеивания из-за неполадок в станке или резкого колебания механических свойств материала обрабатываемых заготовок;
3)одновременным действием первой и второй причин.
При наличии первой причины суммарная погрешность размера деталей, например z, будет являться суммой доминирующей погрешности, например y, и других, мало отличающихся по своей величине, погрешностей xi, т. е.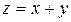 
, где x – сумма погрешностей xi. В этом случае закон распределения суммарной погрешности z действительных размеров деталей будет представлять собой композицию законов распределения погрешностей y и x.
В частности, если погрешность y подчиняется закону равной вероятности, в котором дифференциальная функция ее распределения определяется формулой
,
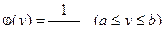а погрешность х подчиняется закону нормального распределения
,
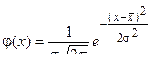то кривая распределения суммарной погрешности 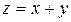обработки будет иметь вид, приведенный на рисунке 4.
Как следует из рисунка 4, графики плотности вероятности суммарной погрешности 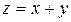содержат в себе элементы формы законов распределения суммируемых случайных величин. При этом форма кривой во многом определяется законом доминирующей случайной величиной. Так, в рассматриваемом случае форма кривой суммарной погрешности зависит от отношения
,
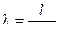где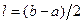 
; a, b, σx – параметры законов распределения величин y и x.
Поэтому с увеличением λ, т. е интервала значений погрешности y, кривая распределения суммарной погрешности 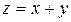обработки будет более плосковершинной, чем кривая нормального распределения (рисунок 4).
Вторая причина отступления распределения суммарной погрешности от закона нормального распределения (переменное рассеивание) приводит к более островершинным кривым по сравнению с нормальными кривыми. На практике условия возникновения распределений такого типа встречаются часто, так как к ним приводят, например, такие явления как затупление инструмента, вызывающее увеличение силы резания, следовательно, и увеличение упругих деформаций узлов станка; периодические колебания режима работы оборудования и др.
Распределения такого типа имеют место и в тех случаях, когда некоторые первичные факторы, увеличивающие рассеивание, действуют в течение только части времени изготовления партии деталей или периодически появляются и исчезают. Это имеет место, например, при резких колебаниях твердости материала, при обработке партии деталей на автомате из разных прутков.
Одновременное действие первой и второй причин отклонения фактического распределения погрешностей размера обработанных деталей от теоретического нормального обычно приводит к асимметричным или симметричным кривым распределения. При этом они могут быть остро- или плосковершинными кривыми в зависимости от того, какая из двух причин является доминирующей.
Таким образом, суммарная погрешность обработки партии деталей, обработанных с одной настройки станка, может иметь либо нормальное распределение, либо резко отличное от него. Однако при нормальных условиях течения процесса суммарная величина только случайных погрешностей, как правило, должна подчиняться закону нормального распределения, а при отсутствии доминирующих погрешностей и стабильности рассеивания случайных погрешностей и полная величина суммарной погрешности также должна подчиняться закону нормального распределения. Использование закона нормального распределения позволяет производить объективную оценку точности технологического процесса или отдельных его операций.
В общем виде суммарную погрешность обработки D для данной настроечной партии деталей можно выразить следующим уравнением:
, (6)
где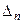 
- сумма постоянных погрешностей; 
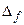- сумма функциональных погрешностей; 
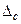- сумма случайных погрешностей; K и Kf- коэффициенты относительного рассеивания.
Суммарная погрешность обработки D представляет собой поле рассеивания действительных размеров деталей в данной партии. Поэтому сопоставление суммарной погрешности обработки D с допуском на размер 2d позволяет оценить точность обработки на данной операции.
Из уравнения (6) следует, что когда функциональные погрешности отсутствуют или имеют пренебрежимо малое значение, то поле рассеивания действительных размеров деталей определяется только случайными погрешностями, суммарная величина которых равна
,
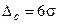где s - среднее квадратическое отклонение случайных погрешностей от их среднего значения.
Если функциональные погрешности являются доминирующими, то под их влиянием суммарная погрешность обработки будет изменяться во времени. В этом случае суммарная погрешность обработки должна определяться не вообще, а для вполне определенного времени с момента пуска станка. При этом должны определяться раздельно величины случайных и функциональных погрешностей. В связи с этим различают два вида распределений: мгновенное и суммарное распределение.
Под мгновенным распределением понимается такое распределение изучаемого признака в генеральной совокупности, которое имело бы место, если бы действие всех производственных факторов оставалось таким (или примерно таким), каким оно является в данный момент времени. Другими словами, функциональные погрешности оставались бы постоянными и равными по величине тому значению, какое они имеют в данный момент. Поэтому мгновенное распределение по существу является распределением только случайных погрешностей обработки.
Под суммарным распределением обычно понимается итоговое распределение изучаемого признака в партии деталей, изготовленных за период времени от наладки до подналадки станка.
Совокупность с мгновенным распределением будем называть мгновенной совокупностью. Малую текущую выборку из продукции, обрабатываемой на настроенном станке, можно рассматривать как выборку из мгновенной совокупности, подчиняющейся определенному закону распределения. Если речь идет о погрешностях размеров деталей, то можно считать, что мгновенная совокупность подчиняется закону нормального распределения.
При обработке мелких деталей на автоматах, когда машинное время обработки отдельных поверхностей измеряется в десятых или сотых долях минуты, большую выборку из текущей продукции станка также можно рассматривать как выборку из мгновенной совокупности, так как функциональные погрешности в этом случае будут ничтожно малы. По такой выборке можно установить и закон распределения мгновенной совокупности или закон распределения только случайных погрешностей.
Дата: 2019-02-25, просмотров: 383.
