Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

IV типа точности

 

Для процесса IV типа точности (рисунок 1)суммарная погрешность обработки составляет

,

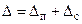где 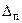 - постоянные погрешности;  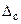- случайные погрешности.

Для определения суммарной величины случайных погрешностей во всей настроечной партии необходимо в качестве оценки σ₀ принять 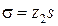, где s - среднее квадратическое отклонение выборки, а z₂ - коэффициент, определяемый в зависимости от объема выборки по таблице П5 приложения. Тогда

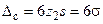.             (1)

 

Фактическая величина постоянных погрешностей 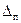 или резерв допуска, приходящийся на долю постоянных погрешностей, определяется по следующим формулам:

а) для наружных поверхностей

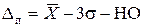;                                          (2)

б) для внутренних поверхностей

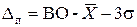,                                           (3)

где ВО и НО — верхнее и нижнее предельные отклонения измеряемого размера с учетом их знаков; 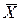 - среднее арифметическое значение отклонений действительных размеров x_i от номинального размера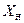

.

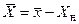Для оценки точности процесса необходимо сравнить полученную суммарную погрешность Δ с допуском 2δ на размер детали. Точность процесса считается достаточной или избыточной, если удовлетворяется неравенство

Δ ≤ 2δ.

Однако на практике возможен брак даже и при избыточной точности процесса, если настройка станка была выполнена с погрешностью, величина которой превышала допустимое значение.

Обозначим через Δ₀ координату середины поля допуска относительно номинального значения размера 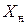. Координата Δ₀ определяется по формуле

,

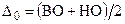где ВО и НО — верхнее и нижнее предельные отклонения размера по чертежу с учетом знаков.

Тогда величина смещения среднего значения 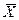 от Δ₀ составит:

.

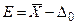На рисунке 2, а показаны два крайних положения кривой нормального распределения отклонений измеряемого размера в поле его допуска Δ₀, когда смещение E среднего 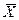 от координаты середины поля допуска Δ₀ находится в пределах допустимых значений. На рисунке 2, б приведены два других крайних положения кривой нормального распределения отклонений измеряемого размера, когда  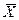смещено относительно Δ₀ на величину, превышающую допустимое значение. При таком смещении E среднего  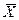от координаты середины поля допуска Δ₀ возникает брак, т. е. часть деталей q₁ или q₂ будет иметь отклонения размеров, выходящие за пределы допуска.

Рисунок 2. Допустимые (а) и недопустимые (б) смещения центра рассеивания

Погрешностей

 

Из рисунка 2, а видно, что допускаемая погрешность настройки Δ_н.д. режущего инструмента на размер равна

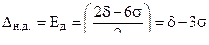.                                    (4)

Фактическая величина погрешности настройки Δ_н.д. определяется по формуле

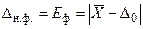.                                                    (5)

Для работы без брака должно быть соблюдено неравенство

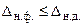.                                                (6)

Если это неравенство не будет соблюдено и 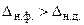, то при обработке настроечной партии неизбежен брак даже при избыточной точности процесса. Вероятный процент этого брака (рис. 2, б) можно определить по формуле

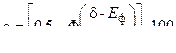.                                  (7)

Для сравнительной оценки точности аналогичных операций можно пользоваться коэффициентом точности K_т:

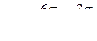.                                          (8)

При K_т ≤ 1 точность процесса достаточная, а при K_т > 1 недостаточная. Для оценки точности настройки станка пользуются коэффициентом точности настройки e:

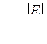.                                                 (9)

При этом допустимое значение e_д:

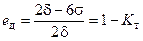.                                      (10)

Фактическое значение е_ф определится по формуле

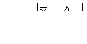.                                           (11)

Условия работы без брака выразятся неравенствами:

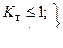                                              (12)

Для оценки устойчивости процесса по большой выборке достаточно подтверждений гипотез нормальности и случайности выборки. Если эти гипотезы подтверждаются, то процесс можно считать устойчивым во времени.

Пример выполнения статистического анализа устойчивости и точности процессов IV типа точности

Задача. С одношпиндельного токарно-револьверного автомата, обрабатывающего ролики 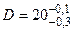 мм, взята выборка n = 50. Ролики были измерены по диаметру микрометром с ценой деления 0,01 мм. Результаты измерений деталей выборки приведены в таблице 2.

Необходимо определить точность процесса, его устойчивость, точность настройки и возможный процент брака при данной настройке станка на размер.

Статистический анализ данных выборки. При выполнении отдельных этапов статистического анализа будем использовать возможности процессора Excel.

Таблица 2. Результаты измерений диаметра роликов в мм

 

Номер ролика	D	Номер ролика	D	Номер ролика	D	Номер ролика	D	Номер ролика	D
1	19,81	11	19,82	21	19,82	31	19,85	41	19,83
2	19,83	12	19,84	22	19,85	32	19,84	42	19,84
3	19,84	13	19,84	23	19,84	33	19,85	43	19,85
4	19,85	14	19,87	24	19,80	34	19,86	44	19,87
5	19,86	15	19,88	25	19,88	35	19,87	45	19,89
6	19,83	16	19,83	26	19,85	36	19,82	46	19,85
7	19,84	17	19,84	27	19,84	37	19,83	47	19,84
8	19,85	18	19,85	28	19,85	38	19,84	48	19,85
9	19,86	19	19,86	29	19,86	39	19,85	49	19,86
10	19,86	20	19,86	30	19,87	40	19,86	50	19,87

 

1. Вычисление статистических характеристик выборки 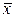и s . Заполним массив ячеек A2:E11 и ячейку F2 рабочего листа Excel результатами измерений деталей выборки (таблица 3). В ячейки F4 и F6 введем формулы вычисления характеристик 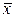и s, используя статистические функции Excel СРЗНАЧ, КОРЕНЬ и ДИСП.

Получим ; .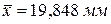

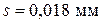Таблица 3. Результаты вычисления характеристик 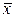и s

 

	A	B	C	D	E	F
1	Исходные данные xi					n
2	19,81	19,82	19,82	19,85	19,83	50
3	19,83	19,84	19,85	19,84	19,84
4	19,84	19,84	19,84	19,85	19,85	19,848
5	19,85	19,87	19,80	19,86	19,87	s
6	19,86	19,88	19,88	19,87	19,89	0,01807
7	19,83	19,83	19,85	19,82	19,85
8	19,84	19,84	19,84	19,83	19,84
9	19,85	19,85	19,85	19,84	19,85
10	19,86	19,86	19,86	19,85	19,86
11	19,86	19,86	19,87	19,86	19,87

 

2. Проверка гипотез о случайности выборки. Эта проверка позволяет установить наличие или отсутствие функциональных погрешностей обработки, обуславливающих смещение центра рассеивания (статистики ).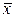

При наблюдениях за размерами обрабатываемых деталей на настроенном станке, проверку гипотезы случайности выборки осуществляют методом последовательных разностей.

Проверка гипотезы случайности выборки методом последовательных разностей заключается в вычислении критерия t

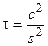                                                    (13)

и сравнения полученного значения с критическим t_q его значением.

Если 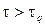, то гипотеза случайности выборки принимается, в противном случае отвергается.

В формуле (13) величина c² представляет несмещенную оценку σ² по данным выборки и определяется по выражению

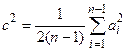,                                     (14)

в котором a_i - разность между соседними членами х _i+1 и х _i данных выборки, a_i = х _i+1 – х _i (i = 1, 2,…, n - 1).

Критическое значение t_q при n > 20 вычисляется по формуле

,

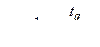где величина t_q определяется из соотношения , в котором 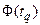 является функцией Лапласа  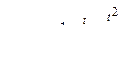(таблица П1 приложения);

q - принятый уровень значимости (обычно q = 5%).

Для определения значения критерия t вычислим, прежде всего, величину c². Для этого из каждого последующего значения размера детали, приведенного в таблице 2, начиная со второго, вычтем предыдущее значение размера и, таким образом, составим 49 разностей, каждую из которых возведем в квадрат. Например,

₁=19,83-19,81=0,02 мм; a₂=19,84- 19,83=0,01мм и т. д.

В таблице 4 приведены результаты выполнения перечисленных операций в среде Excel (массив A14:E23). В ней же в ячейках G15 и G17 приведены результаты вычисления величины c² и критерия t по формулам (14) и (13).

 

Таблица 4. Результаты вычисления критерия t

 

	A	B	C	D	E	F	G
13	Вычисление квадратов разностей аi2=(xi+1-xi), i=1,2,…, n
14	0,0004	0,0004	0,0009	0,0001	0,0001		c2
15	0,0001	0,0000	0,0001	0,0001	0,0001		0,000278
16	0,0001	0,0009	0,0016	0,0001	0,0004		τ = c2/s2
17	0,0001	0,0001	0,0064	0,0001	0,0004		0,85
18	0,0009	0,0025	0,0009	0,0025	0,0016
19	0,0001	0,0001	0,0001	0,0001	0,0001
20	0,0001	0,0001	0,0001	0,0001	0,0001
21	0,0001	0,0001	0,0001	0,0001	0,0001
22	0,0000	0,0000	0,0001	0,0001	0,0001
23	0,0016	0,0016	0,0004	0,0009

 

Для вычисления критического значения t_q зададим уровень значимости q = 5%. По формуле   находим 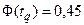, которому по таблице П1 приложения значений функции Лапласа соответствует t_q =1,65, следовательно,

.

Так как 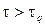 (0,85>0,77), то гипотеза «случайности» выборки верна с вероятностью α = 1-0,05 = 0,95.

 

3. Проверка гипотезы о нормальном распределении. Проверку гипотезы нормальности распределения генеральной совокупности по взятой из нее выборке выполним по критерию l (см. тему 4).

Для определения значения критерия λ вычислим значения эмпирической 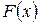 и теоретической  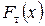функций нормального закона распределения и их разности  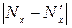для каждого наблюденного значения случайной величины х по формулам

; ,

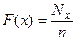в которых 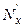 и 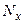 - накопленные теоретические и эмпирические частоты.

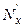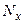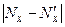Выполняя все вычисления в среде Excel, получим результаты вычисления ,  и , приведенные в таблице 5. Максимальная разность этих функций составляет 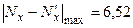.Следовательно, величина критерия l составит

.

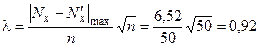Таблица 5. Результаты вычисления теоретических частот ,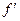

накопленных частот 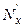,  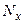и их разности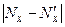

Интервалы	Середина интервала xi	f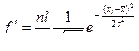
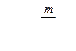
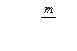
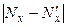
19,81—19,82	19,815	1	2,064	1	2,08	1,08
19,82—19,83	19,825	3	4,899	4	6,98	2,98
19,83—19,84	19,835	5	8,538	9	15,52	6,52
19,84—19,85	19,845	11	10,929	20	26,45	6,45
19,85—19,86	19,855	12	10,275	32	36,72	4,72
19,86—19,87	19,865	10	7,094	42	43,82	1,82
19,87—19,88	19,875	5	3,598	47	47,42	0,42
19,88—19,89	19,885	2	1,340	49	48,76	0,24
19,89—19,90	19,895	1	0,367	50	49,12	0,88
		50	49,103

 

По таблице П6 приложения этому значению l соответствует 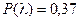. Эта вероятность больше 0,05. Поэтому нашу нулевую гипотезу считаем верной.

Поскольку гипотезы нормальности и случайности выборки являются верными, то процесс обработки роликов можно считать устойчивым во времени, и он может быть отнесен к IV типу точности.

4. Определение погрешности обработки. Суммарная погрешность обработки для процесса IV типа точности равна

.

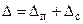Для вычисления Δ_с определим оценку σ для среднего квадратического отклонения σ₀ генеральной совокупности:

 

σ = z₂s = 1,246·0,018 = 0,0224мм,

 

где значение z₂ взято из таблицы П5 приложения. Следовательно, случайная погрешность составит

Δ_с = 6σ = 6·0,0224 =0,1344мм.

 

Постоянные погрешности равны

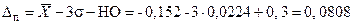мм,

где координата 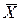 среднего арифметического значения  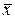составляет

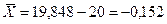мм.

Так как 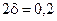мм, а 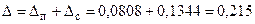мм, т.е. 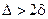, то процесс не обеспечивает требуемую точность.

 

5. Выявление причин погрешности обработки. На рисунке 3 показано графическое представление фактического рассеивания размеров деталей в поле допуска. На рисунке приведены:

· -координата середины поля допуска, которая равна

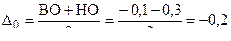мм;

· -координата 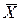 среднего арифметического значения ;

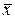· -фактическое смещение центра рассеивания относительно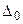

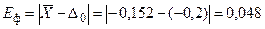мм;

Вместе с тем, допускаемое смещение центра рассеивания (допуск на настройку) равно

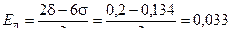мм.

Рисунок. 3. Кривая распределения размеров роликов

 

Так как 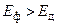, то возможен брак в партии деталей, процент которых может составить

 

 

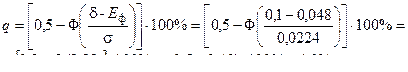
Как следует из рисунка 3, основной причиной погрешности обработки в рассматриваемом примере служит неправильная настройка станка. За счет изменения настройки станка можно снизить постоянную погрешность Δ_п.

Во избежание появления брака необходимо изменить настройку так, чтобы 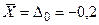мм или, приняв допуск на настройку 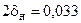мм, т. е. положив 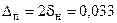мм, необходимо стремиться получить при настройке координату  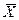среднего арифметического значения  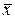равную

 

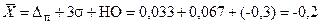мм

или необходимо, чтобы

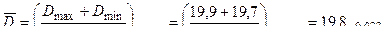мм.

Если в результате статистического анализа установлено, что сумма случайных погрешностей Δ_с равна допуску 2δ на размер или близка к нему, то необходимо выяснить доминирующую причину возникновения случайных погрешностей.

При токарной обработке случайные погрешности можно разделить на два вида: на погрешности Δ_y, зависящие от жесткости системы СПИЗ, и на погрешности Δ_з, которые возникают главным образом от наличия зазоров в отдельных частях станка. Под влиянием колеблющейся силы резания и вибраций эти зазоры выбираются в процессе обработки неравномерно как по величине, так и направлению, вызывая колебания размеров у обрабатываемых деталей.

Суммарную величину случайных погрешностей Δ_с можно, таким образом, представить в виде двух слагаемых:

 

.

Величину 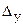, можно определить по формуле

,

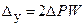где 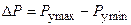; W - податливость системы, определяемая производственным методом; K_у и K_з - коэффициенты относительного рассеивания, которые можно принять равными K_у = K_з = 1,2. Зная величину 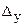, можно определить  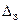по формуле

.

Величина 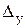 будет характеризовать жесткость станка, величина  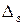- его точность. Если  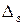> 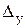, то причиной недостаточной точности обработки является плохое состояние станка, если  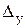> 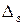, то причиной является малая жесткость станка.