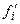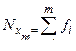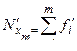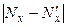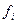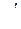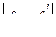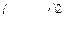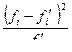Величины
Проверка гипотезы о законе распределения случайной величины включает в себя выполнение следующих процедур:
6. Вычисление теоретических значений частот 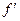 , используя дифференциальную функцию предполагаемого закона распределения, параметры которого принимают равными статистическим параметрам выборки.
, используя дифференциальную функцию предполагаемого закона распределения, параметры которого принимают равными статистическим параметрам выборки.
7. Построение по значениям статистических и теоретических частот графиков соответствующих распределений. Визуальная оценка близости эмпирического распределения к предполагаемому теоретическому закону.
8. Вычисление критерия согласия, оценивающего степень согласованности теоретического и статистического распределений.
9. Сопоставление расчетного значения критерия согласия с его табличным, называемым критическим значением. Принятие решения о достоверности гипотезы о законе распределения исследуемой случайной величины или отбрасывании ее, как противоречивой опытным данным.
Для проверки гипотезы о нормальном распределении генеральной совокупности по большой выборке из нее можно использовать как критерий l, так и критерий χ2.
Пример 2. Используя результаты выравнивания статистической совокупности примера 1, выполнить проверку гипотезы о нормальном распределении генеральной совокупности, из которой произведена большая выборка погрешности обработки роликов.
Для вычисления λ по формуле (5) составим таблицу 9 на основании данных таблицы 4. Вычисление 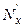 и
и 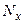 производится путем прибавления к каждому значению
производится путем прибавления к каждому значению 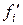 или
или 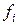 суммы предшествующих значений
суммы предшествующих значений 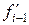 или
или 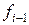 .
.
Таблица 9. Данные для вычисления критерия l
| xi | fi |
|
|
|
|
| -0,17 | 0 | 0,06 | 0,00 | 0,06 | 0,06 |
| -0,15 | 0 | 0,59 | 0,00 | 0,65 | 0,65 |
| -0,13 | 3 | 3,33 | 3,00 | 3,99 | 0,99 |
| -0,11 | 16 | 11,35 | 19,00 | 15,33 | 3,67 |
| -0,09 | 22 | 23,18 | 41,00 | 38,51 | 2,49 |
| -0,07 | 25 | 28,42 | 66,00 | 66,93 | 0,93 |
| -0,05 | 19 | 20,93 | 85,00 | 87,86 | 2,86 |
| -0,03 | 13 | 9,25 | 98,00 | 97,11 | 0,89 |
| -0,01 | 2 | 2,46 | 100,00 | 99,57 | 0,43 |
| Σ | 100 | 99,57 |
|
|
|
По формуле (5) имеем 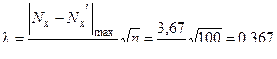 .
.
По таблице П6 приложения этому значению l соответствует 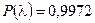 . Эта вероятность близка к единице. Поэтому можно нашу нулевую гипотезу считать верной.
. Эта вероятность близка к единице. Поэтому можно нашу нулевую гипотезу считать верной.
Выполним проверку гипотезы о нормальном распределении по критерию χ2. Вычисление критерия χ2 произведем с помощью таблицы 10, составленной по данным таблицы 4. Так как частоты 1 и 7-го интервалов менее 5, то они объединены с соседними интервалами. Результаты вычисления теоретических и эмпирических частот 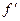 и
и 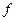 и критерия χ2 приведены в таблицы 10.
и критерия χ2 приведены в таблицы 10.
По таблице 10 имеем  . Число степеней k = т – р- 1 = 5 – 2 - 1 = 2, где m = 5 – число интервалов, р = 2 – число параметров закона распределения. По таблице П7 приложения
. Число степеней k = т – р- 1 = 5 – 2 - 1 = 2, где m = 5 – число интервалов, р = 2 – число параметров закона распределения. По таблице П7 приложения 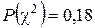 . Эта вероятность больше доверительной вероятности
. Эта вероятность больше доверительной вероятности 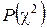 = 0,05, следовательно, и по критерию
= 0,05, следовательно, и по критерию 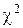 нашу нулевую гипотезу можно считать верной.
нашу нулевую гипотезу можно считать верной.
Таблица 10. Результаты вычисления 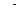
| x |
|
|
|
|
| |||
| от | до | |||||||
| -0,14 | -0,12 | 3 |
19 | 3 |
14 | 5 | 25 | 1,78 |
| -0,12 | -0,10 | 16 | 11 | |||||
| -0,10 | -0,08 | 22 | 23 | 1 | 1 | 0,043 | ||
| -0,08 | -0,06 | 25 | 29 | 4 | 16 | 0,550 | ||
| -0,06 | -0,04 | 19 | 22 | 3 | 9 | 0,410 | ||
| -0,04 | -0,02 |  13 13
| 15 |  9 9
| 12 | 3 | 9 | 0,750 |
| -0,02 | -0,00 | 2 | 3 | |||||
|
| 
| |||||||
Процедура вычисления критерия l и 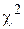 для проверки гипотезы близости эмпирического распределения любому другому теоретическому закону распределения остается аналогичной рассмотренной в данном примере. Отличие будет заключаться лишь в вычислении теоретических частот или теоретических функций распределения F(х).
для проверки гипотезы близости эмпирического распределения любому другому теоретическому закону распределения остается аналогичной рассмотренной в данном примере. Отличие будет заключаться лишь в вычислении теоретических частот или теоретических функций распределения F(х).
Контрольные вопросы
1. Дайте определение понятию «статистическая гипотеза». В чем отличие параметрических гипотез от непараметрических гипотез? Как называют критерии проверки достоверности параметрических и непараметрических гипотез?
2. Какие гипотезы наиболее часто проверяют в статистических исследованиях процессов механической обработки деталей?
3. Сформулируйте нуль-гипотезу о законе распределения случайной величины.
4. В чем различие критериев значимости и критериев согласия по их назначению?
5. Что собой представляют простая статистическая совокупность и статистический ряд?
6. Что учитывают при определении закона статистического распределения случайной величины?
Лекция 5
Дата: 2019-02-25, просмотров: 384.