Пусть имеются две серии независимых испытаний однородных величин х и у. При этом наблюденные значения х i,и у i дают различные значения средних ( 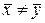 ) или обнаруживают различные рассеивания (
) или обнаруживают различные рассеивания ( 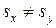 ). Возникает вопрос, можно ли считать эти расхождения существенными или они носят случайный характер. Например, с двух станков, настроенных на обработку одних и тех же деталей, взяты две текущие выборки. Средние и дисперсии этих выборок отличаются друг от друга. При этом закон распределения генеральных совокупностей, из которых взяты выборки, неизвестен. Требуется проверить, обеспечивают ли оба станка одинаковую точность обработки.
). Возникает вопрос, можно ли считать эти расхождения существенными или они носят случайный характер. Например, с двух станков, настроенных на обработку одних и тех же деталей, взяты две текущие выборки. Средние и дисперсии этих выборок отличаются друг от друга. При этом закон распределения генеральных совокупностей, из которых взяты выборки, неизвестен. Требуется проверить, обеспечивают ли оба станка одинаковую точность обработки.
Нулевая гипотеза в данном случае будет заключаться в том, что функции распределения х и у тождественны, т. е. выборки принадлежат одной и той же генеральной совокупности. Для проверки этой нулевой гипотезы может быть использован критерий Вилькоксона, основанный на числе инверсий. Под инверсиями в данном случае понимается следующее. Наблюденные значения х и у в двух выборках располагают в общую последовательность в порядке возрастания, например, в виде
y1 y2 x1 x2 y3 y4 y5 x3 y6 x4 ,
где x1,…, x4 - члены первой выборки, а y1,…, y6 - члены второй выборки.
Если какому-либо значению х предшествует некоторый у, то говорят, что эта пара дает инверсию. Если некоторому значению х m предшествует n значений у, то это значит, что х m имеет n инверсий. Например, в нашей последовательности х1 дает две инверсии, х2 - то же две инверсии, х3 — пять инверсий и х4 — шесть инверсий. Всего инверсий в нашей последовательности будет
u = 2 + 2 + 5 + 6= 15.
Нулевая гипотеза принимается, если число u будет лежать внутри некоторых предельных (критических) значений, вычисляемых для принятого уровня доверительной вероятности. Расчет критических значений для u производится из следующих соображений. Если объемы выборок n > 10 и m >10, то число инверсий u распределяется приблизительно по нормальному закону со средним значением (математическим ожиданием)
 (17)
(17)
и дисперсией
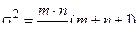 . (18)
. (18)
Поэтому предельные значения и определяются границами
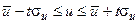 , (19)
, (19)
где t зависит от принятого уровня доверительной вероятности и вычисляется по таблице значений Ф(t) (табл. П1 приложения) по формуле
q = 1 - 2Ф(t) ,
откуда
 (20)
(20)
Например, для q = 0,05 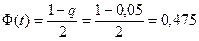 . Этому значению Ф(t) по таблице П1 соответствует t = 1,96.
. Этому значению Ф(t) по таблице П1 соответствует t = 1,96.
Таким образом, если наблюденное значение u будет лежать внутри границ, определяемых неравенством (19), или не выходить за пределы критических областей
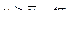 , (21)
, (21)
то нулевая гипотеза принимается, в противном случае она отвергается. Так как u имеет приближенно нормальное распределение только при выборках объема u > 10 и m > 10, то для использования критерия Вилькоксона необходимо брать выборки объемом не менее 12.
Пример 7. С двух станков, настроенных на обработку одной и той же детали, взяты текущие выборки объема n = m = 15. Результаты измерения деталей выборок приведены в табл. 4, где через х обозначены отклонения измеряемого размера от номинала в мкм для выборки со станка № 1, а через у - отклонения в мкм измеряемого размера для выборки со станка № 2.
Требуется определить, можно ли считать точность обработки двух станков одинаковой. Другими словами, нужно проверить нулевую гипотезу о том, что распределения погрешностей обработки двух станков описываются одинаковыми функциями распределения.
Таблица 4. Результаты измерения деталей выборок, мкм
| Станок | Обозначение | Порядковый номер обработанных деталей | ||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 
| s | ||
| № 1 | x | 14 | 20 | 27 | 13 | 23 | 17 | 14 | 9 | 10 | 19 | 17 | 13 | 11 | 4 | 5 | 14,4 | 6,3 |
| № 2 | y | 4 | 18 | 3 | 10 | 8 | 20 | 10 | 11 | 16 | 10 | 13 | 20 | 15 | 21 | 8 | 12,5 | 6 |
Расположим данные таблице 4 в общую последовательность в порядке возрастания результатов измерения (таблице 5).
Таблица 5. Значения х и у в последовательности возрастания их величин
| у | у | x | x | у | у | x | у | у | у | x | у | x | у | x |
| 3 | 4 | 4 | 5 | 8 | 8 | 9 | 10 | 10 | 10 | 10 | 11 | 11 | 13 | 13 |
| x | x | x | у | у | x | x | у | x | у | у | x | у | x | x |
| 13 | 14 | 14 | 15 | 16 | 17 | 17 | 18 | 19 | 20 | 20 | 20 | 21 | 23 | 27 |
Число инверсий для х будет равно
u = 2 + 2 + 4 + 7 + 8 + 9 + 9 + 9 + 9+11+11 + 12+14 + 15+15= 137.
По формулам (17) и (18) находим
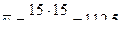 ;
; 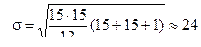 .
.
Задаваясь уровнем значимости q = 0,05 и принимая во внимание, что при q = 0,05 t = 1,96, определим критические значения для u:
u ≥ 112,5 - 1,96 ∙ 24 ≈ 66; u ≤ 112,5 + 1,96 ∙ 24 ≈ 158.
Полученное значение инверсии u = 137 не выходит за пределы критической области. Поэтому наша нулевая гипотеза не опровергается и, следовательно, нет основания считать, что станки существенно отличаются по точности.
Контрольные вопросы
1. Поясните требования к оценкам параметров генеральной совокупности, например, оценок 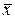 и s соответствующих параметров
и s соответствующих параметров 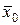 и σ0 генеральной совокупности: «они должны быть состоятельными и несмещенными».
и σ0 генеральной совокупности: «они должны быть состоятельными и несмещенными».
2. Какой критерий применяют при проверке гипотезы случайности выборки способом последовательных разностей? Как определяется его расчетное значение?
3. Как определяется критическое значение критерия t?
4. Выполнение каких двух условий позволяет принять гипотезу случайности выборки при проверке ее способом числа и длины серий?
5. При выполнении какого условия может быть принята гипотеза равенства двух выборочных средних? Поясните его.
6. Сформулируйте гипотезу равенства двух выборочных дисперсий. При выполнении какого условия эта гипотеза может быть принята, если выборки взяты из нормальной генеральной совокупности? Поясните его.
Лекция 6
Дата: 2019-02-25, просмотров: 385.