Для описания и изучения свойств генеральной совокупности по выборке из нее необходимо, чтобы выборка была репрезентативной (представительной). Репрезентативной может быть только случайная выборка. Напомним, что выборка считается случайной, если все объекты генеральной совокупности имеют равную возможность попасть в выборку.
Для проверки гипотезы случайности выборки может быть использовано два способа: способ последовательных разностей и способ числа и длины серий. Если можно допустить, что в течение наблюдений центр распределения величины х постепенно меняется, но дисперсия остается постоянной, то для проверки гипотезы «случайности» выборки является удобным и вполне приемлемым способ последовательных разностей. Такой случай часто имеет место при наблюдениях за размерами обрабатываемых деталей на настроенном станке, когда, вследствие износа инструмента, нагревания станка, циклических погрешностей многопозиционных станков и т. п., центр рассеивания постепенно смещается и, таким образом, происходит медленное и достаточно плавное изменение средней 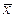 при неизменном стандарте σ, характеризующем рассеивание размеров.
при неизменном стандарте σ, характеризующем рассеивание размеров.
Способ последовательных разностей заключается в следующем: по наблюденным значениям х i выборки, расположенным в последовательности их наблюдения: х1, х2, х3, . . ., х n, образуют n - 1 разностей между соседними членами:
a1 = х2 – х1;
a2 = х3 – х2;
…………..;
an -1 = х n – х n-1;
Доказано, что если выборка взята из генеральной совокупности с параметрами 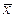 и σ2, то математическое ожидание Ма2 величины a2 будет равно:
и σ2, то математическое ожидание Ма2 величины a2 будет равно:
Ма2 = 2s2. (1)
Так как состоятельной и несмещенной оценкой математического ожидания является средняя арифметическая, то взяв среднюю арифметическую из величин 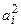 и разделив ее на два, мы получим несмещенную оценку σ2 по данным выборки, которую обозначим c2:
и разделив ее на два, мы получим несмещенную оценку σ2 по данным выборки, которую обозначим c2:
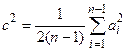 . (2)
. (2)
С другой стороны, для обычной несмещенной оценки σ2 имеем
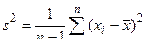 .
.
Таким образом, мы имеем две несмещенные оценки σ2: c2 и s2. Когда центр распределения ( 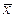 ) изменяется достаточно медленно и плавно при неизменном σ2, это мало скажется на последовательных разностях, а следовательно, и на величине c2. Однако это изменение значительно отразится на величине s2, так как в формулу вычисления последней входит непосредственно величина
) изменяется достаточно медленно и плавно при неизменном σ2, это мало скажется на последовательных разностях, а следовательно, и на величине c2. Однако это изменение значительно отразится на величине s2, так как в формулу вычисления последней входит непосредственно величина 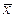 .
.
В связи с указанным для оценки «случайности» выборки при наличии возможности смещения центра рассеивания (при неизменном σ) целесообразно использовать критерий t:
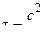 (3)
(3)
При этом малые значения t следует считать указывающими на неверность гипотезы «случайности» выборки.
При n > 20 критерий t будет иметь нормальное распределение, если выборки будут действительно случайны. Поэтому критическая область для t, отвечающая q % уровню значимости при n > 20, будет определяться неравенством 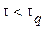 , в котором
, в котором
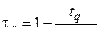 .
.
Значение tq определяется из соотношения 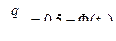 .
.
Откуда
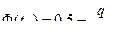 .
.
Заметим, что функция 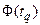 является функцией Лапласа
является функцией Лапласа 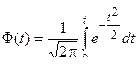 . Зная
. Зная 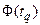 по таблице П1 приложения можно определить
по таблице П1 приложения можно определить  . Например, n = 24 при q = 5%,
. Например, n = 24 при q = 5%, 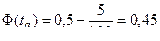 . По таблице П1 приложения этому значению функции соответствует tq =1,65, следовательно,
. По таблице П1 приложения этому значению функции соответствует tq =1,65, следовательно, 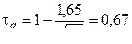 . Если вычисленное по данным 24-х наблюдений τ будет меньше 0,67, то это укажет на неверность нашей гипотезы о «случайности». Если же τ окажется больше 0,67, то гипотеза «случайности» будет верна с вероятностью
. Если вычисленное по данным 24-х наблюдений τ будет меньше 0,67, то это укажет на неверность нашей гипотезы о «случайности». Если же τ окажется больше 0,67, то гипотеза «случайности» будет верна с вероятностью 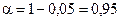 .
.
Пример 1. n = 20, s2 = 0,133 мм2, с2 = 0,127.
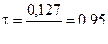 .
.
По таблице 1 при n = 20 нижняя граница для критерия t при 5%-ном уровне значимости равна  , т. е.
, т. е. 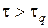 . Следовательно, гипотеза «случайности» верна.
. Следовательно, гипотеза «случайности» верна.
Таблица 1. Нижние пределы значений критерия tq
| Число наблюдений n | Уровни значимости q | Число на-блюдений n | Уровни значимости q | Число на-блюдений n | Уровни значимости q | ||||
| 1% | 5% | 1% | 5% | 1% | 5% | ||||
| 4 | 0,256 | 0,390 | 10 | 0,376 | 0,531 | 16 | 0,475 | 0,614 | |
| 5 | 0,269 | 0,410 | 11 | 0,397 | 0,548 | 17 | 0,487 | 0,624 | |
| 6 | 0,281 | 0,445 | 12 | 0,414 | 0,564 | 18 | 0,499 | 0,633 | |
| 7 | 0,307 | 0,468 | 13 | 0,431 | 0,578 | 19 | 0,510 | 0,642 | |
| 8 | 0,331 | 0,491 | 14 | 0,447 | 0,591 | 20 | 0,520 | 0,650 | |
| 9 | 0,354 | 0,514 | 15 | 0,461 | 0,603 | ||||
Способ длины и числа серий. Пусть имеется последовательность, в которой наблюдается случайное чередование m элементов, состоящее из n1 элементов первого рода и n2 элементов второго рода. Если обозначить элементы первого рода буквой a, а элементы второго рода буквой b, то такую последовательность можно представить в виде чередования букв a и b, например:
a a a b b a a b a a b b b b a a b b a b.
Данная последовательность состоит из 10 элементов a и 10 элементов b, т. е. n1 = 10, n2 = 10 и m = n1 + n2 = 10 + 10 = 20.
Совокупность следующих друг за другом одинаковых элементов называется серией. Число элементов, входящих в серию, называется длиной серии. В нашем примере последовательность состоит из 10 серий, в том числе имеется 5 серий из элементов a и 5 серий из элементов b. Эти серии расположены в следующей последовательности: серия a состоит из трех элементов, серия b – из двух, серия a – из двух, серия b – из одного элемента и т. д. Следовательно, длины этих серий равны: 3, 2, 2, 1 и т. д. Обозначим буквой K наибольшую длину серии любого элемента, а буквой R — общее число серий элементов a и b. В нашем примере K = 4, R = 10.
Для величин K и R в случайных выборках из совокупностей с непрерывным распределением найдены законы их распределения. С помощью этих законов вычислены критические значения K и R в случайных выборках объема n = 10 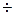 200 при доверительном уровне вероятности q = 0,05 (таблицы 2, 3). Эти критические значения K и R используются в качестве критериев для проверки гипотезы «случайности» выборки.
200 при доверительном уровне вероятности q = 0,05 (таблицы 2, 3). Эти критические значения K и R используются в качестве критериев для проверки гипотезы «случайности» выборки.
Таблица 2. Критические значения наибольшей длины серии K в случайных выборках объема n при доверительной вероятности q = 0,05
| n | 10 | 14 | 22 | 34 | 54 | 86 | 140 | 230 |
| K | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Таблица 3. Критические значения чисел серий R в случайной выборке объема n
при доверительной вероятности q = 0,05:
| n | 10 | 20 | 30 | 40 | 50 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| R | 3 | 6 | 11 | 15 | 19 | 24 | 33 | 42 | 51 | 60 | 70 | 79 | 88 |
Из приведенных в таблице 1 данных следует, что, например, в выборке объема n = 10, если она случайна, появление серии длиной K = 5 или более имеет вероятность q = 0,05. Такую же вероятность имеет появление серии длиной K ≥ 6 для выборок объема n = 11 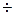 14.
14.
Так как вероятность q = 0,05 очень мала, а маловероятные явления практически осуществляются очень редко или почти не осуществляются, то появление в выборке объема n = 10 серии длиной K = 5 или более укажет на то, что данная выборка является не случайной.
Из приведенных в таблице 2 данных следует, что, например, в выборке объема n = 10, если она случайна, можно встретить общее число серий R ≤ 3 только с вероятностью q = 0,05, а в выборке объема n= 41 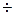 50 с такой же вероятностью можно встретить R ≤ 19. Поэтому, если в действительности в выборках объема n встретится такое общее число серий R, какое указано выше для соответствующего n или менее этого числа R, то в силу принципа практической невозможности маловероятных явлений надо считать наблюденное число серий, а следовательно, и выборку не случайными.
50 с такой же вероятностью можно встретить R ≤ 19. Поэтому, если в действительности в выборках объема n встретится такое общее число серий R, какое указано выше для соответствующего n или менее этого числа R, то в силу принципа практической невозможности маловероятных явлений надо считать наблюденное число серий, а следовательно, и выборку не случайными.
Таким образом, если обозначим наблюденное значение длины серии в выборке буквой Kн, а наблюденное значение общего числа серий Rн, то для принятия гипотезы случайности выборки необходимо выполнение следующих двух условий одновременно:
Kн < K, Rн > R,
где К и R — табличные значения критерия для соответствующих значений n.
Для того чтобы гипотезу случайности отвергнуть, достаточно наличие хотя бы одного из двух условий:
Kн ≥ K, Rн ≤ R.
Сама процедура проверки гипотезы «случайности» выборки из генеральной совокупности с непрерывным распределением заключается в следующем.
Берется выборка объема n и значения ее членов xi (например, действительных размеров) записываются в порядке извлечения экземпляров выборки. Затем определяется медиана Me наблюденного ряда значений xi и производится разбивка наблюденного ряда значений на два класса: на большие медианы и меньшие медианы. Значения xi большие или равные медиане, обозначают буквой а, значения xi меньшие медианы, буквой b. Таким образом, вся последовательность наблюденного ряда значений xi разбивается на элементы а и b, где
a = xi ≥ Me, b = xi < Me.
Составив последовательность из элементов а и b, определяют наибольшую длину серии Kн и общее число серий Rн. Затем сравнивают Kн и Rн с табличными значениями этих критериев и по результатам сравнения принимают или отвергают нулевую гипотезу. Нулевая гипотеза всегда заключается в том, что выборка предполагается «случайной».
Пример 2. С автомата, обрабатывающего ролики диаметром D =20-0,16 мм, взята текущая выборка объема n = 20. Действительные размеры роликов в порядке их изготовления имеют следующие значения: 19,89; 19,92; 19,87; 19,86; 19,89; 19,90; 19,95; 19,84; 19,90; 19,88; 19,91; 19,88; 19,93; 19,92; 19,84; 19,86; 20,0; 19,92; 19,94; 19,96.
Необходимо установить, является ли данная выборка случайной. Другими словами, выяснить, не было ли смещения центра распределения размеров в период отбора пробы.
Для проверки гипотезы случайности выборки воспользуемся критериями K и R. С этой целью сначала определим медиану наблюденного ряда значений размеров.
После расположения этого ряда в возрастающем порядке: 19,84; 19,84; 19,86; 19,86; 19,87; 19,88; 19,88; 19,89; 19,89; 19,90; 19,90; 19,91; 19,92; 19,92; 19,92; 19,93; 19,94; 19,95; 19,96; 20,00 оказалось, что Me = 19,90 мм. Теперь представим наблюденный ряд значений размеров D i в порядке изготовления роликов на станке в виде последовательности элементов a = Di ≥ Me и b = Di < Me:
b а b b b а a b a b a b a a b b a a a a.
В полученной последовательности наибольшая длина серии равна Kн = 4, а общее число серий Rн = 12. По приведенным в таблицах 2, 3 критическим значениям длины серии К и чисел серии R имеем для n = 15 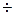 22 К = 7, а для n = 20 R = 6. Так как Kн < K и Rн > R, то наша гипотеза случайности выборки может быть принята.
22 К = 7, а для n = 20 R = 6. Так как Kн < K и Rн > R, то наша гипотеза случайности выборки может быть принята.
Дата: 2019-02-25, просмотров: 958.