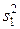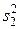Случай выборки из нормальной генеральной совокупности. Пусть имеются две выборки из нормальной совокупности. Объем каждой выборки равен n₁ и n₂. Дисперсии этих выборок соответственно равны  и . Можно ли считать при наличии некоторых различий между величинами  и , что данные выборки принадлежат одной и той же генеральной совокупности?

Или можно поставить вопрос так: произведено два опыта, из которых один опыт производился с фактором A, а другой — без него. Каждый опыт повторялся n раз. В результате обработки статистических данных получено, что дисперсия признака х в опытах с фактором A равна величине 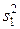, а без него - 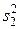. Оказывает ли существенное влияние исследуемый фактор A на признак х? Для ответа на поставленные вопросы необходимо произвести сравнение дисперсий и оценить, является ли существенным их различие.

Сравнение дисперсий производится по их отношению:

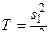                                                   (9)

В числителе всегда ставится наибольшее значение из двух наблюденных дисперсий. Для этого отношения найден закон распределения его в бесконечной совокупности случайных независимых выборок из нормальной совокупности. По этому закону вычислены значения T (в зависимости от k₁ = n₁ -1 и k₂ = n₂ - 1), которые можно встретить в выборках из нормальной совокупности для различных уровней доверительной вероятности, сведенных в таблицы. Значения Т для доверительной вероятности q = 0,05 приведены в таблице П9 приложения.

Для проверки нашей гипотезы необходимо вычислить наблюденное значение T_н = а затем определить k₁ = n₁ - 1 и k₂ = = n₂ - 1, где n₁ и n₂ — объемы выборок, и найти для этих значений k₁ и k₂ табличное значение T.

Если окажется, что наблюденное значение T_н равно или больше табличного T (T_н ≥ T), то такое значение T_н в выборках из нормальной совокупности можно встретить лишь с вероятностью не более той, которая принята в качестве доверительного уровня. Если пользоваться данными табл. П.3 приложения, то такой вероятностью является Р = 0,05. Так как эта вероятность очень мала, то по принципу практической невозможности маловероятных явлений надо считать, что наблюденное значение T_н отличается от табличного не случайно, а существенно, и поэтому наша гипотеза должна быть забракована. Если же окажется, что T_н < T, то гипотеза принимается.

Пример 5. С двух автоматов, обрабатывающих одинаковые детали, взято две выборки n₁ = n₂ = 10. При этом оказалось, что  = 400 мкм² и 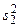 = 325 мкм². Ранее было установлено, что рассеивание размеров деталей, обработанных на автоматах, следует нормальному закону распределения.

Можно ли считать, что оба станка обеспечивают одинаковую точность обработки?

Предположим, что оба станка дают одинаковую точность и наблюденное расхождение между дисперсиями случайно. Для проверки нашей нулевой гипотезы определим критерий T_н:

T_н = 400/325 = 1,23.

По таблице П9 приложения для Р = 0,05 при k₁= k₂= 9 находим T = 3,23, следовательно, T_н < T. Поэтому надо считать нашу гипотезу верной, а наблюденное различие в значениях дисперсий выборок случайным.

Случай выборок не из нормальной совокупности. Если выборки берутся из совокупностей, незначительно отличающихся от нормальных, то для сравнения дисперсий можно пользоваться критерием T. Но, если совокупность имеет распределение, значительно отличающееся от нормального распределения, то можно сравнивать дисперсии только для больших выборок. В этом случае за критерий оценки может быть взято отношение

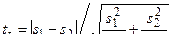.                                          (10)

Если это отношение t_s ≥ 3, то расхождение между дисперсиями существенно; если t_s < 3 — расхождение несущественно.

4. Проверка гипотезы равенства ряда дисперсий.

Пусть имеется m выборок не равных объемов n_i, взятых из одной или m генеральных совокупностей, имеющих нормальные распределения. При этом дисперсии этих совокупностей имеют одинаковые значения, т. е. 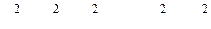, а математические ожидания могут быть и не равны друг другу.

Дисперсии выборок 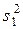, , 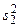,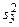…, , 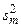вычисленные по формуле

,

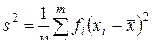несколько отличаются друг от друга по величине. Требуется проверить гипотезу о том, что это различие дисперсий выборок носит случайный характер, и, следовательно, дисперсии генеральных совокупностей , из которых взяты выборки, равны между собой, т.е. .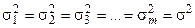

При нашей гипотезе величину

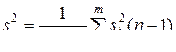,                                 (11)

где 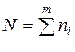, следует считать несмещенной оценкой σ². Если проверяемая гипотеза справедлива, то случайная величина

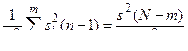
будет иметь распределение χ² с (N - m) степенями свободы.

Очевидно, что распределение отношения 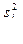 при нашей гипотезе зависит лишь от n _i.

Установлено, что случайная величина Q

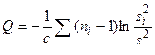,                                      (12)

где

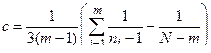
имеет распределение, близкое к распределению χ² с (m - 1) = k степенями свободы, если только n _i ≥ 3.

Для вычисления Q пользуются следующей формулой, в которой сделан переход от натуральных к десятичным логарифмам:

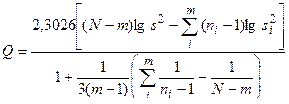.                               (13)

Задаваясь доверительным уровнем вероятности, например, q = 0,05 и пользуясь таблице П7 приложения, определяют верхний критический предел χ² при (m - 1) = k степеней свободы. Если Q < χ², то гипотеза принимается, если q > χ², то гипотеза бракуется.

Для вычисления Q рекомендуется составлять вспомогательную таблицу 3.

Таблица 3. Вспомогательная таблица для вычисления Q

№ выборки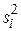

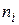
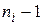
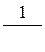
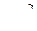
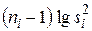
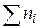
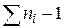
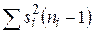
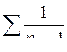
Если объемы выборок равны, т. е. n₁ = n₂ = …n_k = n, то формула (13) принимает вид

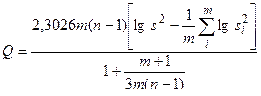,                           (14)

где s² вычисляется по формуле

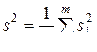                                              (15)

Однако при равном объеме выборок проверку гипотезы однородности дисперсий проще производить упрощенным приемом[3], основанным на вычислении критерия G:

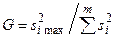.                                          (16)

Критические значения G для 5%-ного уровня значимости в зависимости от объема выборок n и числа выборок m приведены в таблице П10 приложения.

Если найденное по данным выборок G_н меньше табличного G (G_н < G), то гипотеза однородности дисперсий генеральных совокупностей, из которых были взяты выборки, принимается. Если G_н > G, то гипотеза бракуется.

Пример 6. С четырех автоматов, настроенных на обработку одних и тех же деталей, взято по одной текущей выборке объема n₁ = n₂ = n₃ = n₄ = 10. Дисперсии выборок имеют следующие значения: 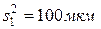, , 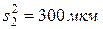, 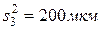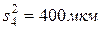. Требуется установить, одинакова ли точность автоматов, т. е. одинаково ли рассеивание случайных погрешностей обработки на этих автоматах, если предварительными исследованиями установлено, что это рассеивание подчиняется закону нормального распределения.

Для решения поставленной задачи необходимо проверить гипотезу однородности выборочных дисперсий. Проверку этой гипотезы произведем при помощи критерия Q Бартлета и критерия G. Для вычисления критерия Q по формуле (14) нужно вычислить s², lg s и .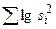

По формуле (15) имеем

;

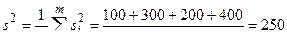lg100 = 2; lg300 = 2,48; lg200 = 2,30; lg400 = 2,60;

.

.

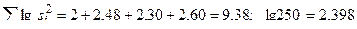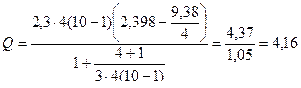По таблице П7 приложения для k = 3 и доверительной вероятности Р = 0,05 χ² = 7,8. Так как Q < c², то гипотеза однородности дисперсии принимается, т. е. наблюденные значения 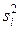отличаются друг от друга случайно. Это подтверждается и критерием G:

.

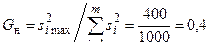По таблице П10 приложения для доверительной вероятности q = 5%

G = 0,5. Так как G_н < G, то гипотеза подтверждается.