Статистический анализ методом большой выборки производится после того, как станок проработает некоторое время (в пределах одного-двух часов), необходимое для стабилизации температуры системы СПИД. За это время погрешности обработки, вызываемые температурными деформациями элементов системы СПИД, превратятся из функциональных погрешностей в постоянные погрешности, и процесс обработки при нормальном его ходе будет характеризоваться диаграммой точности I или IV типа.

Статистический анализ точности механической обработки посредством большой выборки включает в себя выполнение следующих процедур.

7. Взятие из текущей продукции станка большой выборки. Выборка должна состоять из деталей, изготовленных подряд одна за другой при неизменной настройке станка и других неизменных условиях. Объем выборки устанавливается в зависимости от желаемой точности и надежности определения меры рассеивания σ суммарной погрешности обработки. Для этого используются методики, изложенные в темах 4, 5. Для практических целей можно принять точность вычисления оценки σ по выборочному s, равную ε = ±0,2s с вероятностью α = 0,95. Тогда объем выборки достаточно сделать равным n = 50. Однако с увеличением n точность ε возрастает, и поэтому часто принимают n ≥ 100.

1. Измерение всех деталей выборки шкальным измерительным инструментом. Цена деления измерительной шкалы инструмента должна быть равной 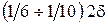, где 2δ —допуск на измеряемый размер. Результаты заносятся в таблицу в последовательности измерения очередной детали.

2. Вычисление статистических характеристик выборки 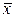и s . Характеристики выборки 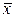и s в дальнейшем принимаются в качестве оценок параметров  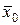и σ₀ распределения генеральной совокупности, из которой взята выборка.

3. Проверка гипотезы о случайности выборки. Эта проверка позволяет установить наличие или отсутствие функциональных погрешностей обработки, обуславливающих смещение центра рассеивания (статистики ).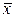

При наблюдениях изменений размеров обрабатываемых деталей на настроенном станке проверку гипотезы случайности выборки обычно осуществляют методом последовательных разностей.

4. Проверка гипотезы о нормальности распределения. Поскольку берется выборка большого объема, то проверку гипотезы о нормальном распределении генеральной совокупности по взятой из нее выборке выполняют по критерию l (см. тему 4).

5. Определение, к какому типу точности может быть отнесен рассматриваемый процесс механической обработки деталей? При положительных результатах проверки гипотез случайности выборки и нормальности распределения процесс может быть отнесен к IV типу точности и определена погрешность обработки.

Если при проверке случайности и нормальности распределения по большой выборке получены отрицательные результаты, то проводят исследования по определению, является или нет изучаемый процесс технологически устойчивым.

Для этого выполняют следующие операции.

· Взятую большую выборку разбивают в порядке изготовления деталей на m групп по n штук в каждой группе. Число n выбирается в зависимости от объема выборки и машинного времени обработки детали. Обычно принимают n = 5, но для мелких деталей с очень малым машинным временем обработки можно принимать n ≥ 10, но так, чтобы число групп m было не менее 10.

Группу деталей из n штук можно рассматривать как выборку из «мгновенной» совокупности, имеющей нормальное распределение, так как за время изготовления n штук деталей функциональные погрешности будут иметь пренебрежимо малые значения и, следовательно, будут иметь место только случайные погрешности.

· Для каждой группы вычисляют среднее значение действительных отклонений размеров от номинала 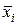 и дисперсию 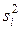. Каждую группу (особенно, когда n > 5) проверяют на случайность по методу последовательных разностей. Если гипотеза случайности не подтвердится, то уменьшают число n деталей в группе.

· Для оценки статистической устойчивости процесса по рассеиванию проверяют гипотезу однородности групповых дисперсий 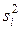 по критерию 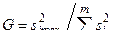, если 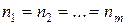, или по критерию 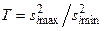. При положительных результатах проверки этой гипотезы переходят к определению наличия и вида связи групповых средних  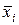с временем  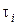изготовления групп деталей или с номерами групп, приняв , , …, .

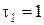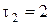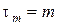· Определение наличия и вида связи групповых средних 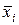 с временем  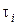изготовления групп деталей осуществляют путем построения графика зависимости  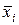от τ_i в системе координат  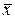- τ.

Если по виду построенного графика может быть выдвинута гипотеза о линейной зависимости групповых средних 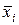 от времени 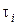, то регрессионным анализом определяют коэффициенты а и b уравнения  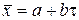этой зависимости.

· Проверка гипотезы о линейной связи между 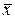 и τ. Эта проверка включает в себя:

1) вычисление оценки 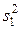 дисперсии  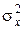распределения генеральной совокупности случайных величин x_i по формуле

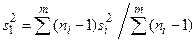
или по формуле

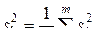, если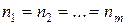

и оценки 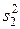 дисперсии  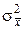рассеивания эмпирических значений  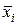относительно теоретических 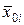, определяемых уравнением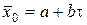

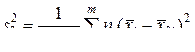
2) вычисление критерия значимости 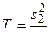 и сравнение его с критическим значением T, приведенным в таблице П9 приложения. При использовании этой таблицы учитывают, что  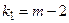и .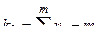

Если полученное значение T будет меньше табличного значения T_т, то гипотеза о линейности связи 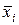 с τ принимается. В противном случае гипотеза отвергается.

Если гипотеза подтвердится, то процесс можно считать технологически устойчивым и отнести его к I типу точности.

Необходимо заметить, что при проверке гипотез равенства групповых дисперсий и гипотезы линейности связи 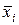 с τ, не следует предъявлять жестких требований к критериям значимости. Практически можно считать процесс технологически устойчивым, если однородность групповых дисперсий и линейность связи между  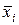и τ подтверждаются критериями G и T при доверительном уровне значимости их, равном q = 0,1, а не 0,05. Если в результате регрессионного анализа линейность связи  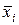с τ не подтвердится, то процесс нельзя считать устойчивым во времени и необходимо выяснить причины его неустойчивости, устранить их и после этого повторить статистический анализ.

Если в результате анализа будет установлено, что изучаемый процесс является технологически устойчивым, то для оценки его точности нужно знать, к какому типу точности он относится не после стабилизации теплового режима системы СПИД, а с момента пуска станка.

Для этого необходимо взять большую выборку сразу же после наладки и пуска станка и провести статистический анализ точности обработки.