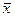Предположим, что из одной и той же генеральной совокупности взяты две выборки, которые для величины х дают средние 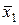 и
и 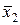 , отличные одна от другой. Требуется узнать, случайно или не случайно они отличаются друг от друга. Этот вопрос имеет важное значение при проведении опытов. Если расхождение между
, отличные одна от другой. Требуется узнать, случайно или не случайно они отличаются друг от друга. Этот вопрос имеет важное значение при проведении опытов. Если расхождение между 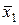 и
и 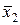 , будет существенно, то это может указать на ошибки в опытах или в методике их выполнения, тогда как случайность их расхождения указывает на отсутствие таких ошибок.
, будет существенно, то это может указать на ошибки в опытах или в методике их выполнения, тогда как случайность их расхождения указывает на отсутствие таких ошибок.
Подобный вопрос возникает и при исследовании влияния различных факторов на изучаемый признак. Пусть опыты с фактором A и без него дали отличные друг от друга 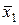 и
и 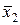 . Является очевидным, что при случайном отличии значений
. Является очевидным, что при случайном отличии значений 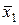 и
и 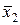 фактор A не влияет на исследуемый признак и, наоборот, влияет при существенном расхождении между
фактор A не влияет на исследуемый признак и, наоборот, влияет при существенном расхождении между 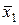 и
и 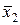 . Возможен на практике и такой вопрос, принадлежат ли две выборки одной и той же генеральной совокупности. Этот вопрос также можно разрешить, сравнивая выборочные средние
. Возможен на практике и такой вопрос, принадлежат ли две выборки одной и той же генеральной совокупности. Этот вопрос также можно разрешить, сравнивая выборочные средние 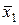 и
и 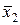 и оценивая их расхождение.
и оценивая их расхождение.
Отметим, что если выборки взяты из одной и той же генеральной совокупности, то расхождение между 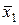 и
и 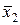 будет случайным, и, наоборот, оно будет существенным, когда выборки не будут принадлежать одной и той же совокупности.
будет случайным, и, наоборот, оно будет существенным, когда выборки не будут принадлежать одной и той же совокупности.
Рассмотрим два возможных случая:
1) выборки берутся из нормальной генеральной совокупности;
2) выборки берутся из совокупности, которая не подчиняется закону нормального распределения или когда закон распределения генеральной совокупности неизвестен.
Случай выборки из нормальной генеральной совокупности. В этом случае оценка расхождения двух выборочных средних производится при помощи критерия t Стьюдента. Если выборки берутся из нормальной совокупности, то величина
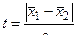 (4)
(4)
подчинена распределению Стьюдента и может быть оценена при помощи таблицы вероятностей 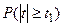 (таблица П8 приложения).
(таблица П8 приложения).
В выражении (4) 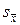 – вычисляется по формуле
– вычисляется по формуле
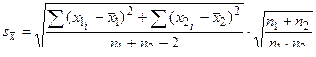 . (5)
. (5)
Принимая во внимание, что
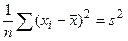 и
и 
выражение (5) можно заменить следующим:
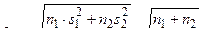 . (6)
. (6)
Подставляя значение 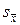 из выражения (6) в формулу (4), окончательно получим
из выражения (6) в формулу (4), окончательно получим
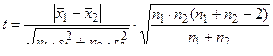 , (7)
, (7)
где 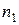 и
и 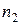 – объем выборок;
– объем выборок; 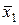 и
и 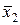 ;
; 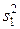 и
и 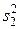 — их средние и дисперсии.
— их средние и дисперсии.
При оценке полученного значения t по таблице П8 приложения необходимо принимать 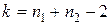 . Таблица
. Таблица 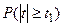 дает вероятность случайных значений t, которые численно не менее наблюденного значения t1. Если эта вероятность будет очень мала (практически, когда P ≤ 0,05), то наша нулевая гипотеза о несущественном, случайном расхождении между выборочными средними должна быть забракована. Если же вероятность
дает вероятность случайных значений t, которые численно не менее наблюденного значения t1. Если эта вероятность будет очень мала (практически, когда P ≤ 0,05), то наша нулевая гипотеза о несущественном, случайном расхождении между выборочными средними должна быть забракована. Если же вероятность 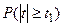 будет достаточно велика (практически, когда P > 0,05), то гипотеза однородности выборочных средних может быть принята.
будет достаточно велика (практически, когда P > 0,05), то гипотеза однородности выборочных средних может быть принята.
Рассмотренный метод сравнения и оценки расхождения выборочных средних пригоден для малых выборок, когда объем их n < 25. При этом необходимо отметить, что применение критерия связано с предположением о равенстве дисперсий выборок. Это последнее допущение должно быть предварительно обосновано. В противном случае показания критерия t могут привести к ошибочным заключениям.
Если объем выборок n > 25, то критерий t вычисляется по формуле
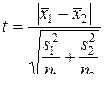 (8)
(8)
Пример 3. С автомата, обрабатывающего втулки D =20+0,2 мм, было взято в разное время две выборки по 5 шт. каждая. Результаты измерения диаметров втулок приведены в таблице 4. Распределение диаметров втулок предполагается нормальным.
Таблица 4. Результаты измерения диаметра втулок
| № выборки | № детали |
|
| ||||
| 1 | 2 | 3 | 4 | 5 | |||
| Выборка 1 | 20,05 | 20,08 | 20,10 | 20,10 | 20,09 | 20,084 | 0,0004 |
| Выборка 2 | 20,10 | 20,15 | 20,05 | 20,08 | 20,10 | 20,096 | 0,0013 |
Поскольку выборки взяты из продукции одного и того же станка, можно предполагать, что 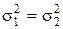 . Пусть наша гипотеза заключается в том, что генеральные средние в моменты взятия выборок были равны между собой, т. е.
. Пусть наша гипотеза заключается в том, что генеральные средние в моменты взятия выборок были равны между собой, т. е. 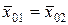 . Другими словами, настройка станка в момент взятия пробы № 1 и № 2 не изменилась.
. Другими словами, настройка станка в момент взятия пробы № 1 и № 2 не изменилась.
В результате вычислений средних арифметических и дисперсий выборок получено
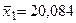 ;
; 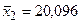 ;
; 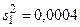 ;
; 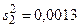 .
.
Определим t:
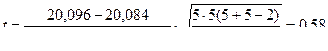 .
.
Из таблицы П8 приложения находим, что при k = 5 + 5 – 2 = 8 вероятность 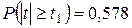 . Эта вероятность не мала, она значительно больше доверительного уровня P = 0,05, поэтому наша гипотеза может быть принята.
. Эта вероятность не мала, она значительно больше доверительного уровня P = 0,05, поэтому наша гипотеза может быть принята.
Пример 4. При одних и тех же условиях было обработано по 25 шт. втулок разверткой d = 6 мм и разверткой d = 10 мм. Результаты измерений двух партий втулок показали, что средняя величина разбивки отверстий (разность между диаметром отверстия и диаметром развертки) составляет для d = 6 мм 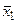 = 10,4 мкм, для d = 10 мм
= 10,4 мкм, для d = 10 мм 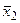 = 9,8 мкм. Дисперсии величин разбивки отверстий соответственно равны:
= 9,8 мкм. Дисперсии величин разбивки отверстий соответственно равны:  = 3,8 мкм2;
= 3,8 мкм2;  = 4,76 мкм2.
= 4,76 мкм2.
Необходимо установить, влияет ли диаметр развертки на величину разбивки отверстий, если предварительными опытами установлено, что рассеивание величин разбивки подчиняется нормальному закону распределения.
Наша нулевая гипотеза будет состоять в том, что размер развертки не влияет на величину разбивки отверстий.
Вычислим величину t по формуле (8): 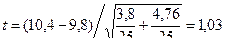 .
.
По таблице П8 приложения этому значению t соответствует Р = 0,31. Эта вероятность не мала, следовательно, наша нулевая гипотеза верна, т. е. можно считать, что размер развертки в пределах от d = 6 мм до d = 10 мм не оказывает существенного влияния на величину разбивки отверстий.
Случай выборок не из нормальной совокупности. Если выборка взята из генеральной совокупности, распределение которой не следует закону нормального распределения, то оценка расхождения двух выборочных средних возможна лишь приближенная.
Для этой цели также определяется величина t, причем t вычисляется так же, как и в предыдущем случае по формуле (7) или (8) в зависимости от объема выборок.
Если окажется, что t ≥ 3, то с большой вероятностью (которая, однако, остается неопределенной) можно считать, что средние 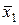 и
и 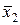 различаются существенно друг от друга и, наоборот, при t < 3 расхождение между
различаются существенно друг от друга и, наоборот, при t < 3 расхождение между 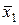 и
и 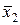 с большой вероятностью можно считать несущественным, случайным.
с большой вероятностью можно считать несущественным, случайным.
Дата: 2019-02-25, просмотров: 391.