Всякая статистическая оценка параметра, вычисленная по данным выборки, может быть только приближенной. Поэтому она имеет определенный смысл лишь в том случае, когда указываются границы возможной погрешности оценки, т. е. указывается интервал, внутри которого с заданной вероятностью будет лежать истинное значение параметра. Этот интервал носит название доверительного, а его границы – доверительных границ.

Доверительные границы для среднего значения , дисперсии  и среднего квадратического отклонения σ₀ в случае нормальной генеральной совокупности определяются следующим образом.

Доверительные интервалы для оценки генеральной средней . Если генеральная совокупность имеет нормальное распределение, то, как было указано ранее, величина 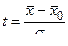 для больших выборок также распределена нормально со средним значением  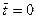и дисперсией 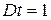. Поэтому для любого уровня значимости P легко построить доверительные границы для неизвестного значения , воспользовавшись неравенством:

,

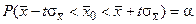подставляя в которое 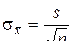, получим

.

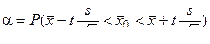Величина t определяется по таблице П1 приложения по заданной вероятности α = 2Ф(t). Например, для n = 100 и надежности α = 0,95  t = 1,96., поэтому доверительный интервал будет иметь начальную точку 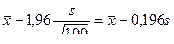 и конечную точку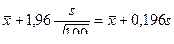  

Следовательно, неизвестное среднее значение  с вероятностью 0,95 будет находиться внутри интервала .

Значения 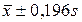 являются доверительными границами для среднего значения генеральной совокупности при 5%-ном уровне значимости. Уровень значимости равен q = 1 - α = 1 - 0,95 = 0,05.

Если выборка имеет объем n ≤ 25, то величина t имеет распределение Стьюдента. Поэтому в этом случае значение t определяется по таблице П2 приложения по заданному значению α и k = n - 1.

Например, для n = 10 и α = 0,95 по таблице П2 приложения имеем 2t = 2,26. Поэтому доверительные границы для  будут равны

.

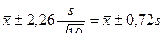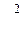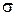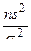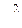Определение доверительных интервалов для оценки генеральных величин  и . Если генеральная совокупность имеет нормальное распределение, то величина  имеет -распределение с числом степеней свободы k = n - 1. Здесь n - объем выборки и s² - дисперсия выборки.

Задавшись вероятностью α при определении доверительных границ для 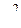 и определив доверительный уровень значимости q = 1 - α, можно вычислить по 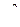-распределению величины  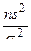два значения 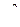: одно для вероятности P₁ = 1-q/2 обозначим его  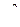и другое для вероятности P₂ = q/2, обозначим его - 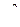.  Тогда вероятность того, что величина  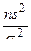окажется в границах от  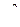до 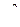, будет равна α:

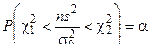                                     (17)

или с той же вероятностью можно ожидать выполнение следующих неравенств:

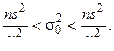
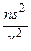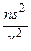Два числа  и  определяют доверительные границы для 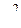. Значения  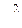для различных вероятностей P приведены в таблице П6 приложения.

Например, при доверительной вероятности α = 0,96 и q = 1 - α = 0,04 для выборки n = 20 по таблице П4 приложения имеем:

для k = n - 1 = 20 - 1 = 19 и P₁ = 1 - q/2 = 1 - 0,02 = 0,98 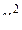 = 8,64; для P₂ = q/2 = 0,02  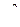= 33,7; следовательно, доверительные границы для  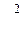будут равны

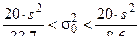или .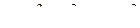

Оценка для параметра 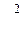 с помощью доверительного интервала  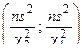дает в то же время доверительный интервал  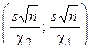для оценки параметра σ₀ с той же доверительной вероятностью α.

Обозначим 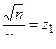 и 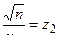. Тогда

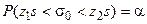.                                (18)

Значения z₁ и z₂ для доверительной вероятности α = 0,95 приведены в таблице П5 приложения.

Для больших выборок можно использовать неравенство (13)

,

которое после замены 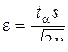 примет вид

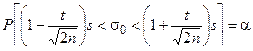.                  (19)

Задавшись α = 2Ф(t), по таблице П1 приложения определяем t и по полученному t вычисляем доверительные границы σ₀. Например, n = 100,

α = 0,95. По таблице П1 приложения t = 1,96, следовательно,

;

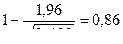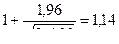
и доверительные границы с вероятностью α = 0,95 составляют

0,86s <σ₀< 1,14s.

Контрольные вопросы

1. Поясните термины: «генеральная совокупность», «выборка», «репрезентативная выборка».

2. Какие задачи решают выборочным методом, исследуя распределение случайной величины?

3. В чем отличие между повторными и бесповторными выборками? Дайте краткие определения следующих выборок: преднамеренные, случайные, мгновенные, общие, малые, большие.

4. Поясните требования к оценкам параметров генеральной совокупности, например, оценок 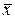 и s соответствующих параметров  и σ₀ генеральной совокупности: «они должны быть состоятельными, несмещенными и эффективными».

5. По выборке объема n < 20 найдены значения 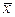 и s. Приведите последовательность процедур определения доверительного интервала, в котором находится истинное значение генеральной средней .

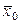6. Приведите последовательность операций определения объема n выборки, необходимого для вычисления по этой выборке генеральной средней с точностью  и вероятностью α = 0,95.

7. Как можно определить по заданной вероятности α, объеме выборки п и среднего квадратического отклонения s выборки точность оценки σ₀ генеральной совокупности?

Лекция 4