О законе распределения случайной величины

Статистическая гипотеза. Основные понятия

Статистическая проверка гипотез, т. е. предположений, относящихся к эмпирическим распределениям изучаемых случайных величин, играет важную роль в исследованиях процессов механической обработки деталей.

Если эмпирическая кривая распределения большой выборки по своему внешнему виду приближается к какому-либо теоретическому закону распре­деления, то возникает вопрос, можно ли данную выборку рассматривать как выборку из генеральной совокупности, имеющей распределение именно по этому закону. Решение этого вопроса имеет большое значение для исследователя, так как знание закона распределения изучаемой величины позволяет извлечь из экспериментов дополнительную информацию. Еще пример, если производится две серии испытаний с фактором A и без него и в результате получаются разные значения средних и дисперсий изучаемой переменной величины, то возникает вопрос, является ли это различие в средних и дисперсиях влиянием фактора A или оно носит чисто случайный характер. В математической статистике подобные задачи относятся к задачам проверки статистических гипотез.

Статистическая гипотеза – это содержательное высказывание о свойствах генеральной совокупности, исходя из свойств выборки x₁, x₂,…, x_n из этой генеральной совокупности.

Статистические гипотезы делятся на:

· параметрические – гипотезы, сформулированные относительно параметров распределения известного вида (среднего арифметического значения, дисперсии и т. п.);

· непараметрические - гипотезы, сформулированные относительно вида распределения, например, предположение по распределению данных выборки о нормальном законе генеральной совокупности.

В математической статистике процесс проверки гипотезы включает в себя постановку и определение достоверности основной, так называемой «нулевой гипотезы» H₀. Постановка «нулевой гипотезы» заключается в формулировке допущения об отсутствии интересующего нас различия между выборкой и ее генеральной совокупностью. Например, нас интересует, можно ли по полученному распределению в большой выборке из генеральной совокупности считать, что последняя имеет нормальное распределение. Для того чтобы прийти к вполне определенному заключению, хотя бы и вероятностного характера, мы делаем гипотетическое допущение, что распределение выборки несущественно отличается от нормального и, следовательно, на основании закона больших чисел можно считать, что и генеральная совокупность имеет нормальное распределение. Другими словами, мы выдвигаем «нулевую гипотезу» H₀: данная выборка взята из нормальной совокупности.

Наряду с нулевой гипотезой H₀ рассматривается альтернативная ей гипотеза H₁. Для выше приведенной нулевой гипотезы H₀ альтернативная ей гипотеза может быть сформулирована как H₁: данная выборка не принадлежит нормальной совокупности. Далее осуществляется проверка этих гипотез.

Проверка нуль – гипотезы производится с использованием различных статистических критериев, позволяющих с помощью их уровней значимости q сделать вывод об опровержении гипотезы H₀ и принятии альтернативной ей гипотезы H₁.

Статистическим критерием K называют случайную величину, с помощью которой принимают решение о принятии или отклонении нуль - гипотезы H₀. Различают критерии значимости и критерии согласия. Критерии значимости используются для проверки гипотез о параметрах распределения генеральной совокупности (проверки параметрических гипотез). К ним относятся критерии Стьюдента, Фишера и др.

Критерии согласия применяют для проверки гипотез о законах статистических распределений. Из этих критериев широко используются критерий λ А. Н. Колмогорова и критерий 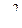 К. Пирсона.

Уровень значимости q критерия K представляет собой достаточно малое значение вероятности, отвечающее событиям, которые в данной обстановке исследования можно считать практически невозможными. Обычно принимают пяти- двух- или однопроцентный уровень значимости. В технике чаще всего принимают пятипроцентный уровень значимости. Эти уровни значимости соответствуют классификации явлений на редкие (q = 0,05), очень редкие (q = 0,01) и чрезвычайно редкие (q = 0,001). Выбирая тот или иной уровень значимости q критерия K, мы тем самым устанавливаем и область допустимых его значений, при которых выдвинутая гипотеза считается достоверной.

Статистические приемы проверки гипотез не обладают полной определенностью. Если используемый критерий попадает в область допустимых значений, то нельзя еще сделать вывод о правильности гипотезы. Пока можно лишь заключить, что наблюденное значение критерия не противоречит этой гипотезе, что можно признать допустимость гипотезы до тех пор, пока более обстоятельные исследования с помощью более точных критериев или при увеличенном числе наблюдений не подтвердят это или не приведут к противоположному заключению. Поэтому статистическими методами нельзя пользоваться формально, а необходимо их сочетать с анализом физической сущности изучаемого явления. Когда гипотеза, основанная на теоретическом анализе физической сущности явления, подтверждается также статистическими приемами, то достоверность ее можно считать достаточно надежной.

В статистических исследованиях процессов механической обработки деталей наиболее часто проверяют гипотезы:

· о законе распределения случайной величины (точности обработки, шероховатости поверхности, стойкости инструмента и др.);

· случайности выборки;

· равенства двух выборочных средних;

· равенства двух и более дисперсий;

· о принадлежности двух выборок одной и той же генеральной совокупности.

Последовательность проверки гипотез включает следующие операции:

- формулируется «нулевая гипотеза»;

- выбирается уровень значимости;

- выбирается критерий согласия и определяется его критическое значение (по соответствующей таблице математической статистики);

- вычисляется по результатам выборки расчетное (выборочное) значение критерия согласия;

- принимается или отвергается нуль-гипотеза.