Подавляющее число показателей, являющихся количественными характеристиками свойств различных технологических процессов, режущих инструментов, отдельных деталей и машин, относятся к случайным величинам. Наиболее полной характеристикой любой случайной величины является ее закон распределения, устанавливающий связь между возможными значениями случайной величины и соответствующими им вероятностями. Поэтому установление закона распределения исследуемой случайной величины, например, точности обработки, стойкости режущего инструмента, долговечности изделия и др., является одной из важных задач статистической обработки данных. Следует заметить, что результаты решения этой задачи предопределяют успех тех или иных мероприятий, осуществляемых по управлению точностью и стабильностью отдельных процессов изготовления изделий и управлению качеством выпускаемой продукции в целом.
Является очевидным, что в любом статистическом распределении неизбежно присутствуют в той или иной степени элементы случайности. Их наличие обусловлено ограниченным числом наблюдений, выполнением именно тех, а не других опытов, давших именно эти, а не другие результаты и т. п. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает в полной мере присущую ему закономерность. Однако на практике всегда имеют дело с ограниченным объемом данных и, как следствие, необходимостью учета имеющихся в рассматриваемом статистическом распределении в большей или меньшей степени черт случайности. Поэтому при обработке статистических данных приходится решать вопрос, как подобрать для полученных статистических данных теоретическую кривую распределения, отражающую лишь существенные черты распределения исследуемой величины, а не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.
В общем случае постановка задачи выравнивания статистического ряда может иметь следующий вид.
Пусть изучается некоторая случайная величина X, закон распределения которой в точности не известен. Над случайной величиной X выполнен ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина X принимало определенное значение.
Выдвинуть на основании статистической совокупности наблюденных в выборке значений случайной величины X гипотезу овозможном законе ее распределения.
Следует заметить, что для установления закона распределения случайной величины X стремятся получить достаточно большую выборку, содержащей порядка 50 - 100 и более результатов наблюдений. Совокупность наблюденных значений величины X представляет первичный статистический материал, подлежащий обработке, осмыслению и научному анализу. Такую совокупность принято называть простой статистической совокупностью или простым статистическим рядом.
Обычно простая статистическая совокупность оформляется в виде таблицы с одним входом, в первом столбце которой стоит номер опыта, а во втором – наблюденное значение случайной величины. Нередко статистическая совокупность оформляется в виде таблицы, содержащей только значения случайной величины. В этом случае номер опыта предопределяется порядком расположения этих значений в таблице, как это следует из нижеприведенного примера.
Методику выравнивания статистического распределения изучаемой случайной величины X рассмотрим на следующем примере.
Пример 1. С целью определения закона распределения погрешности обработки из текущей продукции автомата, обрабатывающего ролики D = 20-0,2 мм, взята выборка объемом n = 100 шт. Ролики были измерены по диаметру микрометром с ценой деления 0,01 мм. Результаты измерений сведены в таблицу 1 в виде значений отклонения от номинального размера диаметра роликов в мм.
Таблица 1. Отклонения xi от номинального размера диаметра D роликов в мм. (простая статистическая совокупность)
| -0,07 | -0,03 | -0,04 | -0,08 | -0,03 | -0,08 | -0,09 | -0,10 | -0,10 | -0,10 |
| -0,13 | -0,08 | -0,06 | -0,04 | -0,04 | -0,03 | -0,04 | -0,07 | -0,11 | -0,12 |
| -0,03 | -0,07 | -0,08 | -0,11 | -0,05 | -0,05 | -0,07 | -0,03 | -0,09 | -0,10 |
| -0,11 | -0,14 | -0,13 | -0,08 | -0,12 | -0,07 | -0,09 | -0,10 | -0,11 | -0,08 |
| -0,05 | -0,12 | -0,07 | -0,06 | -0,08 | -0,11 | -0,10 | -0,12 | -0,03 | -0,10 |
| -0,08 | -0,05 | -0,11 | -0,07 | -0,05 | -0,08 | -0,09 | -0,09 | -0,09 | -0,02 |
| -0,06 | -0,12 | -0,05 | -0,07 | -0,11 | -0,05 | -0,08 | -0,03 | -0,11 | -0,09 |
| -0,11 | -0,06 | -0,07 | -0,06 | -0,06 | -0,12 | -0,10 | -0,08 | -0,09 | -0,01 |
| -0,05 | -0,07 | -0,06 | -0,05 | -0,08 | -0,09 | -0,04 | -0,09 | -0,08 | -0,09 |
| -0,07 | -0,06 | -0,06 | -0,12 | -0,05 | -0,03 | -0,10 | -0,09 | -0,09 | -0,08 |
Легко заметить из таблицы 1, что оформление статистического материала в виде простой статистической совокупности затрудняет решение задачи выравнивания статистического ряда, поскольку не дает какое-либо представление о характере изменения случайной величины. Особенно это проявляется при большом числе наблюдений (порядка сотни и более значений), когда простая статистическая совокупность становится неудобной, громоздкой и мало наглядной формой записи статистического материала для определения закона распределения случайной величины.
Для придания статистическому материалу компактности и наглядности его подвергают дополнительной обработке - построению так называемого статистического ряда.
Статистический ряд представляет собой таблицу, содержащую определенное число интервалов, на которые разбит диапазон предварительно ранжированных в порядке возрастания наблюденных значений случайной величины. Число таких интервалов должно быть не менее 6-7 при n = 50-100 и не менее 9—15 при n > 100. Величина интервала должна быть больше величины деления шкалы измерительного инструмента, которым производился обмер величины X в выборке, для того чтобы можно было этим компенсировать погрешности измерения.
Для каждого интервала приводится количество значений случайной величины (частота), принадлежащих соответствующему интервалу.
Так, для случайной величины X (погрешности обработки роликов), рассматриваемой в примере 1, в результате ранжирования ее значений в порядке их возрастания, получим распределение, приведенное в таблице 2.
Согласно данным таблицы 2, наибольшее наблюденное значение xmax = =– 0,01, наименьшее xmin = – 0,14. Размах распределения данных составляет
 .
.
Таблица 2. Ранжированные значения отклонения диаметра роликов от номинального размера в мм.
| -0,14 | -0,11 | -0,1 | -0,09 | -0,09 | -0,08 | -0,07 | -0,06 | -0,05 | -0,03 |
| -0,13 | -0,11 | -0,1 | -0,09 | -0,08 | -0,08 | -0,07 | -0,06 | -0,05 | -0,03 |
| -0,13 | -0,11 | -0,1 | -0,09 | -0,08 | -0,08 | -0,07 | -0,06 | -0,05 | -0,03 |
| -0,12 | -0,11 | -0,1 | -0,09 | -0,08 | -0,08 | -0,07 | -0,06 | -0,05 | -0,03 |
| -0,12 | -0,11 | -0,1 | -0,09 | -0,08 | -0,08 | -0,07 | -0,06 | -0,05 | -0,03 |
| -0,12 | -0,11 | -0,1 | -0,09 | -0,08 | -0,07 | -0,07 | -0,05 | -0,04 | -0,03 |
| -0,12 | -0,11 | -0,1 | -0,09 | -0,08 | -0,07 | -0,06 | -0,05 | -0,04 | -0,03 |
| -0,12 | -0,11 | -0,1 | -0,09 | -0,08 | -0,07 | -0,06 | -0,05 | -0,04 | -0,03 |
| -0,12 | -0,11 | -0,09 | -0,09 | -0,08 | -0,07 | -0,06 | -0,05 | -0,04 | -0,02 |
| -0,12 | -0,1 | -0,09 | -0,09 | -0,08 | -0,07 | -0,06 | -0,05 | -0,04 | -0,01 |
Согласно данным таблицы 2, наибольшее наблюденное значение xmax = =– 0,01, наименьшее xmin = – 0,14. Размах распределения данных составляет
 .
.
Принимая число интервалов, равным 7, находим цену интервала l = 0,13/7 » 0,02 мм. Полученная величина интервала в два раза больше цены деления шкалы измерительного инструмента, что вполне приемлемо.
Выполнив подсчет частот по каждому интервалу, получим статистический ряд (таблица 3), отражающий эмпирическое распределение исследуемой случайной величины (погрешности обработки роликов).
Таблица 3. Эмпирическое распределение х (статистический ряд)
| Интервалы х | Середина интервала | Частота f | Частость | |
| от | до | |||
| -0,14 | -0,12 | -0,13 | 3 | 0,03 |
| -0,12 | -0,10 | -0,11 | 16 | 0,16 |
| -0,10 | -0,08 | -0,09 | 22 | 0,22 |
| -0,08 | -0,06 | -0,07 | 25 | 0,25 |
| -0,06 | -0,04 | -0,05 | 19 | 0,19 |
| -0,04 | -0,02 | -0,03 | 13 | 0,13 |
| -0,02 | -0,00 | -0,01 | 2 | 0,02 |
|
| 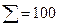
| 
| ||
Дополнительно в таблице приведены значения относительной частоты, называемой частостью. Она вычисляется как отношение частоты значений случайной величины, принадлежащих соответствующему интервалу к общему количеству наблюденных значений случайной величины, т. е. является статистической вероятностью возникновения значения случайной величины в данном интервале диапазона наблюденных значений. Является очевидным, что сумма частостей всех интервалов должна быть равна единице.
 Статистический ряд позволяет представить опытные данные графически в виде гистограммы или полигона (рис. 4), визуальный анализ которых помогает в определенной степени установить закон распределения исследуемой случайной величины.
Статистический ряд позволяет представить опытные данные графически в виде гистограммы или полигона (рис. 4), визуальный анализ которых помогает в определенной степени установить закон распределения исследуемой случайной величины.
Для определения закона распределения случайной величины существуют два подхода. Первый подход основан на подборе, исходя из внешнего вида статистического распределения, наиболее подходящей функции для его аналитического описания. В принципе выравнивание статистического ряда можно осуществить с помощью любой аналитической функции, обладающей основными свойствами плотности распределения φ(x):
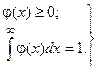 (1)
(1)
Такой подход выбора закона распределения обладает существенным недостатком, а именно, выбранная функция в качестве закона статистического распределения не отражает физическую сущность исследуемого объекта.
Определение закона статистического распределения при втором подходе осуществляется путем выбора теоретической кривой из существующих в теории вероятностей и математической статистике теоретических распределений. Основанием такого подхода служит то, что разработанные в теории вероятностей и математической статистике теоретические законы распределения имеют своим источником реальные процессы и получены логическим путем с использованием физических характеристик этих процессов. Это позволяет выполнить выбор вида теоретической кривой не по внешним формальным признакам, а по близости (общности) физической сущности рассматриваемого случайного процесса и выбираемого теоретического закона распределения[2]. В данном случае обеспечивается выбор теоретического закона, аналитическое выражение которого содержит параметры, характеризующие физическую сущность исследуемого случайного процесса или явления. При этом задача выравнивания статистического ряда переходит в задачу рационального выбора таких значений параметров закона распределения, при которых соответствие между статистическим и теоретическим распределением оказывается наилучшим.
Так, исследуемая в примере 1 случайная величина X есть погрешность размера деталей, обработанных на станке, настроенном на заданный размер детали. Эта погрешность обработки обусловлена действием множества случайных независимых факторов (вариации твердости материала заготовок детали, колебанием размера заготовок и т. д.). Из анализа результатов, представленных в виде статистического ряда (табл. 3) и теоретических соображений можно считать, что распределение величины X подчиняется нормальному закону:
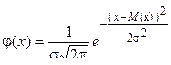 . (2)
. (2)
Таким образом, задача выравнивания статистического ряда переходит в задачу о рациональном выборе параметров M(x) и σ в выражении (2). Обычно принимают, что параметры выбранного теоретического закона распределения равны соответствующим статистическим параметрам исследуемой величины X. В частности, для приведенного закона (2) принимают, что
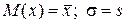 . (3)
. (3)
Построив с использованием условий (3) теоретическую кривую распределения и сопоставив ее со статическим распределением, представленным, например, в виде гистограммы, можно визуально оценить близость теоретического и статического распределения.
Выполним отмеченные операции выравнивания статистического ряда, используя данные таблицы 3 эмпирического распределения погрешности обработки роликов.
Вычисление статистических характеристик предполагаемого закона нормального распределения
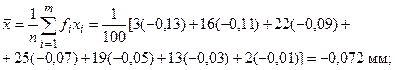
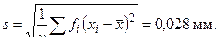
Определение значений теоретических частот 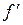 нормального закона распределения погрешности обработки роликов. Принимая параметры
нормального закона распределения погрешности обработки роликов. Принимая параметры 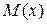 и
и 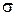 закона (2) равными статистическим характеристикам выборки, т. е.
закона (2) равными статистическим характеристикам выборки, т. е. 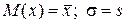 , выражение нормального закона, выравнивающего статистическое распределение примет вид:
, выражение нормального закона, выравнивающего статистическое распределение примет вид:
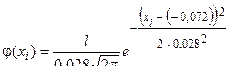 . (4)
. (4)
где l - цена единичного интервала размаха распределения величины x.
Вычислив теоретические частоты по уравнению (4), получим результаты, приведенные в таблице 4.
Визуальная о ценка близости эмпирического распределения к предполагаемому теоретическому закону. На рис. 5 приведены полученные теоретическая и эмпирическая кривые распределения.
Таблица 4. Результаты вычисления теоретических частот нормального распределения
| Интервалы x | Середина интервала xi |
|
|
| |
| от | до | ||||
| -0,18 | -0,16 | -0,17 | 0 | 0,062 | 0 |
| -0,16 | -0,14 | -0,15 | 0 | 0,588 | 1 |
| -0,14 | -0,12 | -0,13 | 3 | 3,335 | 3 |
| -0,12 | -0,1 | -0,11 | 16 | 11,346 | 11 |
| -0,1 | -0,08 | -0,09 | 22 | 23,176 | 23 |
| -0,08 | -0,06 | -0,07 | 25 | 28,423 | 28 |
| -0,06 | -0,04 | -0,05 | 19 | 20,928 | 21 |
| -0,04 | -0,02 | -0,03 | 13 | 9,251 | 9 |
| -0,02 | 0 | -0,01 | 2 | 2,455 | 2 |
| 0 | 0,02 | 0,01 | 0 | 0,391 | 0 |
Визуальный анализ результатов совмещения двух кривых распределения случайной величины x (отклонения от номинального размера диаметра роликов) позволяет заключить, что эмпирическое распределение может рассматриваться как распределение по нормальному закону.
 Вместе с тем, как бы хорошо ни была подобрана теоретическая кривая, между ней и статистическим распределением неизбежны некоторые расхождения. Поэтому возникает вопрос, обусловлены ли эти расхождения только случайными воздействиями и связаны с ограниченным числом наблюдений, или они являются существенными и вызваны тем, что подобранная теоретическая кривая плохо выравнивает исследуемое статистическое распределение. Для ответа на этот вопрос осуществляют проверку гипотезы о законе распределения с помощью критериев согласия.
Вместе с тем, как бы хорошо ни была подобрана теоретическая кривая, между ней и статистическим распределением неизбежны некоторые расхождения. Поэтому возникает вопрос, обусловлены ли эти расхождения только случайными воздействиями и связаны с ограниченным числом наблюдений, или они являются существенными и вызваны тем, что подобранная теоретическая кривая плохо выравнивает исследуемое статистическое распределение. Для ответа на этот вопрос осуществляют проверку гипотезы о законе распределения с помощью критериев согласия.
В заключение приведем последовательность процедур методики выравнивания статистического распределения изучаемой случайной величины X:
- представление в табличной форме исходной статистической совокупности (построение простой статистической совокупности);
- ранжирование значений простой статистической совокупности в порядке их возрастания и построение статистического ряда;
- графическое представление статистического ряда;
- выбор теоретического закона, исходя из физической сущности исследуемого случайной величины и ее эмпирического распределения;
- вычисление статистических характеристик предполагаемого теоретического закона распределения случайной величины;
- графическое представление теоретического распределения и визуальная оценка близости эмпирического распределения к предполагаемому теоретическому закону.
Дата: 2019-02-25, просмотров: 371.
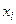
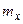

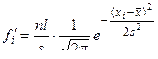
 с округлением
с округлением