Рассмотрим этот метод на примере системы трех линейных уравнений с тремя неизвестными:

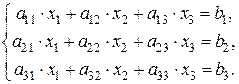
Назовем 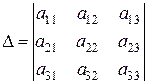 главным определителем системы уравнений.

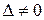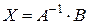Если , то  или ;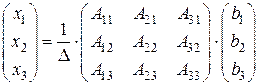

                                                   .

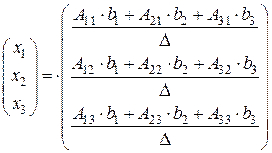Из равенства матриц следует: .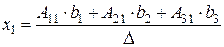

Рассмотрим определитель 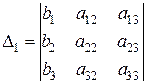, полученный из 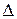путем замены элементов первого столбца на правые части уравнений. Разложим  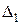по элементам первого столбца: .

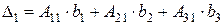Итак, .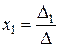

Аналогично можно показать, что

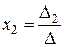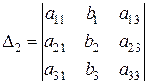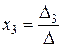, где ; , где .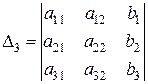

Таким образом, решение данной системы уравнений можно найти по формулам 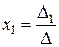; ; 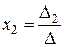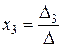, которые называются формулами Крамера.

Полученные формулы можно обобщить для квадратной неоднородной системы с любым числом уравнений 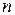. Неизвестное с номером  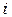можно найти по формуле:

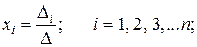
 где 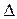 – главный определитель системы;

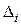 – вспомогательный определитель, полученный из главного заменой коэффициентов при неизвестном  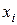на столбец свободных членов.

Анализ полученной формулы и применение ее на практике для решения систем позволяет сделать следующие выводы:

1) если главный определитель системы 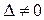, то система имеет единственное решение;

2) если 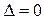, а хотя бы один из вспомогательных определителей 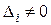, то система не имеет решения;

3) если и главный и все вспомогательные определители равны 0, то система или не имеет решений или имеет бесконечное множество решений.

Пример. Найти решение системы линейных уравнений по формулам Крамера

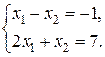
Выпишем и вычислим главный и все вспомогательные определители:

    .

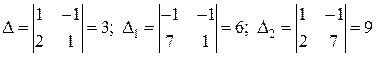По формулам Крамера находим неизвестные:

    .

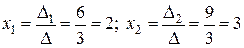Сделаем проверку: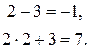

Ответ: .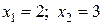

Способ подстановки.

Разберем этот способ на примерах систем из двух линейных уравнений с двумя неизвестными.

Пример 1. Решить систему

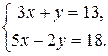
Из первого уравнения выразим 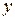 через 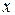, получим 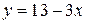. Подставив данное выражение вместо  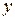во второе уравнение, получим 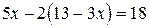. Решением этого линейного уравнения является 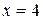. Используем найденное значение для определения 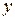: 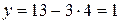. Итак, решением системы будет пара чисел: .

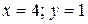Пример 2. Решить систему

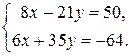
Из второго уравнения выразим 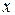 через 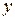: 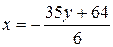. Найденное выражение для  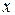подставим в первое уравнение:

    .

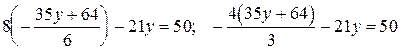Умножим обе части последнего уравнения на 3: 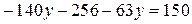, откуда найдем 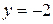, а . Сделав проверку (подставив в оба уравнения системы), убеждаемся, что решением будут .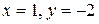

Второй пример показывает, что решение методом подстановки при своей идейной простоте, требует довольно большого количества вычислений и для систем выше второго порядка практически не применяется.

Способ сложения.

Рассмотрим данный способ также на примерах.

Пример 1. Решить систему:

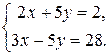
Сложим почленно два уравнения системы, получим 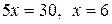. Для определения  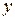подставим найденное значение в любое из уравнений системы, например, в первое: 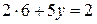, откуда .

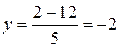Ответ: .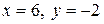

Пример 2. Решить систему:

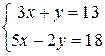
Преобразуем систему, домножив обе части первого уравнения на 2:

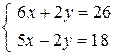
Теперь почленно сложим оба уравнения, получим 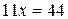, откуда 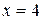. Подставив это значение в первое уравнение, найдем .

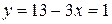Ответ: .