ЛИНЕЙНАЯ АЛГЕБРА
Методическое пособие по выполнению контрольной работы
для дистанционного и заочного обучения студентов
экономических специальностей
Факультет ЗДО
Вологда
2012
УДК: 629. 113. 004. 5
Линейная алгебра: Методическое пособие по выполнению контрольной работы для дистанционного и заочного обучения студентов экономических специальностей. – Вологда: ВоГТУ, 2012. – 44 с.
Утверждено редакционно-издательским советом ВоГТУ
Составители: А.П. Быстроумова, старший преподаватель;
С.В. Иванова, канд. тех. наук, доцент.
Рецензент И.А. Миткевич, канд. эконом. наук, доцент.
Введение
Контрольная работа по линейной алгебре содержит три задания: на графический способ решения задачи линейного программирования; на составление балансового уравнения (модель Леонтьева); на решение прямоугольной системы линейных уравнений при различных способах выбора базиса.
Для выполнения этих заданий необходимы навыки обращения с матрицами и вычисления определителей, умение решать системы линейных уравнений. Поэтому в первой части пособия изложен соответствующий теоретический материал. Во второй части рассмотрены примеры решения задач, в третьей части приведены контрольные задания в 10 вариантах.
I . Элементы линейной алгебры
Простейшие действия с матрицами
1) Транспонирование.
Матрица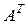 
называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
.
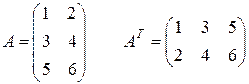2) Сложение (вычитание) матриц.
Матрицы одинаковых размеров можно складывать и вычитать. Чтобы найти сумму или разность двух матриц, нужно сложить или вычесть соответствующие элементы этих матриц.
Пример. Найти сумму и разность матриц А и В, если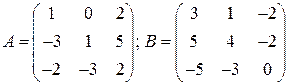 
.
;
.
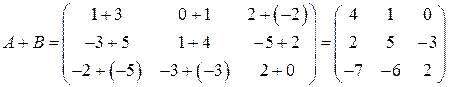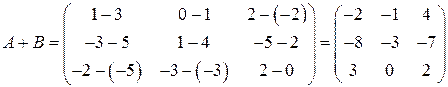Свойства операции сложения матриц:
а)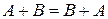 
(перестановочное свойство);
б)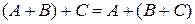 
(сочетательное свойство);
в)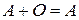 
(если к матрице прибавить нулевую матрицу, то она не изменится).
3) Умножение матрицы на число (скаляр).
Чтобы умножить матрицу на число, нужно все ее элементы умножить на это число, например,
.
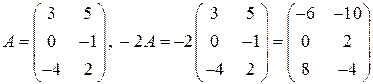Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы.
Свойства операции сложения матриц:
а)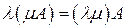 
(сочетательное свойство);
б)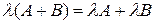 
(распределительное свойство относительно сложения матриц);
в)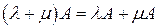 
(распределительное свойство относительно сложения чисел).
Умножение матриц
Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:
.
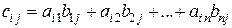Т.е. элемент матрицы С, стоящий в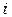 
-той строке и 
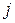-том столбце, равен сумме произведений соответствующих элементов 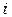-той строки матрицы А и 
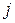-того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Из определения умножения можно также заключить, что умножение матрицы А размера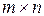 
на матрицу В размера 
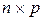дает матрицу С размера 
.
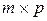Заметим, что квадратные матрицы одного порядка всегда согласованы для умножения.
Пример.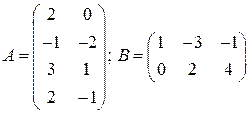 
.
.
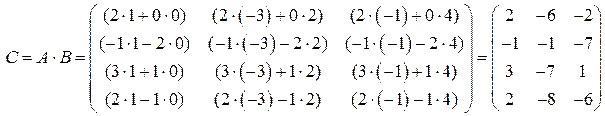Для данных матриц обратное умножение В на А невозможно, т.к. число столбцов в В равно 3, а число строк в матрице А равно 4. Но даже, если возможны оба произведения, они в общем случае могут не совпадать. Проверим:
;
;
.
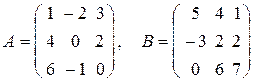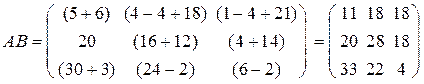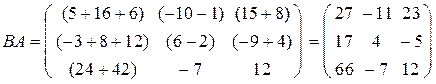Свойства операции умножения матриц:
а)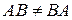 
(в общем случае перестановочное свойство умножения не выполняется, матрицы, для которых оно выполняется, называются перестановочными);
б)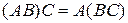 
(сочетательное свойство);
в)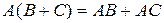 
(распределительное свойство умножения относительно сложения);
г)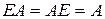 
(умножение на единичную матрицу не меняет матрицы);
д)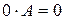 
(умножение на нулевую матрицу дает нулевую матрицу);
Замечание: из того факта, что произведение двух матриц равно 0, не следует обязательно, что или одна из них, или обе вместе равны 0.
Определители и их свойства
Любой квадратной матрице А можно сопоставить число, называемое определителем и обозначаемое |А| или Δ или det A.
Для определителей остаются в силе все понятия введенные для квадратных матриц.
Рассмотрим квадратную матрицу второго порядка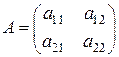 
.
Определителем второго порядка, соответствующим матрице А называется число, которое находится следующим образом:
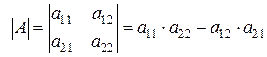, т.е.
определитель второго порядка равен разности произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали.
Пример.
.
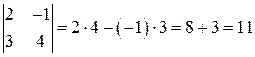Рассмотрим квадратную матрицу третьего порядка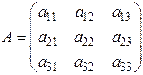 
.
Определителем третьего порядка, соответствующим матрице А называется число, которое находиться следующим образом:
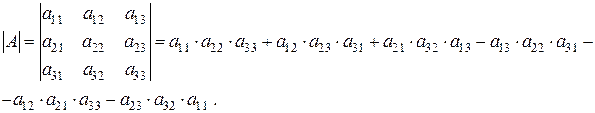Для запоминания формулы вычисления определителей третьего порядка имеется “правило треугольников”:
1. произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали, входят в определитель с тем знаком, который получится при умножении;
2. произведения элементов, стоящих на побочной диагонали и в вершинах треугольников с основаниями, параллельными побочной диагонали, входят в определитель с обратным знаком.
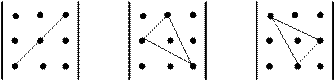
На рисунках элементы определителя обозначены точками.
Пример. Вычислить определитель третьего порядка:
.
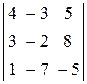Обозначим значение определителя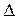 
и найдем его, используя правило треугольников.
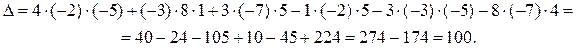
Знание свойств определителей необходимо, чтобы успешно справляться с вычислением определителей любого порядка. Сформулированные без доказательства они легко проверяются непосредственным вычислением.
1) При транспонировании (замене строк на столбцы) величина определителя не меняется.
2) Взаимная перестановка двух строк (или двух столбцов) определителя меняет его знак.
Следствие: определитель с двумя одинаковыми строками или столбцами равен 0.
3) Общий множитель всех элементов строки или столбца можно выносить за знак определителя.
Следствие: определитель с нулевой строкой или столбцом равен 0.
4) При прибавлении к какой-либо строке (или столбцу) другой строки (или столбца), умноженной на произвольное число, величина определителя не изменится.
Используя перечисленные свойства, можно любой ненулевой определитель привести к треугольному виду, тогда он будет равен произведению элементов главной диагонали, т.к. все остальные слагаемые в формуле определителя обратятся в нули.
Пример. Вычислить определитель, приведя его к треугольному виду
.
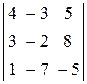Преобразовывать определитель к треугольному виду удобнее, если элемент в первой строке и первом столбце равен 1. Поменяем местами первую и третью строки. (Этого же результата можно было бы добиться, разделив все элементы первой строки на 4 и вынеся 4 за знак определителя.)
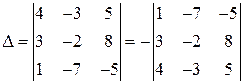
Умножим первую строку на (-3) и прибавим ко второй строке, а затем умножим первую строку на (-4) и прибавим к третьей строке.
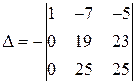
Поменяем местами вторую и третью строки и вынесем общий множитель 25 за знак определителя.
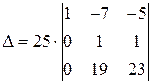
Умножим вторую строку на (-19) и прибавим к третьей.
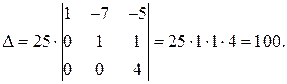
Рассмотрим еще один способ вычисления определителей, а для этого введем два понятия.
Минором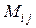 
элемента определителя 
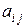называется определитель на единицу меньшего порядка, полученный из исходного вычеркиванием 
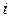-той строки и 
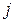-того столбца (т.е. тех, на пересечении которых стоит данный элемент).
Алгебраическим дополнением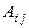 
элемента 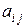называется произведение минора этого элемента на 
:
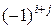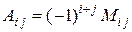
Следует заметить, что у элементов, сумма номеров которых – четное число, алгебраическое дополнение равно минору, а у элементов, сумма номеров которых – нечетное число, алгебраическое дополнение равно минору, взятому с противоположным знаком.
Пример. Найти миноры и алгебраические дополнения всех элементов определителя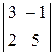 
.
Для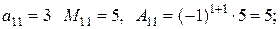 
для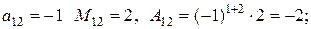 
для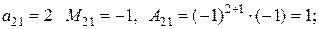 
для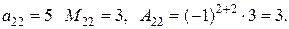 
Преобразуем формулу определителя третьего порядка:
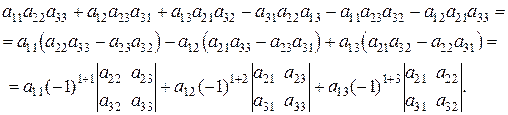
После введенных понятий нетрудно увидеть, что величина определителя равна сумме произведений элементов первой строки на соответствующие алгебраические дополнения:
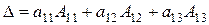
Подобную формулу можно составить, используя для разложения элементы других столбцов или строк, что приводит к общей формуле разложения определителя произвольного порядка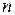 
по элементам произвольной строки или столбца (которая также носит название теоремы Лапласа):
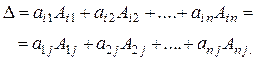
Обратная матрица
Пусть А – квадратная матрица n-го порядка. Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля: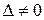 
. В противном случае 
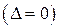матрица А называется вырожденной.
Матрица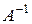 
называется обратной к 
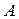, если она удовлетворяет условию:
,
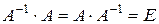где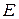 
— единичная матрица.
Докажем, что всякая невырожденная матрица имеет обратную. Проведем доказательство на примере матрицы третьего порядка. Пусть А - невырожденная матрица, с определителем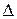 
:
.
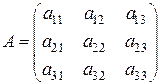Каждый элемент матрицы А заменим его алгебраическим дополнением (оно определяется также, как и алгебраическое дополнение элемента определителя) и составим новую матрицу:
.
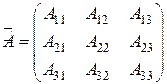Транспонируем последнюю матрицу:
.
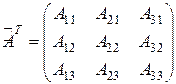Выполним умножение:
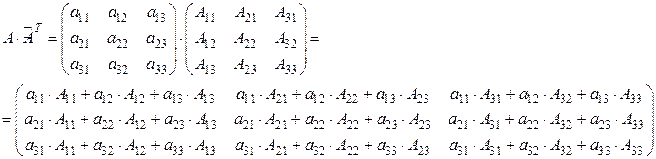
В полученной матрице-произведении каждый элемент главной диагонали равен 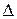, т.к. представляет собой сумму произведений всех элементов соответствующей строки матрицы А на их алгебраические дополнения. Остальные элементы - нули, потому что являются суммами произведений элементов строк матрицы А на алгебраические дополнения соответствующих элементов других строк. Значит,
.
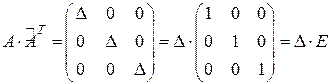Аналогично рассуждая, можно показать, что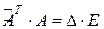 
.
Сравнивая полученные результаты с определением обратной матрицы, получаем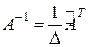 
или 
.
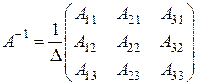Для того чтобы составить обратную матрицу, необходимо:
1) вычислить определитель матрицы;
2) если определитель отличен от 0, то найти алгебраические дополнения всех элементов;
3) поставив алгебраические дополнения на место элементов, составить матрицу и транспонировать ее;
4) разделить элементы транспонированной матрицы из алгебраических дополнений на величину определителя (если элементы матрицы не делятся нацело на определитель, то деление записывают в виде множителя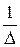 
перед матрицей).
Пример. Найти матрицу, обратную матрице
.
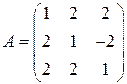1) Вычислим определитель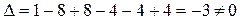 
.
2) Найдем алгебраические дополнения элементов матрицы:
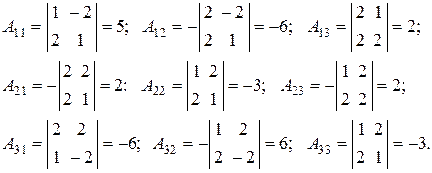
3) Составим матрицу из алгебраических дополнений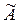 
:
.
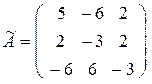и транспонируем ее:
.
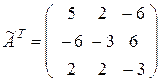3) Выпишем обратную матрицу:
.
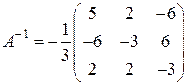Для проверки найдем произведение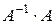 
:
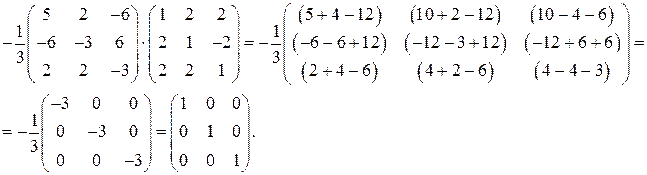
Способ подстановки.
Разберем этот способ на примерах систем из двух линейных уравнений с двумя неизвестными.
Пример 1. Решить систему
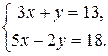
Из первого уравнения выразим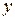 
через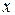 
, получим 
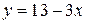. Подставив данное выражение вместо 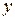во второе уравнение, получим 
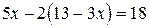. Решением этого линейного уравнения является 
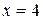. Используем найденное значение для определения : 
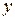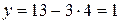. Итак, решением системы будет пара чисел: 
.
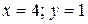Пример 2. Решить систему
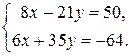
Из второго уравнения выразим 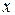через :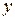 
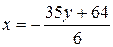. Найденное выражение для 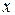подставим в первое уравнение:
.
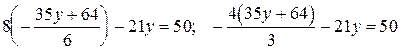Умножим обе части последнего уравнения на 3: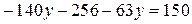 
, откуда найдем 
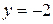, а 
. Сделав проверку (подставив в оба уравнения системы), убеждаемся, что решением будут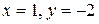 
.
Второй пример показывает, что решение методом подстановки при своей идейной простоте, требует довольно большого количества вычислений и для систем выше второго порядка практически не применяется.
Способ сложения.
Рассмотрим данный способ также на примерах.
Пример 1. Решить систему:
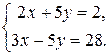
Сложим почленно два уравнения системы, получим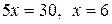 
. Для определения 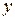подставим найденное значение в любое из уравнений системы, например, в первое: 
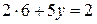, откуда 
.
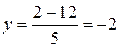Ответ: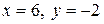 
.
Пример 2. Решить систему:
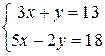
Преобразуем систему, домножив обе части первого уравнения на 2:
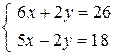
Теперь почленно сложим оба уравнения, получим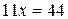 
, откуда 
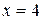. Подставив это значение в первое уравнение, найдем 
.
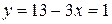Ответ: 
.
Вариант 1
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 2 кг, сырья второго вида 4 кг, третьего – 3 кг. На производство одного изделия В соответственно 6, 2 и 3 кг. Производство обеспечено сырьем первого вида в количестве 486 кг, сырьем второго вида в количестве 396 кг и сырьем третьего вида – 351 кг. Прибыль от реализации одного изделия А составляет 4 тыс. руб., одного изделия В – 6 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 100 | 20 | 10 | 15 | 55 | 70 |
| 2 | 200 | 10 | 40 | 30 | 120 | 150 |
| 3 | 300 | 40 | 50 | 60 | 150 | 200 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции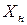 
, учитывая новый товарный план 
.
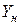Задание 3
Найти решение системы линейных уравнений
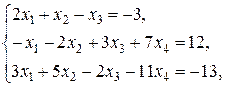
при различных способах выбора базиса.
Вариант 2
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 3 кг, сырья второго вида 4 кг, третьего – 2 кг. На производство одного изделия В соответственно 9, 2 и 2 кг. Производство обеспечено сырьем первого вида в количестве 648 кг, сырьем второго вида в количестве 352 кг и сырьем третьего вида – 208 кг. Прибыль от реализации одного изделия А составляет 4 тыс. руб., одного изделия В – 3 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 200 | 30 | 20 | 30 | 120 | 150 |
| 2 | 100 | 10 | 10 | 15 | 65 | 100 |
| 3 | 300 | 10 | 30 | 60 | 200 | 220 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции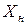 
, учитывая новый товарный план 
.
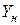Задание 3
Найти решение системы линейных уравнений
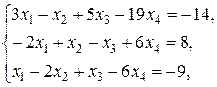
при различных способах выбора базиса.
Вариант 3
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 2 кг, сырья второго вида 6 кг, третьего – 3 кг. На производство одного изделия В соответственно 10, 3 и 5 кг. Производство обеспечено сырьем первого вида в количестве 900 кг, сырьем второго вида в количестве 702 кг и сырьем третьего вида – 540 кг. Прибыль от реализации одного изделия А составляет 2 тыс. руб., одного изделия В – 5 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 200 | 20 | 15 | 10 | 155 | 170 |
| 2 | 300 | 10 | 60 | 30 | 200 | 210 |
| 3 | 100 | 10 | 30 | 15 | 45 | 60 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции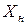 
, учитывая новый товарный план 
.
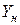Задание 3
Найти решение системы линейных уравнений
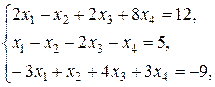
при различных способах выбора базиса.
Вариант 4
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 1 кг, сырья второго вида 4 кг, третьего – 3 кг. На производство одного изделия В соответственно 5, 2 и 5 кг. Производство обеспечено сырьем первого вида в количестве 350 кг, сырьем второго вида в количестве 364 кг и сырьем третьего вида – 420 кг. Прибыль от реализации одного изделия А составляет 6 тыс. руб., одного изделия В – 5 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 200 | 20 | 40 | 20 | 120 | 150 |
| 2 | 400 | 20 | 40 | 10 | 330 | 350 |
| 3 | 200 | 10 | 20 | 20 | 150 | 200 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции 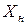, учитывая новый товарный план .
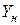Задание 3
Найти решение системы линейных уравнений
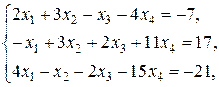
при различных способах выбора базиса.
Вариант 5
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 1 кг, сырья второго вида 4 кг, третьего – 3 кг. На производство одного изделия В соответственно 4, 3 и 4 кг. Производство обеспечено сырьем первого вида в количестве 352 кг, сырьем второго вида в количестве 484 кг и сырьем третьего вида – 440 кг. Прибыль от реализации одного изделия А составляет 5 тыс. руб., одного изделия В – 10 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 200 | 10 | 20 | 40 | 130 | 150 |
| 2 | 200 | 30 | 20 | 40 | 110 | 120 |
| 3 | 400 | 20 | 20 | 80 | 280 | 300 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции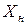 
, учитывая новый товарный план 
.
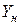Задание 3
Найти решение системы линейных уравнений
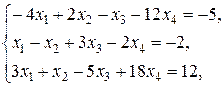
при различных способах выбора базиса.
Вариант 6
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 2 кг, сырья второго вида 3 кг, третьего – 4 кг. На производство одного изделия В соответственно 8, 4 и 3 кг. Производство обеспечено сырьем первого вида в количестве 384 кг, сырьем второго вида в количестве 240 кг и сырьем третьего вида – 264 кг. Прибыль от реализации одного изделия А составляет 8 тыс. руб., одного изделия В – 7 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 300 | 30 | 5 | 60 | 205 | 210 |
| 2 | 100 | 15 | 10 | 20 | 55 | 70 |
| 3 | 400 | 60 | 10 | 80 | 250 | 300 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции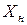 
, учитывая новый товарный план 
.
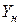Задание 3
Найти решение системы линейных уравнений
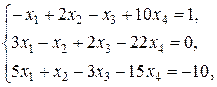
при различных способах выбора базиса.
Вариант 7
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 2 кг, сырья второго вида 4 кг, третьего – 4 кг. На производство одного изделия В соответственно 4, 1 и 3 кг. Производство обеспечено сырьем первого вида в количестве 168 кг, сырьем второго вида в количестве 132 кг и сырьем третьего вида –156 кг. Прибыль от реализации одного изделия А составляет 6 тыс. руб., одного изделия В – 8 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 200 | 20 | 25 | 80 | 75 | 100 |
| 2 | 500 | 20 | 50 | 60 | 370 | 400 |
| 3 | 400 | 30 | 50 | 40 | 280 | 300 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции 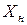, учитывая новый товарный план .
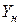Задание 3
Найти решение системы линейных уравнений
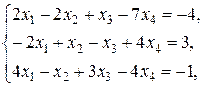
при различных способах выбора базиса.
Вариант 8
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 4 кг, сырья второго вида 1 кг, третьего – 4 кг. На производство одного изделия В соответственно 1, 2 и 3 кг. Производство обеспечено сырьем первого вида в количестве 220 кг, сырьем второго вида в количестве 140 кг и сырьем третьего вида –260 кг. Прибыль от реализации одного изделия А составляет 6 тыс. руб., одного изделия В – 3 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 400 | 60 | 20 | 50 | 270 | 300 |
| 2 | 200 | 20 | 20 | 25 | 135 | 150 |
| 3 | 500 | 40 | 30 | 100 | 330 | 350 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции 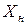, учитывая новый товарный план .
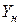Задание 3
Найти решение системы линейных уравнений
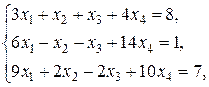
при различных способах выбора базиса.
Вариант 9
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 2 кг, сырья второго вида 7 кг, третьего – 6 кг. На производство одного изделия В соответственно 4, 3 и 1 кг. Производство обеспечено сырьем первого вида в количестве 480 кг, сырьем второго вида в количестве 580 кг и сырьем третьего вида – 450 кг. Прибыль от реализации одного изделия А составляет 6 тыс. руб., одного изделия В – 2 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 200 | 20 | 60 | 10 | 110 | 120 |
| 2 | 400 | 30 | 60 | 10 | 300 | 350 |
| 3 | 100 | 10 | 20 | 5 | 65 | 70 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции 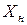, учитывая новый товарный план .
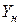Задание 3
Найти решение системы линейных уравнений
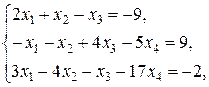
при различных способах выбора базиса.
Вариант 10
Задание 1
Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется затратить сырья первого вида 7 кг, сырья второго вида 1 кг, третьего – 6 кг. На производство одного изделия В соответственно 3, 2 и 1 кг. Производство обеспечено сырьем первого вида в количестве 754 кг, сырьем второго вида в количестве 312 кг и сырьем третьего вида – 585 кг. Прибыль от реализации одного изделия А составляет 3 тыс. руб., одного изделия В – 4 тыс. руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Задачу решить графическим способом.
Задание 2
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Количество валовой | Из нее использовано для про- изводства продукции цехами | Товарная продукция | Новый товарный | ||
| продукции | 1 | 2 | 3 | план | ||
| 1 | 500 | 75 | 40 | 20 | 365 | 370 |
| 2 | 400 | 50 | 20 | 20 | 310 | 320 |
| 3 | 200 | 25 | 40 | 10 | 125 | 150 |
1) Составив технологическую матрицу А, записать в матричном виде простейшую модель производства (балансовое уравнение), сделать проверку составленного уравнения.
2) Вычислив матрицу полных производственных затрат В (точно и приближенно), составить новый план производства продукции 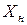, учитывая новый товарный план .
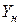Задание 3
Найти решение системы линейных уравнений
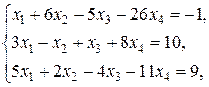
при различных способах выбора базиса.
СОДЕРЖАНИЕ
Введение 3
I . Элементы линейной алгебры
1.Понятие матрицы, различные виды матриц 3
2. Простейшие действия с матрицами 4
3. Умножение матриц 6
4. Определители и их свойства 7
5. Обратная матрица 12
6. Решение систем линейных уравнений 15
II . Примеры решения заданий
1. Графический способ решения задачи линейного программирования 23
2. Составление и решение балансового уравнения 27
3. Решение прямоугольных систем линейных уравнений 30
Контрольная работа 34
СПИСОК ЛИТЕРАТУРЫ
1. Ильин, В. А. Линейная алгебра : учебник для физ. специальностей / В. А. Ильин, Э. Г. Позняк. - Изд. 6-е, стер. . - М. : Физматлит , 2004 . - 278 с.
2. Высшая математика в упражнениях и задачах: учеб. пособие для вузов: в 2 ч. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко . - 7-е изд., испр. - М.: ОНИКС: Мир и Образование, 2009. - 368 с.
3. Карасев, А.И. Математические методы и модели в планировании: учеб. пособие / А.И. Карасев, Н.Ш. Кремер. – М.: Экономика, 1987. – 240 с.
ЛИНЕЙНАЯ АЛГЕБРА
Методическое пособие по выполнению контрольной работы
для дистанционного и заочного обучения студентов
экономических специальностей
Факультет ЗДО
Вологда
2012
УДК: 629. 113. 004. 5
Линейная алгебра: Методическое пособие по выполнению контрольной работы для дистанционного и заочного обучения студентов экономических специальностей. – Вологда: ВоГТУ, 2012. – 44 с.
Утверждено редакционно-издательским советом ВоГТУ
Составители: А.П. Быстроумова, старший преподаватель;
С.В. Иванова, канд. тех. наук, доцент.
Рецензент И.А. Миткевич, канд. эконом. наук, доцент.
Введение
Контрольная работа по линейной алгебре содержит три задания: на графический способ решения задачи линейного программирования; на составление балансового уравнения (модель Леонтьева); на решение прямоугольной системы линейных уравнений при различных способах выбора базиса.
Для выполнения этих заданий необходимы навыки обращения с матрицами и вычисления определителей, умение решать системы линейных уравнений. Поэтому в первой части пособия изложен соответствующий теоретический материал. Во второй части рассмотрены примеры решения задач, в третьей части приведены контрольные задания в 10 вариантах.
Дата: 2019-02-25, просмотров: 222.
