Уравнение называется линейным, если оно содержит неизвестные величины в первой степени и не содержит произведений переменных.
Например, линейными будут следующие уравнения:
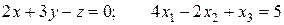 .
.
Для обозначения неизвестных величин в математике обычно используют символы 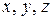 ,
, 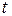 (как в первом примере), а также
(как в первом примере), а также 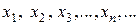 (как во втором примере). В конкретных задачах для неизвестных могут быть использованы другие обозначения.
(как во втором примере). В конкретных задачах для неизвестных могут быть использованы другие обозначения.
Постоянные величины, стоящие при переменных, называют коэффициентами при неизвестных, а постоянные в правой части уравнений – свободными членами уравнений.
Набор из нескольких линейных уравнений для одних и тех же неизвестных называется системой линейных уравнений.
Например:
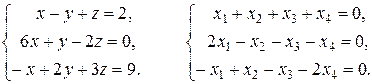
Систему, состоящую из 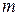 уравнений для
уравнений для 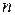 неизвестных, называют системой размера
неизвестных, называют системой размера 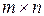 . Если в системе число неизвестных и уравнений совпадает, то она называется квадратной, если не совпадает – прямоугольной. Число уравнений в квадратной системе называется порядком системы.
. Если в системе число неизвестных и уравнений совпадает, то она называется квадратной, если не совпадает – прямоугольной. Число уравнений в квадратной системе называется порядком системы.
Если в системе хотя бы один из свободных членов отличен от нуля, она называется неоднородной, если все свободные члены уравнений равны нулю, она называется однородной.
Решением системы линейных уравнений называется процесс получения тех значений переменных, которые обращают все уравнения системы в тождества. Сам такой набор значений также называется решением системы.
Если система имеет хотя бы одно решение, она называется совместной, если ни одного – то несовместной. Если решение единственно, то система называется определенной, если решений больше одного – то неопределенной.
Рассмотрим различные способы решения систем линейных уравнений.
Матричное решение неоднородной системы линейных уравнений.
Пусть дана система из n линейных уравнений с n неизвестными:
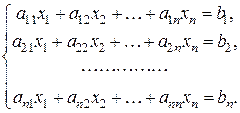
Введем матрицы: 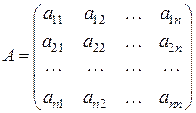 – матрица системы;
– матрица системы;
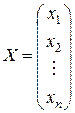 – матрица - столбец из неизвестных;
– матрица - столбец из неизвестных;
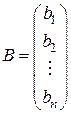 – матрица - столбец из свободных членов.
– матрица - столбец из свободных членов.
Согласно правилу умножения матриц: 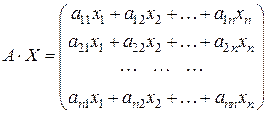 .
.
Используя определение равенства матриц, данную систему уравнений можно записать следующим образом: 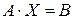 . Это равенство называется матричным уравнением. Здесь в роли неизвестного выступает матрица Х.
. Это равенство называется матричным уравнением. Здесь в роли неизвестного выступает матрица Х.
Пусть определитель матрицы А отличен от нуля 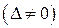 . Значит для нее существует обратная матрица
. Значит для нее существует обратная матрица 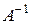 . Умножим обе части матричного уравнения слева на
. Умножим обе части матричного уравнения слева на 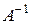 :
: 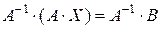
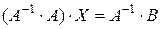
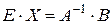
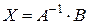 – решение системы уравнений.
– решение системы уравнений.
Пример. Решить систему линейных уравнений с помощью обратной матрицы
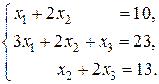
Запишем данную систему матричным уравнением:
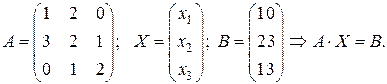
Найдем 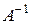 :
:
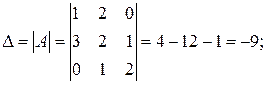
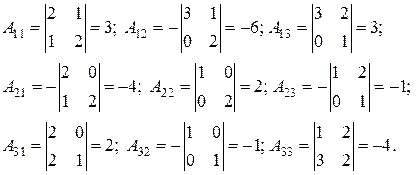

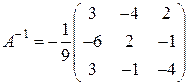 .
.
Найдем Х:
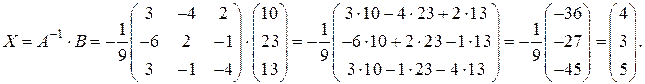
Сделаем проверку: 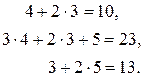
Ответ: 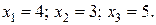
Дата: 2019-02-25, просмотров: 346.