Пример 2. Вычислить определитель 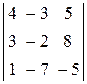 , применяя формулу разложения по элементам второй строки.
, применяя формулу разложения по элементам второй строки.
Вначале найдем миноры и алгебраические дополнения всех элементов второй строки.
Для 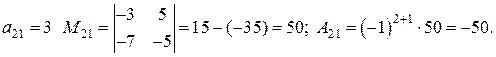
Для 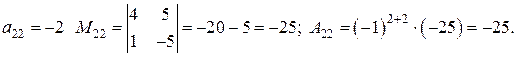
Для 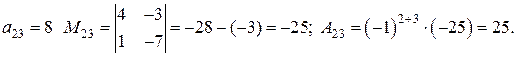
Вычислим определитель по формуле
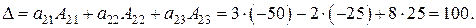
Можно доказать и следующий факт: сумма произведений всех элементов произвольной строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
Например, 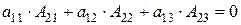 .
.
Замечание: из последнего равенства не следует, что сам определитель равен нулю.
Определители четвертого и более высоких порядков вводятся аналогично. Для них остаются справедливы введенные ранее понятия и свойства. Вычисление таких определителей ведется или с помощью приведения их к треугольному виду или разложением по элементам строк (столбцов).
Обратная матрица
Пусть А – квадратная матрица n-го порядка. Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля: 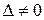 . В противном случае
. В противном случае 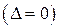 матрица А называется вырожденной.
матрица А называется вырожденной.
Матрица 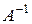 называется обратной к
называется обратной к 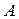 , если она удовлетворяет условию:
, если она удовлетворяет условию:
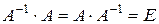 ,
,
где 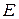 — единичная матрица.
— единичная матрица.
Докажем, что всякая невырожденная матрица имеет обратную. Проведем доказательство на примере матрицы третьего порядка. Пусть А - невырожденная матрица, с определителем 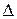 :
:
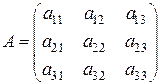 .
.
Каждый элемент матрицы А заменим его алгебраическим дополнением (оно определяется также, как и алгебраическое дополнение элемента определителя) и составим новую матрицу:
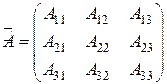 .
.
Транспонируем последнюю матрицу:
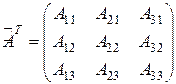 .
.
Выполним умножение:
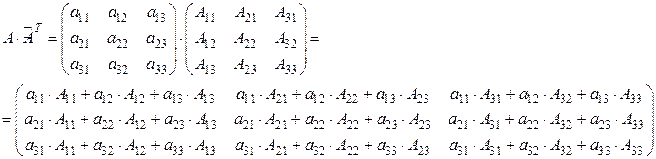
В полученной матрице-произведении каждый элемент главной диагонали равен 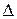 , т.к. представляет собой сумму произведений всех элементов соответствующей строки матрицы А на их алгебраические дополнения. Остальные элементы - нули, потому что являются суммами произведений элементов строк матрицы А на алгебраические дополнения соответствующих элементов других строк. Значит,
, т.к. представляет собой сумму произведений всех элементов соответствующей строки матрицы А на их алгебраические дополнения. Остальные элементы - нули, потому что являются суммами произведений элементов строк матрицы А на алгебраические дополнения соответствующих элементов других строк. Значит,
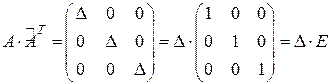 .
.
Аналогично рассуждая, можно показать, что 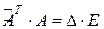 .
.
Сравнивая полученные результаты с определением обратной матрицы, получаем 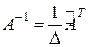 или
или 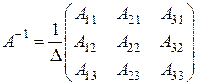 .
.
Для того чтобы составить обратную матрицу, необходимо:
1) вычислить определитель матрицы;
2) если определитель отличен от 0, то найти алгебраические дополнения всех элементов;
3) поставив алгебраические дополнения на место элементов, составить матрицу и транспонировать ее;
4) разделить элементы транспонированной матрицы из алгебраических дополнений на величину определителя (если элементы матрицы не делятся нацело на определитель, то деление записывают в виде множителя 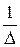 перед матрицей).
перед матрицей).
Пример. Найти матрицу, обратную матрице
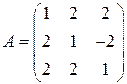 .
.
1) Вычислим определитель 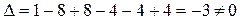 .
.
2) Найдем алгебраические дополнения элементов матрицы:
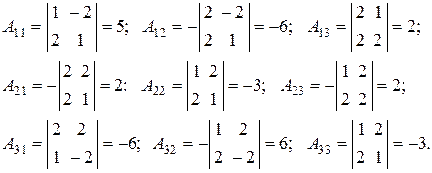
3) Составим матрицу из алгебраических дополнений 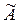 :
:
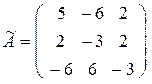 .
.
и транспонируем ее:
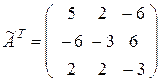 .
.
3) Выпишем обратную матрицу:
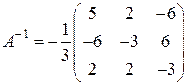 .
.
Для проверки найдем произведение 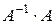 :
:
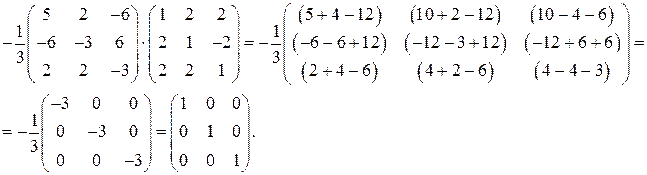
Дата: 2019-02-25, просмотров: 350.