1) Транспонирование.
Матрица 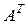 называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
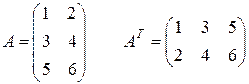 .
.
2) Сложение (вычитание) матриц.
Матрицы одинаковых размеров можно складывать и вычитать. Чтобы найти сумму или разность двух матриц, нужно сложить или вычесть соответствующие элементы этих матриц.
Пример. Найти сумму и разность матриц А и В, если 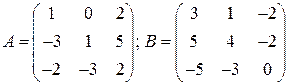 .
.
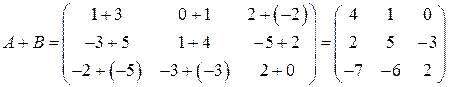 ;
;
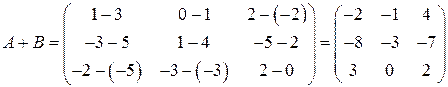 .
.
Свойства операции сложения матриц:
а) 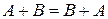 (перестановочное свойство);
(перестановочное свойство);
б) 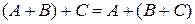 (сочетательное свойство);
(сочетательное свойство);
в) 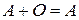 (если к матрице прибавить нулевую матрицу, то она не изменится).
(если к матрице прибавить нулевую матрицу, то она не изменится).
3) Умножение матрицы на число (скаляр).
Чтобы умножить матрицу на число, нужно все ее элементы умножить на это число, например,
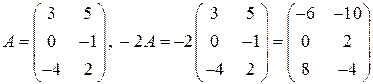 .
.
Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы.
Свойства операции сложения матриц:
а) 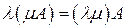 (сочетательное свойство);
(сочетательное свойство);
б) 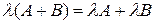 (распределительное свойство относительно сложения матриц);
(распределительное свойство относительно сложения матриц);
в) 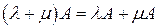 (распределительное свойство относительно сложения чисел).
(распределительное свойство относительно сложения чисел).
Умножение матриц
Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:
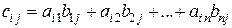 .
.
Т.е. элемент матрицы С, стоящий в 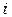 -той строке и
-той строке и 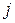 -том столбце, равен сумме произведений соответствующих элементов
-том столбце, равен сумме произведений соответствующих элементов 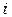 -той строки матрицы А и
-той строки матрицы А и 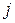 -того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
-того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Из определения умножения можно также заключить, что умножение матрицы А размера 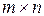 на матрицу В размера
на матрицу В размера 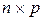 дает матрицу С размера
дает матрицу С размера 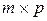 .
.
Заметим, что квадратные матрицы одного порядка всегда согласованы для умножения.
Пример. 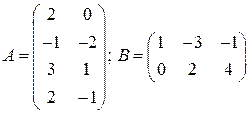 .
.
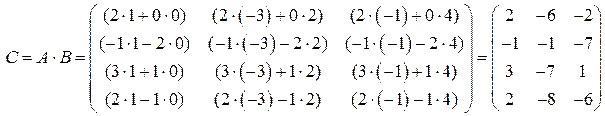 .
.
Для данных матриц обратное умножение В на А невозможно, т.к. число столбцов в В равно 3, а число строк в матрице А равно 4. Но даже, если возможны оба произведения, они в общем случае могут не совпадать. Проверим:
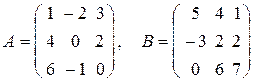 ;
;
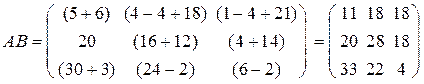 ;
;
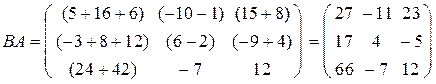 .
.
Свойства операции умножения матриц:
а) 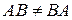 (в общем случае перестановочное свойство умножения не выполняется, матрицы, для которых оно выполняется, называются перестановочными);
(в общем случае перестановочное свойство умножения не выполняется, матрицы, для которых оно выполняется, называются перестановочными);
б) 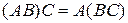 (сочетательное свойство);
(сочетательное свойство);
в) 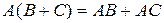 (распределительное свойство умножения относительно сложения);
(распределительное свойство умножения относительно сложения);
г) 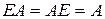 (умножение на единичную матрицу не меняет матрицы);
(умножение на единичную матрицу не меняет матрицы);
д) 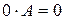 (умножение на нулевую матрицу дает нулевую матрицу);
(умножение на нулевую матрицу дает нулевую матрицу);
Замечание: из того факта, что произведение двух матриц равно 0, не следует обязательно, что или одна из них, или обе вместе равны 0.
Определители и их свойства
Любой квадратной матрице А можно сопоставить число, называемое определителем и обозначаемое |А| или Δ или det A.
Для определителей остаются в силе все понятия введенные для квадратных матриц.
Рассмотрим квадратную матрицу второго порядка 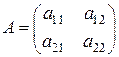 .
.
Определителем второго порядка, соответствующим матрице А называется число, которое находится следующим образом:
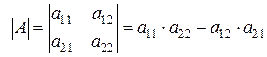 , т.е.
, т.е.
определитель второго порядка равен разности произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали.
Пример.
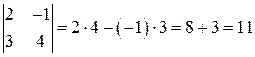 .
.
Рассмотрим квадратную матрицу третьего порядка 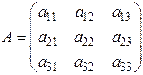 .
.
Определителем третьего порядка, соответствующим матрице А называется число, которое находиться следующим образом:
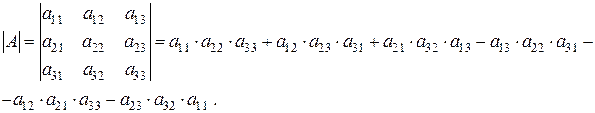 Для запоминания формулы вычисления определителей третьего порядка имеется “правило треугольников”:
Для запоминания формулы вычисления определителей третьего порядка имеется “правило треугольников”:
1. произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали, входят в определитель с тем знаком, который получится при умножении;

2. произведения элементов, стоящих на побочной диагонали и в вершинах треугольников с основаниями, параллельными побочной диагонали, входят в определитель с обратным знаком.
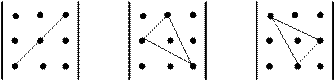
На рисунках элементы определителя обозначены точками.
Пример. Вычислить определитель третьего порядка:
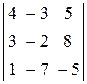 .
.
Обозначим значение определителя 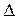 и найдем его, используя правило треугольников.
и найдем его, используя правило треугольников.
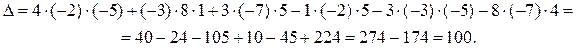
Знание свойств определителей необходимо, чтобы успешно справляться с вычислением определителей любого порядка. Сформулированные без доказательства они легко проверяются непосредственным вычислением.
1) При транспонировании (замене строк на столбцы) величина определителя не меняется.
2) Взаимная перестановка двух строк (или двух столбцов) определителя меняет его знак.
Следствие: определитель с двумя одинаковыми строками или столбцами равен 0.
3) Общий множитель всех элементов строки или столбца можно выносить за знак определителя.
Следствие: определитель с нулевой строкой или столбцом равен 0.
4) При прибавлении к какой-либо строке (или столбцу) другой строки (или столбца), умноженной на произвольное число, величина определителя не изменится.
Используя перечисленные свойства, можно любой ненулевой определитель привести к треугольному виду, тогда он будет равен произведению элементов главной диагонали, т.к. все остальные слагаемые в формуле определителя обратятся в нули.
Пример. Вычислить определитель, приведя его к треугольному виду
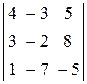 .
.
Преобразовывать определитель к треугольному виду удобнее, если элемент в первой строке и первом столбце равен 1. Поменяем местами первую и третью строки. (Этого же результата можно было бы добиться, разделив все элементы первой строки на 4 и вынеся 4 за знак определителя.)
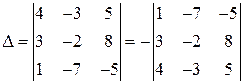
Умножим первую строку на (-3) и прибавим ко второй строке, а затем умножим первую строку на (-4) и прибавим к третьей строке.
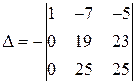
Поменяем местами вторую и третью строки и вынесем общий множитель 25 за знак определителя.
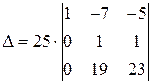
Умножим вторую строку на (-19) и прибавим к третьей.
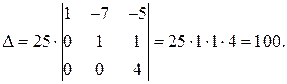
Рассмотрим еще один способ вычисления определителей, а для этого введем два понятия.
Минором 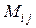 элемента определителя
элемента определителя 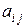 называется определитель на единицу меньшего порядка, полученный из исходного вычеркиванием
называется определитель на единицу меньшего порядка, полученный из исходного вычеркиванием 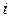 -той строки и
-той строки и 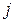 -того столбца (т.е. тех, на пересечении которых стоит данный элемент).
-того столбца (т.е. тех, на пересечении которых стоит данный элемент).
Алгебраическим дополнением 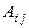 элемента
элемента 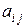 называется произведение минора этого элемента на
называется произведение минора этого элемента на 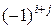 :
:
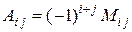
Следует заметить, что у элементов, сумма номеров которых – четное число, алгебраическое дополнение равно минору, а у элементов, сумма номеров которых – нечетное число, алгебраическое дополнение равно минору, взятому с противоположным знаком.
Пример. Найти миноры и алгебраические дополнения всех элементов определителя 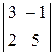 .
.
Для 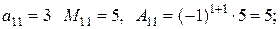
для 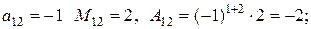
для 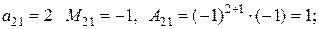
для 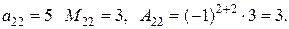
Преобразуем формулу определителя третьего порядка:
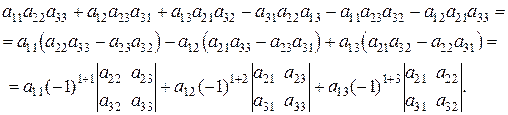
После введенных понятий нетрудно увидеть, что величина определителя равна сумме произведений элементов первой строки на соответствующие алгебраические дополнения:
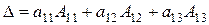
Подобную формулу можно составить, используя для разложения элементы других столбцов или строк, что приводит к общей формуле разложения определителя произвольного порядка 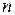 по элементам произвольной строки или столбца (которая также носит название теоремы Лапласа):
по элементам произвольной строки или столбца (которая также носит название теоремы Лапласа):
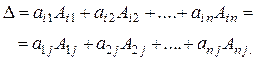
Дата: 2019-02-25, просмотров: 372.