Известно, что показатели безотказности Х1, долговечности Х2 и ремонтопригодности Х3 инструмента являются случайными величинами, числовые характеристики и законы распределений которых определяются по результатам экспериментальных исследований. Вследствие этого критерий оптимизации КИ также является случайной величиной. Представление критерия оптимизации КИ как функции случайных аргументов позволяет вычислять его числовые характеристики - математическое ожидание и дисперсию с учетом характеристик случайных аргументов.
Пусть имеется система случайных аргументов с заданными числовыми характеристиками системы: математическими ожиданиями mx и дисперсиями Dx,:
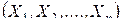. (15.6)
; 
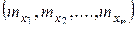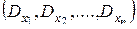. (15.7)
Случайная величина Y есть нелинейная функция случайных аргументов X 1 , X 2 ,…, Xn:
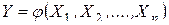. (15.8)
Разлагая функцию y=j(x 1 , x 2 ,…, xn) в ряд Тейлора в окрестности точки (mx 1 , mx 2 ,…, mxn) и сохраняя в разложении члены не выше второго порядка, имеем:
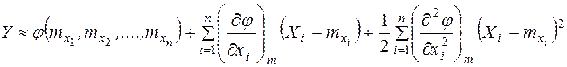. (15.9)
Математическое ожидание my величины Y определяется следующим образом:
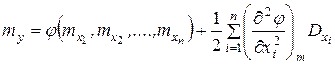. (15.10)
Математические ожидания mxi и дисперсии Dxi относительных показателей безотказности, долговечности и ремонтопригодности инструмента равны соответственно:
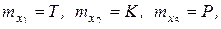(15.11)
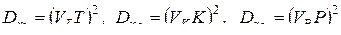, (15.12)
где VT, VK, VP – коэффициенты вариации относительных показателей безотказности, долговечности и ремонтопригодности, характеризующие рассеивание указанных показателей надежности.
Математическое ожидание критерия оптимизации определяется следующим образом:
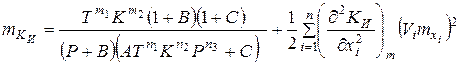. (15.13)
Полученная зависимость свидетельствует о том, что математическое ожидание критерия оптимизации как функции случайных аргументов m КИ отличается от его значения, рассчитанного общепринятым методом по математическим ожиданиям этих аргументов j(mxi). Количественно это отличие характеризуется значением второго слагаемого в формуле (11), которое с достаточной степенью точности может служить оценкой погрешности приближенной аппроксимации случайных моделей детерминированными. Полученная зависимость устанавливает взаимосвязь математического ожидания критерия оптимизации m КИ как функции случайных аргументов с рассеиванием показателей надежности инструмента.
Для поиска оптимальных значений параметров оптимизации - показателей безотказности Т opt, долговечности К opt и ремонтопригодности Р opt с учетом случайного характера критерия оптимизации и самих параметров оптимизации численными методами решается система дифференциальных уравнений:
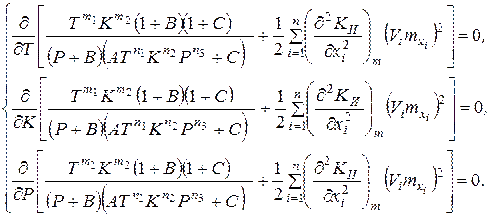(15.14)
Представление критерия оптимизации как функции случайного аргумента дает возможность количественно оценить влияние рассеивания показателей надежности, характеризуемых коэффициентами вариации V, на их оптимальный уровень.
На рис. 15.2 представлены графики зависимости оптимального уровня показателей безотказности Т opt, долговечности К opt и ремонтопригодности Р opt от коэффициентов их вариации V при однопараметрической оптимизации для условий: С = 5; В = 50; А =0,5; n 1 = n 2 = 1,5; n 3 =-1,5; m 1 = 0,2; m 2 = 0,4.
С увеличением коэффициента вариации оптимальные уровни показателей безотказности Т opt и долговечности К opt снижаются, а ремонтопригодности Р opt - увеличивается. При значении коэффициента вариации V = 0 рассеивание отсутствует, что соответствует детерминированной модели, для которой оптимальные уровни показателей безотказности Т opt, долговечности К opt и ремонтопригодности Р opt рассчитываются в соответствии с формулами (15.4). При коэффициенте вариации V<0,4 степень его влияния на оптимальные уровни показателей безотказности Т opt, долговечности К opt и ремонтопригодности Р opt весьма незначительна, что также свидетельствует о возможности использования детерминированной модели и расчетных формул (15.4) с погрешностью, не превышающей 10%.
Для приближенной оценки оптимальных уровней показателей безотказности Т opt, долговечности К opt и ремонтопригодности Р opt при однопараметрической оптимизации в расчетные формулы должны вводиться поправочные коэффициенты μТ, μК, μР, определяемые с использованием представленных на рис. 15.3 графиков их зависимости от коэффициента вариации V:
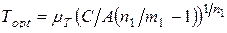, (15.15)
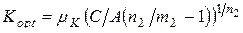, (15.16)
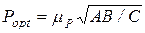. (15.17)
Однопараметрическая оптимизация целесообразна тогда, когда изменяется только один из показателей надежности при постоянных или незначительно изменяющихся остальных. В том случае, когда одновременно изменяются все показатели надежности, что наиболее характерно для режущего инструмента, необходима трехпараметрическая оптимизация показателей безотказности, долговечности и ремонтопригодности. Оптимальные уровни показателей надежности при многопараметрической оптимизации могут быть получены численными методами.
В качестве примера для одних и тех же ранее указанных условий приведены результаты одновременной оптимизации уровня качества по трем параметрам в сравнении с однопараметрической оптимизацией при коэффициенте вариации V<0,4. Результаты представляются в виде вектора оптимальных значений Xopt(Т opt, К opt, Р opt): при трехпараметрической оптимизации - Xopt(1,6; 1,5; 1,7); при однопараметрической оптимизации - Xopt(1,3; 1,0; 1,0); Xopt(1,0; 2,0; 1,0); Xopt(1,0; 1,0; 1,3);
Таким образом, на основании анализа критерия оптимизации - интегрального показателя качества режущего инструмента как функции случайного аргумента, получены аналитические зависимости, позволяющие количественно учитывать рассеивание показателей безотказности, долговечности и ремонтопригодности режущего инструмента при определении их оптимального уровня.
Лекция 16. Стохастическая оптимизация режимов резания
На основании разработанных зависимостей показателей безотказности и долговечности от условий эксплуатации могут быть рассчитаны поправочные коэффициенты на режимы резания – скорость резания, подачу и глубину, обеспечивающие заданный гарантированный уровень надежности с учетом вероятности возникновения неблагоприятных видов отказов, связанных с разрушением режущего инструмента.
Критерий оптимальности в зависимости от режимов резания может быть представлен следующим образом:
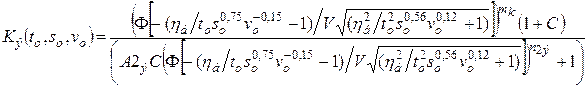.(16.1)
Полученная зависимость позволяет количественно оценивать влияние режимов обработки на установленный критерий оптимальности.
На рис. 16.1 в виде поверхностей показаны графики двухпараметрических зависимостей, характеризующих одновременное влияние режимов резания на критерий оптимальности K э ( to , so ,), K э ( so , Vo ).
Представленные графики свидетельствуют об экстремальном характере рассмотренного критерия и о наличии оптимальных значений относительных режимов резания, которые могут быть рассчитаны численными методами.
Задача одновременной многопараметрической оптимизации режимов резания решается численными методами. Для расчета оптимальных значений параметров оптимизации определяются и приравниваются к нулю частные производные целевой функции по каждому отдельному параметру, составляется и решается система полученных уравнений.
Поиск корней указанной системы выполняется с использованием пакета прикладных программ Mathcad.
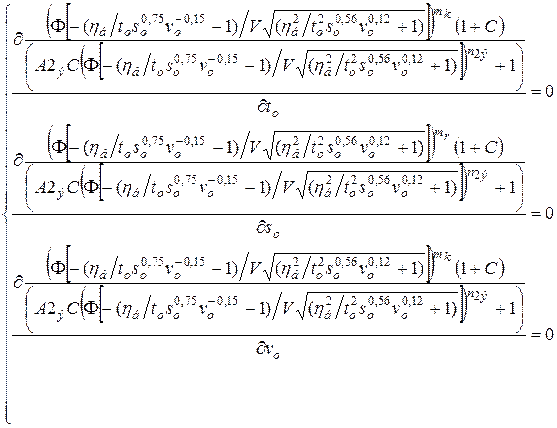. (16.2)
На основании разработанных зависимостей показателей безотказности и долговечности от условий эксплуатации могут быть рассчитаны поправочные коэффициенты на режимы резания – скорость резания, подачу и глубину, обеспечивающие оптимальный уровень надежности с учетом вероятности возникновения неблагоприятных видов отказов, связанных с разрушением режущего инструмента.
ВОПРСЫ ДЛЯ САМОПРОВЕРКИ
1. Каков критерий оптимальности и параметры оптимизации уровня качества инструмента?
2. В чем заключается случайный характер критерия оптимальности и параметров качества инструмента?
3. Как строится математическая модель оптимизации уровня качества инструмента?
4. В чем заключается особенность стохастической оптимизации режимов резания?
5. Каков критерий оптимальности при стохастической оптимизации режимов резания?
6. В каких случаях необходимо учитывать случайный характер критерия оптимальности и параметров оптимизации?
7. В чем отличие метода Лагранжа и метода стохастической оптимизации?
Список литературы
1. Грановский Г.И., Грановский В.Г. Резание металлов: Учебник для машиностр. и приборостр. спец. вузов. - М.: Высш. шк., 1985. - 304с.
2. Старков В.К. Обработка резанием. Управление стабильностью и качеством в автоматизированном производстве. - М.: Машиностроение. 1989. - 296с.
3. Ящерицын П.И.. Еременко М.Л., Фельдштейн Е.Э. Теория резания. Физические и тепловые процессы в технологических системах: Учеб. для вузов. - Мн.: Выш. шк., 1990. - 512с.
4. Справочник технолога-машиностроителя. В 2-х т. Т. 2 / Под ред. А.Г. Косиловой, Р.К. Мещерякова. - М.: Машиностроение . 1985. - 496с.
5. Справочник по обработке металлов резанием / Ф.Н. Абрамов, В.В. Коваленко, В.Е. Любимов и др. - К.: Технiка, 1983. - 239с.
6. Обработка металлов резанием: Справочник технолога / А.А. Панов, В.В. Аникин, Н.Г. Бойм и др.; Под общ. ред. А.А. Панова. - М.: Машиностроение,1988. -736с.
7. Теория резания металлов в примерах и задачах / О.С. Кроль, Е.У. Зарубицкий, В.Н. Кисилев. - К.: УМК ВО, 1992. -124 с.
8. Оптимизация и управление процессом резания: Учеб. пособие / О.С. Кроль, Г.Л. Хмеловский. – К.: УМК ВО, 1991. – 140с.
8. Методические указания и контрольные задания по курсу “Основы управления процессом резания” (для студентов специальности 7.090202) / Т.Г. Ивченко. - Донецк: ДНТУ, 2005. - 30 с.
СОДЕРЖАНИЕ
| Введение | 4 |
| Современные требования к управлению процессом резания Лекция 1. Оптимизация как метод управления | 5 |
| Лекция 2. Однопараметрическая оптимизация режимов резания | 7 |
| Лекция 3. Формирование системы ограничений при механообработке | 10 |
| Метод линейного программирования Лекция 4. Расчет оптимальных режимов резания при черновой обработке | 13 |
| Лекция 5. Расчет оптимальных режимов резания при получистовой обработке | 18 |
| Лекци я 6 .Расчет оптимальных режимов резания при чистовой обработке | 22 |
| Лекция 7 . Расчет оптимальных режимов резания при тонком точении | 26 |
| Лекция 8. Расчет оптимальных режимов резания при точении труднообрабатываемых материалов | 29 |
| Метод геометричесого программирования Лекция 9. Общие сведения о методе геометрического программирования | 35 |
| Лекция 10. Расчет оптимальных режимов резания при черновой обработке МГП | 39 |
| Лекция 11. Расчет оптимальных режимов резания при чистовой обработке МГП | 42 |
| Метод неопределенных множителей лагранжа Лекция 12. Общие сведения о методе Лагранжа | 44 |
| Лекция 13. Примеры расчета оптимальных режимов резания методом Лагранжа | 47 |
| Лекция 14. Расчет оптимальных режимов резания при двухпроходной обработке методом Лагранжа | 49 |
| Стохастическая оптимизация уровня качества режущего инструмента и режимов резания Лекция 15. Представления о качестве инструмента как системы случайных величин | 54 |
| Лекция 16. Стохастическая оптимизация режимов резания | 60 |
| Список литературы | 62 |
КОНСПЕКТ ЛЕКЦИЙ
по курсу «Основы управления процессом резания»
(для студентов направления подготовки 6.050503 «Машиностроение»
специализации «Технология машиностроения» всех форм обучения)
Составитель Т.Г. Ивченко, доц.
Дата: 2019-02-25, просмотров: 193.
