Метод геометрического программирования возник в связи с попыткой учесть особенности инженерных постановок для поиска оптимальных проектных решений. Необходимо, в первую очередь, отметить основное требование МГП, которое состоит в том, что все компоненты задачи оптимизации должны быть выражены количественно в виде обобщенных положительных полиномов называемых позиномами, от управляемых параметров. Во многих технических приложениях целевая функция и ограничения представлены в виде суммы компонентов, каждый из которых может быть выражен в виде степенной функции

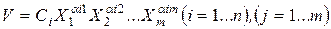                        (9.1)

где С _i- положительная константа; α _ij- произвольные вещественные числа; X_l- оптимизируемые параметры.

В противоположность классическим косвенным методам (множителей Лагранжа и др.) в МГП вначале находят экстремум целевой функции и относительный вклад каждой компоненты в его значение, а затем - оптимальные значения переменных параметров. При исследовании задачи минимизации позиномов (8.1) используется известное неравенство:

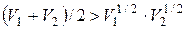,                                 (9.2)

где V ₁ , V ₂ - неотрицательные числа.

При рассмотрении геометрического неравенства с n неотрицательными числами, когда некоторые из них равны между собой, вводится понятие взвешенных средних. В такой обобщенной форме геометрическое неравенство может быть использовано для нахождения оценок снизу для позиномов. В наиболее простой постановке задачи ГП не рассматриваются вынужденные (активные) ограничения (к неактивным ограничениям относятся требования к знаку констант С i - позинома и к знаку оптимизируемых переменных Xj). В общем случае для произвольных положительных чисел и таких положительных весов, для которых 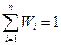, имеет место соотношение  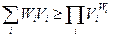последнее выражение можно записать как

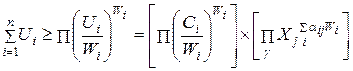                  (9.3).

В неравенстве (8.3) левая часть получила название прямой функции g ( x ) правая - преддвойственной функции V ( W ,х). Показатели степени при X_j , являются линейными комбинациями 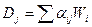. Если выбрать веса W_i так, чтобы все D_j обратились в нуль, то преддвойственная функция не будет зависеть от переменных X_j и примет вид  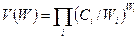тогда неравенство (8.3) сводится к системе соотношений:

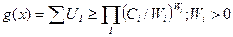                                   (9.4)

                                                         (9.5)

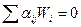                                                      (9.6)

Система соотношений (8.4)-(8.5) получила название двойственной постановки МГП, согласно которой задача сводится к максимизации двойственной функции V ( W ), при линейных ограничениях на двойственные переменные, называемые условиями нормализации (8.5) и условиями ортогональности (8.6). Поскольку из неравенства (8.3) следует, что g (х) имеет положительную нижнюю грань (оценка снизу для позиномов), то можно записать.

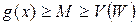                                        (9.7)

Из (9.7) видно, что M является оценкой сверху двойственной функции для любого выбора весов W, при котором показатели d_j обращаются в нуль. Следует заметить, что поскольку равенство (8.3) достигается при 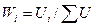 существует простая связь между прямыми X и двойственными W переменными. Действительно, оптимальные значения прямых переменных и двойственных, удовлетворяют следующему соотношению:

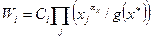                                          (9.8)

На основе сказанного целесообразно сделать постановку задачи оптимизации по МГП в такой последовательности.

Прямая задача МГП:

минимизировать 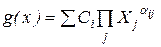при ограничениях Х _j>0, C_i>0

Двойственная задача МГП:

максимизировать 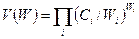при ограничениях ,

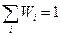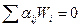
B большинстве реальных задач на искомые переменные X_j накладываются активные (вынужденные) ограничения, не вытекающие из приведенной ранее постановки.

Постановка прямой задачи ГП с ограничениями представлена далее:

Минимизировать

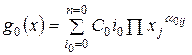;                                                 (9.9)

при ограничениях Х>0; k =1, 2, 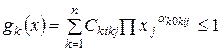.          (9.10)