Формирование целевой функции.

В качестве критерия оптимизации принимается переменная часть себестоимости обработки детали режущим инструментом за один проход, зависящая от режимов резания:

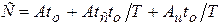,                                             (9.11)

где А - себестоимость станко - минуты, А_и – стоимость одного периода стойкости инструмента; t_o- основное время обработки; t_c - время смены инструмента; T - стойкость инструмента.

Для решения данной задачи (с учетом соотношения n =1000 V /π D) используем аналитическое выражение

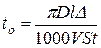.                                               (9.12)

где D, L - диаметр и длина обрабатываемой поверхности; Δ припуск на обработку; V - скорость резания; S – подача; t – глубина резания;

Стойкостное уравнение представим в следующем виде:

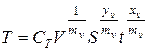.                                             (9.13)

где C_Т – коэффициент и  x, y, m – показатели, характеризующие степень влияния глубины t, подачи S и стойкости T на скорость резания V, определяемые в зависимости от условий обработки.

Целевая функция, выражающая зависимость переменной части себестоимости от режимов резания, с учетом известных соотношений основного времени обработки и стойкости инструмента с режимами, имеет вид:

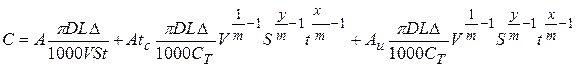, (9.14)

При заданной глубине резания в условиях однопроходной обработки (t = Δ).

Тогда целевая функция может быть представлена следующим образом:

,                                          (9.15)

где ; ; ; .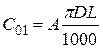

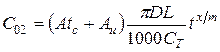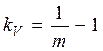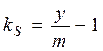 Формирование системы технических ограничений.

Ограничения, которые требуется учесть при решении конкретных задач, необходимо представить в следующем виде:

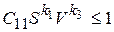,                                                     (9.16)

где С₁₁ – коэффициент, k₁ , k₂ – показатели, характеризующие степень влияния подачи S и скорости V на исследуемое ограничение.

Математическая модель задачи оптимизации скорости резания и подачи представляется следующим образом:

1) прямая задача МГП - минимизировать

                                  (9.17)

при ограничениях V > 0, S  > 0, С₀₁ > 0, С₀₂  > 0;

2) двойственная задача МГП - максимизировать

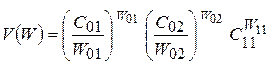                                          (9.18)

при ограничениях

                                        (9.19)

Согласно МГП на первом этапе оптимизации скорости резания и подачи решается система линейных уравнений (8.19) для нахождения W ₀₁, W ₀₂, W ₁₁ и т.д_.

Особенность МГП является возможность уже на первом этапе решения оценить вклад каждой составляющей целевой функции в общую себестоимость С - (8.11). Стоимость первой составляющей, связанной с машинной обработкой оценивается весомостью W ₀₁, а составляющей, связанной со сменой инструмента - W ₀₂.

Далее вычисляется экстремум целевой функции, для чего рассчитывается максимум двойственной функции V( W ) - (8.18). На основании найденного экстремума целевой функции составляется система линейных уравнений для определения оптимальных режимов резания:

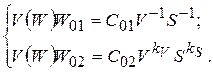                                         (9.20)

В результате решения этой системы определяются оптимальные подача S_о и скорость резания V_о.

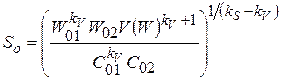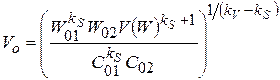; . (9.21)

Лекция 10. Расчет оптимальных режимов резания при черновой обработке

1. Разработка математической модели оптимизации черновой обработки

2. Расчет оптимальных режимов резания при черновом точении и растачивании

3. Обоснование достижения минимума целевой функциии - себестоимости