На черновых операциях припуск на обработку часто снимают за несколько проходов. При двухпроходной обработке себестоимость технологического перехода по обточке цилиндрической поверхности определяется из уравнения.

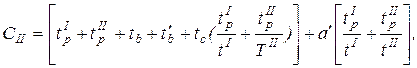
где 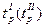– время резания при первом (втором) проходе;

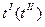 - стойкость инструмента при первом (втором) проходе; t_в- вспомогательное время на переход; - время перемещения и установки инструмента для выполнения второго прохода t_c – время смены инструмента.

Стойкость инструмента задается уравнениями

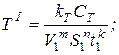
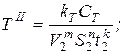
где V ₁ , S ₁ , t ₁ ( V ₂ , S ₂ , t ₂ )– режимы резания соответственно на первом и втором проходе.

    Очевидно, что минимизация себестоимости двухпроходной обработки сводится к оптимальному распределению общего припуска между проходами и к независимому поиску оптимальных значений скорости резания и подачи на каждом проходе при фиксированной глубине резания.

    Рассмотрим ситуацию, когда на первом и на втором проходе были активны силовые ограничения. Тогда вместо V ₁ , S ₁ ; V ₂ , S ₂ можно подставить их выражения через t ₁ и t ₂. В результате преобразований получим:

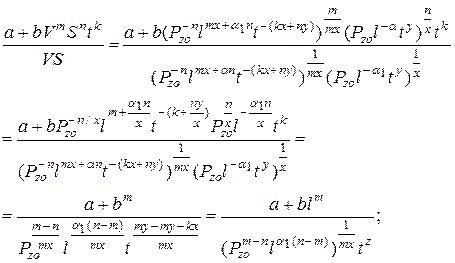
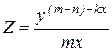
    Целевая функция примет вид:

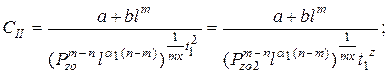
Учитывая ограничение на общий припуск t ₁ + t ₂ = и, можно сформировать следующую математическую модель оптимизации двухпроходной обработки:

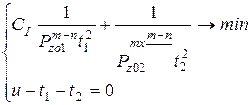
Функция Лагранжа будет иметь вид:

F = C + λ ( u – t ₁ t ₂ )

    Тогда оптимальные глубины решения найдутся как решения системы уравнений.

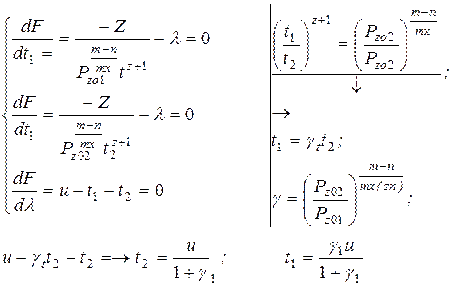
    Проанализируем зависимость себестоимости двухпроходной обработки от глубины резани на первом переходе. Для этого возьмем вторую производную от функции

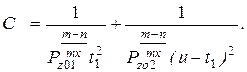
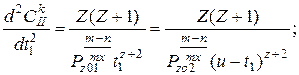
Из этого уравнения видно, что если Z ( Z+1)>0, то стационарная точка 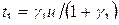является точкой минимума. Если Z ( Z+1)<0, то стационарная точка является точкой максимум. В последнем случае ввиду отсутствия других стационарных точек минимум будем искать на границе допустимых значений. Здесь необходимо рассмотреть и сравнить два варианта: t ₁ = t_{do п} , t ₂ = u – t_{do п} и t ₂ = t_{do п} , t ₁ = u – t_{do п}   Себестоимость первого варианта меньше, чем себестоимость второго, если выполняется неравенство

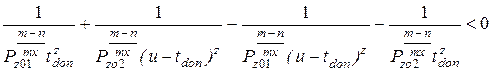
После преобразований получим

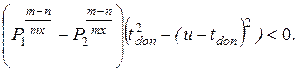
    Так как P ₁ > P ₂ , t_don > ( u – t_don ) Z < 0, то указанное неравенство выполняется всегда.

    Практический вывод из проведенного анализа следующий: если при двухпроходной обработке активными являются силовые ограничения и Z ( Z + 1) > 0, то глубина резания на проходе рассчитывается по формуле 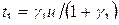; если, Z ( Z + 1) < 0 то глубина резания t ₁ на первом проходе принимается максимально допустимой из технологических соображений.

    Рассмотрим случай, когда активными на первом и втором проходе являются ограничения типа S₁ ≤ S_1max , S₂ ≤ S_2max. Тогда целевая функция примет вид

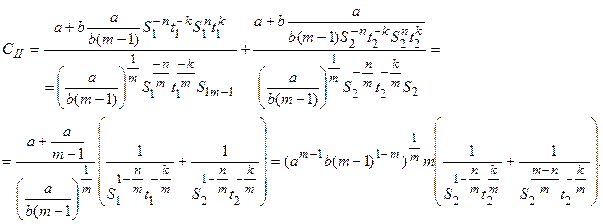Учитывая ограничение t ₁ + t ₂ = u и используя метод множителей Лагранжа, получим следующие выражения для определения оптимальных глубин резания на проходах:

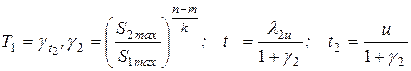
    Определим характер полученного экстремума целевой функции. Для этого возьмем вторую производную от функции

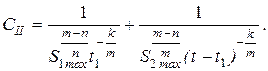
    Из этого уравнения видно, что если 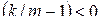 то стационарная точка является точкой максимум. В теории резания металлов утверждается, что. Таким образом, полученное решение задачи оптимального распределения припуска приводит к минимуму себестоимости.

    Так как целевая функция унимодальная, то будем искать решение задачи на границе области допустимых значений.

Рассмотрим два альтернативных варианта: t ₁ = t_lon , t ₂ = u = t_don и t ₁ = u = t_don ; t ₂ = t_lon ,   

Первый вариант предпочтительнее, если выполняется неравенство

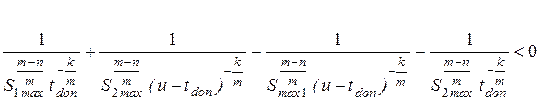
После преобразований получим

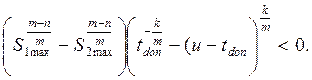
    Так как S _{1 max} > S _{2 max} , m > n k > m >0, t_don ( u – t_don ), то полученное неравенство выполняется всегда. Следовательно, при активных ограничениях типа S ₁ < S _{1 max}  , S _{2 max} ≤ S _{2 max}  необходимо на первом проходе назначить максимально возможную глубину резания.

    Рассмотрим вариант, когда на первом проходе активно силовое ограничение, а на втором – ограничение типа S ≤ S_max.

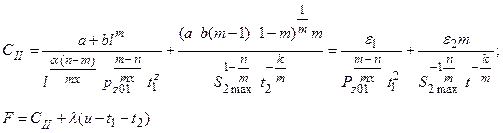
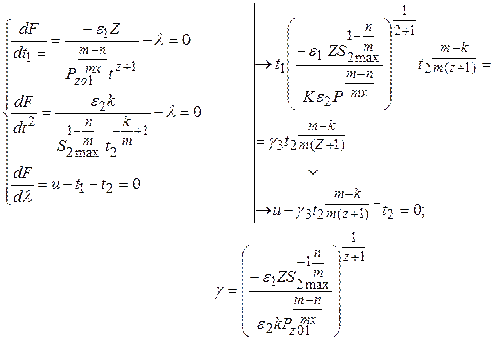
Полученное уравнение можно решить численным методом, используя стандартные программы резания уравнений типа f ( x ) = 0.

Проверим, является ли найденная стационарная точка минимумом целевой функции. Возьмем вторую производную от функции

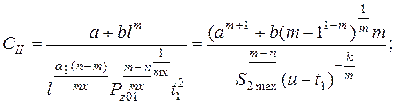
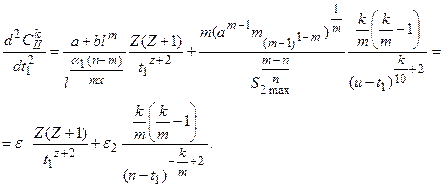
    Так как 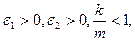 то при Z ( Z +1)< 0 стационарная точка является максимум. При Z ( Z +1)> 0    требуется оценивать разность между первым и вторым слагаемым. Если разность будет положительна, стационарная точка является точкой минимума. Если разность будет отрицательна, то стационарная точка является точкой максимума. Можно предположить, что и в этом случае оптимальной глубиной резания на первом походе будет предельно допустимая величина.

    Следует помнить, что двухпроходная обработка может быть экономичной, чем однопроходн. Такие условия могут возникнуть, например, когда требуется получить поверхность с низкой степенью шероховатости. При большой глубине резания это может привести к достаточно малому значению произведения VS, что вызовет рост себестоимости. Используя обработку за два прохода, можно значительно снизить себестоимость. Обработка за два прохода может быть экономичней обработки за один проход, когда станок имеет малую мощность привода главного движения.

ВОПРСЫ ДЛЯ САМОПРОВЕРКИ

1. Каков критерий оптимальности при оптимизации методом Лагранжа?

2. В чем заключается суть оптимизации режимов резания методом Лагранжа?

3. Как строится математическая модель оптимизации для метода Лагранжа?

4. В чем отличие МГП и МЛП от метода Лагранжа?

5. Каковы ограничения при решении задач оптимизации черновой обработки?

6. Каковы ограничения при решении задач оптимизации чистовой обработки?

7. Каков порядок расчетов оптимальных режимов резания методом Лагранжа?

8. В каких случаях двухпроходная обработка более экономична, чем однопроходная?

СТОХАСТИЧЕСКАЯ ОПТИМИЗАЦИЯ УРОВНЯ КАЧЕСТВА

РЕЖУЩЕГО ИНСТРУМЕНТА И РЕЖИМОВ РЕЗАНИЯ

Лекция 15. Представления о качестве инструмента как системы случайных величин

1. Система показателей качества режущего инструмента

2. Учет случайного характера критерия оптимальности и

основных показателей качества режущего инстумента