Наиболее распространенными я являются критерии максимальной производительности П и минимальной себестоимости С обработки. Основным параметром однопараметрической оптимизации режимов резания является скорость резания V_опт, причем наиболее целесообразно сначала определять оптимальный период стойкости инструмента Т_опт, а затем рассчитывать соответствующую ему оптимальную скорость.

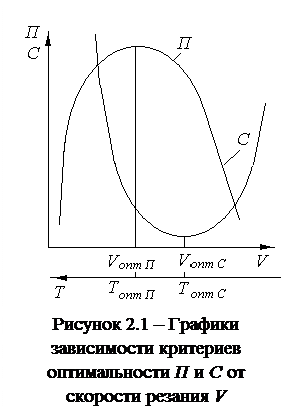Графики зависимости критериев оптимальности П и С от скорости резания V периода стойкости Т представлены на рис.2.1. Известно, что с увеличением скорости резания производительность обработки увеличивается, однако при этом растет и интенсивность изнашивания, в связи с чем, снижается стойкость, возрастает частота и общее время смен инструмента и, вследствие чего производительность начинает уменьшаться. Наибольшая производительность достигается при определенном уровне скорости резания и соответствующей ей стойкости, называемых оптимальными по производительности V_{опт П}. и Т_{опт П}.

Себестоимость обработки с увеличением скорости резания и соответствующим ростом производительности снижается до определенного уровня, а затем в связи с увеличением затрат на смену инструмента начинает возрастать. Наименьшая себестоимость достигается при определенном уровне скорости резания и соответствующей ей стойкости, называемых оптимальными по себестоимости V_{опт С}. и Т_{опт С}.

Производительность обработки обратно пропорциональна затрачиваемому на нее времени. В качестве критерия оптимизации используется переменная часть штучно-калькуляционного времени, зависящего от режимов резания:

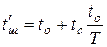,                                             (2.1)

где t_o- основное время обработки; t_c - время смены инструмента; T - период стойкости инструмента.

Основное время обработки:

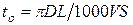,                                                    (2.2)

где D- диаметр обрабатываемой поверхности; L – длина; V – скорость резания; S – подача.

Скорость резания:

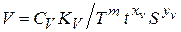,                                     (2.3)

где C _V, K _V – коэффициенты и  x_v, y _v, m _v – показатели, которые характеризуют степень влияния глубины t, подачи S и стойкости T на скорость резания V, определяемые в зависимости от условий эксплуатации.

Подставляя (2) и (3) в выражение (1), получаем:

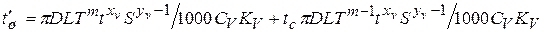. (2.4)

Полученное выражение может быть выражено через переменный параметр Т – период стойкости следующим образом:

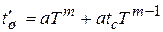,                                        (2.5)

где 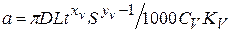 – постоянный коэффициент.

Оптимальный период стойкости, обеспечивающий минимум штучно-калькуляционного времени или максимум производительности, определяется из уравнений:

;

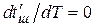;                                                    (2.6)

;

.

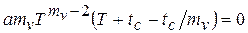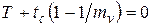Оптимальный по производительности период стойкости равен:

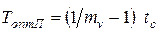.                                    (2.7)

Из полученного выражения следует, что оптимальный по производительности период стойкости зависит только от показателя относительной стойкости m_v и времени смены инструмента t_c и не зависит от других условий обработки, связанных с характеристиками оборудования, оснастки, инструмента и детали.

Повышению производительности может способствовать повышение быстросменности инструмента (снижение времени смены t_c), например, использование инструмента с механическим креплением сменных режущих пластин. В этом случае оптимальный период стойкости снижается, а оптимальная скорость резания и производительность возрастают.

Оптимальная по производительности скорость резания равна:

.                                 (2.8)
2 Оптимизация стойкости по критерию минимальной себестоимости

При оптимизации режимов резания по критерию минимальной себестоимости обработки и качестве критерия оптимизации используется переменная часть себестоимости, зависящая от режимов резания:

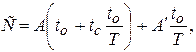                                 (2.9)

где А - себестоимость станко-минуты; А' - стоимость инструмента, приведенная к одному периоду стойкости.

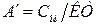,                                            (2.10)

где С_и – стоимость инструмента, К - количество периодов стойкости (для напайного инструмента К = п_р+1, где п_р - количество переточек; для инструмента с многогранными перетачиваемыми К = mN, где m – количество режущих граней пластины, N - количество пластин, выдерживаемых одной державкой). n - частота вращения детали D – диаметр обработки,

По аналогии с (2.5) выражение (2.9) может быть выражено через переменный параметр Т – период стойкости следующим образом:

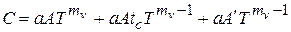.                           (2.11)

Оптимальный период стойкости, обеспечивающий минимум себестоимости, определяемый из уравнения 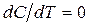, равен:

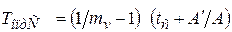.                                    (2.12)

Из полученного выражения следует, что оптимальная по себестоимости стойкость зависит от показателя относительной стойкости m_v и времени смены инструмента t_c, а также соотношения стоимостей одной минуты работы инструмента и оборудования А'/А.

Оптимальный по себестоимости период стойкости всегда больше, чем по производительности. Оптимальный по себестоимости период стойкости возрастает пропорционально времени смены t_c и соотношению стоимостей одной минуты работы инструмента и оборудования А'/А. то является увеличению стоимости инструмента и снижению стоимости станкоминуты.

Снижению себестоимости обработки будут способствовать наряду с повышением быстросменности инструмента, снижение стоимости одной минуты работы инструмента, как за счет снижения стоимости самого инструмента, так и за счет роста его долговечности. Использование современного оборудования, в том числе с числовым программным управлением, с более высокой стоимостью эксплуатации оборудования, то является с большей стоимостью станкоминуты, также приводит к необходимости снижения оптимального периода стойкости, что обеспечит и снижение себестоимости обработки.

Оптимальная по себестоимости скорость резания равна:

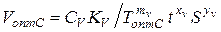.                                 (2.13)

Лекция 3. Формирование системы ограничений при механообработке

1. Ограничения при расчете режимов резания

2. Математическая модель процесса резания